Математическая лингвистика (original) (raw)
Математи́ческая лингви́стика —
математическая дисциплина, предметом которой является разработка формального аппарата для описания строения естественных и некоторых искусственных языков. Возникла в 50‑х гг. 20 в.; одним из главных стимулов появления М. л. послужила назревшая в языкознании потребность уточнения его основных понятий. Методы М. л. имеют много общего с методами математической логики — математической дисциплины, занимающейся изучением строения математических рассуждений, — и в особенности таких её разделов, как теория алгоритмов и теория автоматов. Широко используются в М. л. также алгебраические методы. М. л. развивается в тесном взаимодействии с языкознанием. Иногда термин «М. л.» используется также для обозначения любых лингвистических исследований, в которых применяется какой-либо математический аппарат.
Математическое описание языка основано на восходящем к Ф. де Соссюру представлении о языке как механизме, функционирование которого проявляется в речевой деятельности его носителей; её результатом являются «правильные тексты» — последовательности речевых единиц, подчиняющиеся определённым закономерностям, многие из которых допускают математическое описание. Разработка и изучение способов математического описания правильных текстов (в первую очередь предложений) составляет содержание одного из разделов М. л. — теории способов описания синтаксической структуры. Для описания строения предложения — точнее, его синтаксической структуры — можно либо выделить в нём составляющие — группы слов, функционирующие как цельные синтаксические единицы, либо указать для каждого слова те слова, которые ему непосредственно подчинены (если такие есть). Так, в предложении «Ямщик сидит на облучке» (А. С. Пушкин) при описании по 1‑му способу составляющими будут все предложение П, каждое его отдельное слово и группы слов A = сидит на облучке и B = на облучке (см. рис. 1; стрелки означают «непосредственное вложение»); описание по 2‑му способу даёт схему, показанную на рис. 2. Возникающие при этом математические объекты называются системой составляющих (1‑й способ) и деревом синтаксического подчинения (2‑й способ).
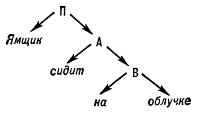
Рис. 1
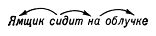
Рис. 2
Точнее, система составляющих — это множество отрезков предложения, содержащее в качестве элементов всё предложение и все вхождения слов в это предложение («однословные отрезки») и обладающее тем свойством, что каждые два входящих в него отрезка либо не пересекаются, либо один из них содержится в другом; дерево синтаксического подчинения, или просто дерево подчинения, есть дерево, множеством узлов которого служит множество вхождений слов в предложение.Деревом в математике называется множество, между элементами которого — их называют узлами — установлено бинарное отношение — его называют отношением подчинения и графически изображают стрелками, идущими от подчиняющих узлов к подчиненным, — такое, что: 1) среди узлов имеется точно один — его называют_корнем_, — не подчинённый никакому узлу; 2) каждый из остальных узлов подчинен точно одному узлу; 3) невозможно, отправившись из какого-либо узла вдоль стрелок, вернуться в тот же узел. Узлы дерева подчинения — это вхождения слов в предложения. При графическом изображении система составляющих (как на рис. 1) также приобретает вид дерева (дерева составляющих). Построенное для предложения дерево подчинения или систему составляющих часто называют его_синтаксической структурой_ в виде дерева подчинения (системы составляющих). Системы составляющих используются преимущественно в описаниях языков с жёстким порядком слов, деревья подчинения — в описаниях языков со свободным порядком слов (в частности, русского), формально для каждого (не слишком короткого) предложения можно построить много разных синтаксических структур любого из двух видов, но среди них только одна или несколько являются правильными. Корнем правильного дерева подчинения служит обычно сказуемое. Предложение, имеющее более одной правильной синтаксической структуры (одного вида), называется синтаксически омонимичным; как правило, разные синтаксические структуры отвечают разным смыслам предложения. Например, предложение «Школьники из Ржева поехали в Торжок» допускает два правильных дерева подчинения (рис. 3, а, б); первое из них отвечает смыслу «Ржевские школьники поехали (не обязательно из Ржева) в Торжок», второе — «Школьники (не обязательно ржевские) поехали из Ржева в Торжок».
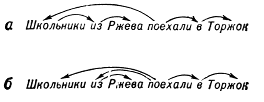
Рис. 3
В русском и ряде других языков деревья подчинения предложений «делового стиля» подчиняются, как правило, закону проективности, состоящему в том, что все стрелки можно провести над прямой, на которой записано предложение, таким образом, что никакие две из них не пересекутся и корень не будет лежать ни под какой стрелкой. В языке художественной литературы, особенно в поэзии, отклонения от закона проективности допустимы и чаще всего служат задаче создания определённого художественного эффекта. Так, в предложении «Друзья кровавой старины народной чаяли войны» (Пушкин) непроективность приводит к эмфатическомувыделению слова «народной» и одновременно как бы замедляет речь, создавая этим впечатление известной приподнятости, торжественности. Имеются и другие формальные признаки деревьев подчинения, которые могут использоваться для характеризации стиля. Например, максимальное число вложенных друг в друга стрелок служит мерой «синтаксической громоздкости» предложения (см. рис. 4).

Рис. 4
Для более адекватного описания строения предложения составляющие обычно помечаются символами грамматических категорий («именная группа», «группа переходного глагола» и т. п.), а стрелки дерева подчинения — символами синтаксических отношений («предикативное», «определительное» и т. п.).
Аппарат деревьев подчинения и систем составляющих используется также для представления глубинно-синтаксической структуры предложения, которая образует промежуточный уровень между семантической и обычной синтаксической структурой (последнюю часто называют поверхностно-синтаксической).
Более совершенное представление синтаксической структуры предложения (требующее, однако, более сложного математического аппарата) дают_системы синтаксических групп_, в которые входят как словосочетания, так и синтаксические связи, причём не только между словами, но и между словосочетаниями. Системы синтаксических групп позволяют совмещать строгость формального описания строения предложения с гибкостью, присущей традиционным, неформальным описаниям. Деревья подчинения и системы составляющих являются предельными частными случаями систем синтаксических групп.
Другой раздел М. л., занимающий в ней центральное место, — теория формальных грамматик, начало которой было положено работами Н. Хомского. Она изучает способы описания закономерностей, характеризующих уже не отдельный текст, а всю совокупность правильных текстов того или иного языка. Эти закономерности описываются с помощью_формальной грамматики_ — абстрактного «механизма», позволяющего с помощью единообразной процедуры получать правильные тексты данного языка вместе с описаниями их структуры. Наиболее широко используемый тип формальной грамматики — порождающая грамматика, или грамматика Хомского, представляющая собой упорядоченную систему Г = ⟨ V, W, П, R ⟩, где V и W — непересекающиеся конечные множества, называемые соответственно основным, или терминальным, и_вспомогательным_, или нетерминальным,алфавитами (их элементы называются соответственно основными, или терминальными, и вспомогательными, или нетерминальными,символами), П — элемент W, называемый начальным символом, и R — конечное множество правил вида φ → ψ, где φ и ψ — цепочки (конечные последовательности) из основных и вспомогательных символов. Если φ → ψ — правило грамматики Г и ω1, ω2 — цепочки из основных и вспомогательных символов, говорят, что цепочка ω1ψω2 непосредственно выводима в Г из ω1φω2. Если ξ0, ξ1, ..., ξn — цепочки и для каждого i = 1, ..., n цепочка ξi непосредственно выводима из ξi−1, говорят, что ξn выводима в Г из ξ0. Множество тех цепочек из основных символов, которые выводимы в Г из её начального символа, называется языком, порождаемым грамматикой Г, и обозначается L(Г). Если все правила Г имеют вид η1Aη2 → η1ωη2, то Г называется грамматикой составляющих (или непосредственно составляющих), сокращённо НС-грамматикой; если при этом в каждом правиле цепочки η1 и η2 (правый и левый контексты) пусты, то грамматика называется бесконтекстной (или_контекстно-свободной_), сокращённо Б-грамматикой (или КС-грамматикой). В наиболее обычной лингвистической интерпретации основные символы представляют собой слова, вспомогательные — символы грамматических категорий, начальный символ — символ категории «предложение»; при этом язык, порождаемый грамматикой, интерпретируется как множество всех грамматически правильных предложений данного естественного языка. В НС-грамматике вывод предложения даёт для неё дерево составляющих, в котором каждая составляющая состоит из слов, «происходящих» от одного вспомогательного символа, так что для каждой составляющей указывается её грамматическая категория. Так, если грамматика имеет, в числе прочих, правила П → Sx, y, им, Vy → ViyO, O → Sx, y, предл, Viy → сидит, Sмуж, ед., им → на, ямщик, Sмуж, ед., предл. → облучке, то предложение «Ямщик сидит на облучке» имеет вывод, показанный на рис. 5, где стрелки идут от левых частей применяемых правил к элементам правых частей. Система составляющих, отвечающая этому выводу, совпадает с изображенной на рис. 1. Возможны и другие интерпретации: например, основные символы могут интерпретироваться как морфы, вспомогательные — как символы типов морф и допустимых цепочек морф, начальный символ — как символ типа «словоформа», а язык, порождаемый грамматикой, — как множество правильных словоформ (морфологическая интерпретация); употребительны также морфонологическая и фонологическая интерпретации. В реальных описаниях языков используются обычно «многоуровневые» грамматики, которые содержат последовательно работающие синтаксические, морфологические и морфонологически-фонологические правила.
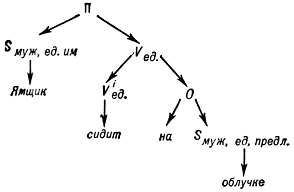
Рис. 5
Другой важный тип формальной грамматики — доминационная грамматика, которая порождает множество цепочек, интерпретируемых обычно как предложения вместе с их синтаксическими структурами в виде деревьев подчинения. Грамматика синтаксических групп порождает множество предложений вместе с их синтаксическими структурами, имеющими вид систем синтаксических групп. Имеются также различные концепции трансформационнойграмматики (грамматики деревьев), служащей не для порождения предложений, а для преобразования деревьев, интерпретируемых как деревья подчинения или деревья составляющих. Примером может служить Δ-грамматика — система правил преобразования деревьев, интерпретируемых как «чистые» деревья подчинения предложений, т. е. деревья подчинения без линейного порядка слов.
Особняком стоят грамматики Монтегю, служащие для одновременного описания синтаксических и семантических структур предложения; в них используется сложный математико-логический аппарат (так называемая интенсиональная логика).
Формальные грамматики находят применение для описания не только естественных, но и искусственных языков, в особенности языков программирования.
В М. л. разрабатываются также аналитические модели языка, в которых на основе тех или иных данных о речи, считающихся известными, производятся формальные построения, результатом которых является описание некоторых аспектов строения языка. В этих моделях обычно используется несложный математический аппарат — простые понятия теории множеств и алгебры; поэтому аналитические модели языка иногда называют_теоретико-множественными_. В аналитических моделях наиболее простого типа исходными данными служат множество правильных предложений и система окрестностей — совокупностей «слов», принадлежащих одной лексеме (например, {дом, до́ма, дому, домом, доме, дома́, домов, домам, домами, домах}). Простейшим производным понятием в таких моделях является замещаемость: слово a замещаемо на слово b, если всякое правильное предложение, содержащее вхождение слова a, остаётся правильным при замене этого вхождения вхождением слова b. Если а замещаемо на b и_b_ на a, говорят, что a и b взаимозамещаемы. (Например, в русском языке слово «синий» замещаемо на слово «голубой»; слова «синего» и «голубого» взаимозамещаемы.) Класс слов, взаимозамещаемых между собой, называется_семейством_. Исходя из окрестностей и семейств, можно получить ряд других лингвистически значимых классификаций слов, одна из которых приблизительно соответствует традиционной системе частей речи. В другом типе аналитических моделей вместо множества правильных предложений используется отношение потенциального подчинения между словами, означающее способность одного из них подчинять себе другое в правильных предложениях. В таких моделях можно получить, в частности, формальные определения ряда традиционных грамматических категорий — например, формальное определение падежа существительного, представляющее собой процедуру, которая позволяет восстановить падежную систему языка, зная только отношение потенциального подчинения, систему окрестностей и множество слов, являющихся формами существительных.
В аналитических моделях языка используются простые понятия теории множеств и алгебры. К аналитическим моделям языка близки дешифровочные модели — процедуры, позволяющие по достаточно большому корпусу текстов на неизвестном языке без каких-либо предварительных сведений о нём получить ряд данных о его структуре.
По своему назначению М. л. является прежде всего инструментом теоретического языковедения. В то же время ее методы находят широкое применение в прикладных лингвистических исследованиях — автоматической обработке текста, автоматическом переводе и разработках, связанных с так называемым общением между человеком и ЭВМ.
- Кулагина О. С., Об одном способе определения грамматических понятий на базе теории множеств, в сб.: Проблемы кибернетики, в. 1, М., 1958;
- Хомский Н., Синтаксические структуры, в сб.: «Новое в лингвистике», в. 2, М., 1962;
- Гладкий А. В., Мельчук И. А., Элементы математической лингвистики, М., 1969 (лит.);
- их же, Грамматики деревьев, I, II, в сб.: Информационные вопросы семиотики, лингвистики и автоматического перевода, в. 1, 4, М., 1971—74 (лит.);
- Маркус С., Теоретико-множественные модели языков, пер. с англ., М., 1970 (лит.);
- Гладкий А. В., Формальные грамматики и языки, М., 1973 (лит.);
- его же, Попытка формального определения понятий падежа и рода существительного, в сб.: Проблемы грамматического моделирования, М., 1973 (лит.);
- его же, Синтаксические структуры естественного языка в автоматизированных системах общения, М., 1985 (лит.);
- Сухотин Б. В., Оптимизационные методы исследования языка. М., 1976 (лит.);
- Севбо И. П., Графическое представление синтаксических структур и стилистическая диагностика, К., 1981;
- Парти Б. Х., Грамматика Монтегю, мысленные представления и реальность, в кн.: Семиотика, М., 1983;
- Montague R., Formal philosophy, New Haven — L., 1974 (лит.).
А. В. Гладкий.