plotAdded - Added variable plot of linear regression model - MATLAB (original) (raw)

Added variable plot of linear regression model

Syntax

Description

plotAdded([mdl](#bsz4c96-1%5Fsep%5Fshared-mdl),[coef](#bsz4c96-1-coef)) creates an added variable plot for the specified termscoef.

example

plotAdded([mdl](#bsz4c96-1%5Fsep%5Fshared-mdl),[coef](#bsz4c96-1-coef),[Name,Value](#namevaluepairarguments)) specifies graphical properties of adjusted data points using one or more name-value pair arguments. For example, you can specify the marker symbol and size for the data points.

plotAdded([ax](#bsz4c96-1%5Fsep%5Fshared-ax),___) creates the plot in the axes specified by ax instead of the current axes, using any of the input argument combinations in the previous syntaxes.

[h](#mw%5F12f28e3e-e057-4020-b5cc-571bb9586b0e) = plotAdded(___) returns line objects for the plot. Use h to modify the properties of a specific line after you create the plot. For a list of properties, see Line Properties.

Examples

collapse all

Create a linear regression model of car mileage as a function of weight and model year. Then create an added variable plot to see the significance of the model.

Create a linear regression model of mileage from the carsmall data set.

load carsmall Year = categorical(Model_Year); tbl = table(MPG,Weight,Year); mdl = fitlm(tbl,'MPG ~ Year + Weight^2');

Create an added variable plot of the model.

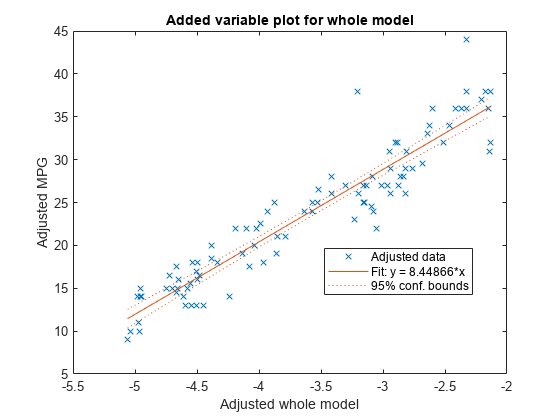
Figure contains an axes object. The axes object with title Added Variable Plot for Whole Model, xlabel Adjusted Whole Model, ylabel Adjusted MPG contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent Adjusted data, Fit: y = 8.44866*x, 95% conf. bounds.

The plot illustrates that the model is significant because a horizontal line does not fit between the confidence bounds.

Create the same plot by using the plotAdded function.

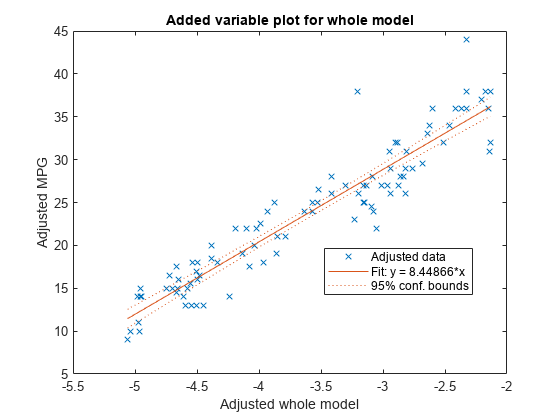
Create a linear regression model of car mileage as a function of weight and model year. Then create an added variable plot to see the effect of the weight terms (Weight and Weight^2).

Create the linear regression model using the carsmall data set.

load carsmall Year = categorical(Model_Year); tbl = table(MPG,Weight,Year); mdl = fitlm(tbl,'MPG ~ Year + Weight^2');

Find the terms in the model corresponding to Weight and Weight^2.

ans = 1×5 cell {'(Intercept)'} {'Weight'} {'Year_76'} {'Year_82'} {'Weight^2'}

The weight terms are 2 and 5.

Create an added variable plot with the weight terms.

coef = [2 5]; plotAdded(mdl,coef)

Figure contains an axes object. The axes object with title Added Variable Plot for Specified Terms, xlabel Adjusted Specified Terms, ylabel Adjusted MPG contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent Adjusted data, Fit: y = 0.0164036*x, 95% conf. bounds.

The plot illustrates that the weight terms are significant because a horizontal line does not fit between the confidence bounds.

Create a scatter plot of data along with a fitted curve and confidence bounds for a simple linear regression model. A simple linear regression model includes only one predictor variable.

Create a simple linear regression model of mileage from the carsmall data set.

load carsmall tbl = table(MPG,Weight); mdl = fitlm(tbl,'MPG ~ Weight')

mdl = Linear regression model: MPG ~ 1 + Weight

Estimated Coefficients: Estimate SE tStat pValue
__________ _________ _______ __________

(Intercept)        49.238       1.6411     30.002    2.7015e-49
Weight         -0.0086119    0.0005348    -16.103    1.6434e-28

Number of observations: 94, Error degrees of freedom: 92 Root Mean Squared Error: 4.13 R-squared: 0.738, Adjusted R-Squared: 0.735 F-statistic vs. constant model: 259, p-value = 1.64e-28

pValue of the Weight variable is very small, which means that the variable is statistically significant in the model. Visualize this result by creating a scatter plot of the data, along with a fitted curve and its 95% confidence bounds, using the plot function.

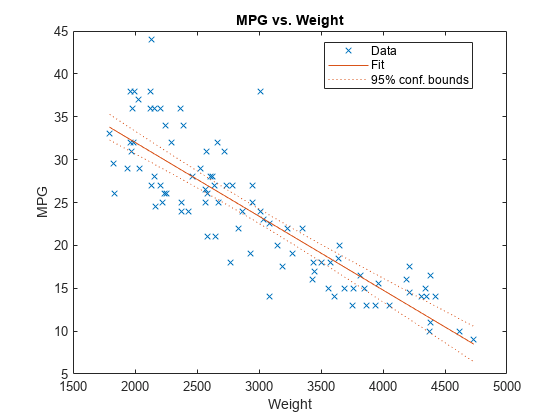
Figure contains an axes object. The axes object with title MPG vs. Weight, xlabel Weight, ylabel MPG contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent Data, Fit, 95% conf. bounds.

The plot illustrates that the model is significant because a horizontal line does not fit between the confidence bounds, which is consistent with the pValue result.

Create the same plot by using the plotAdded function.

Figure contains an axes object. The axes object with title Added Variable Plot for Weight, xlabel Adjusted Weight, ylabel Adjusted MPG contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent Adjusted data, Fit: y = -0.00861193*x, 95% conf. bounds.

When a model includes only one term in addition to the constant term, an adjusted value is equivalent to its original value. Therefore, this added variable plot is the same as the scatter plot created by the plot function.

Input Arguments

collapse all

Coefficients in the regression model mdl, specified as one of the following:

Character vector or string scalar of a single coefficient name inmdl.CoefficientNames (CoefficientNames property ofmdl).
Vector of positive integers representing the indexes of coefficients in mdl.CoefficientNames. Use a vector to specify multiple coefficients.

Data Types: char | string | single | double

Name-Value Arguments

collapse all

Specify optional pairs of arguments asName1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'Color','blue','Marker','*'

Note

The graphical properties listed here are only a subset. For a complete list, see Line Properties. The specified properties determine the appearance of adjusted data points.

Line color, specified an RGB triplet, hexadecimal color code, color name, or short name for one of the color options listed in the following table.

The Color name-value argument also determines marker outline color and marker fill color if MarkerEdgeColor is"auto" (default) and MarkerFaceColor is"auto".

For a custom color, specify an RGB triplet or a hexadecimal color code.

An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range [0,1], for example, [0.4 0.6 0.7].
A hexadecimal color code is a string scalar or character vector that starts with a hash symbol (#) followed by three or six hexadecimal digits, which can range from 0 to F. The values are not case sensitive. Therefore, the color codes"#FF8800","#ff8800","#F80", and"#f80" are equivalent.

Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and the hexadecimal color codes.

Color Name	Short Name	RGB Triplet	Hexadecimal Color Code	Appearance
"red"	"r"	[1 0 0]	"#FF0000"
"green"	"g"	[0 1 0]	"#00FF00"
"blue"	"b"	[0 0 1]	"#0000FF"
"cyan"	"c"	[0 1 1]	"#00FFFF"
"magenta"	"m"	[1 0 1]	"#FF00FF"
"yellow"	"y"	[1 1 0]	"#FFFF00"
"black"	"k"	[0 0 0]	"#000000"
"white"	"w"	[1 1 1]	"#FFFFFF"
"none"	Not applicable	Not applicable	Not applicable	No color

This table lists the default color palettes for plots in the light and dark themes.

Palette	Palette Colors
"gem" — Light theme default_Before R2025a: Most plots use these colors by default._
"glow" — Dark theme default

You can get the RGB triplets and hexadecimal color codes for these palettes using the orderedcolors and rgb2hex functions. For example, get the RGB triplets for the "gem" palette and convert them to hexadecimal color codes.

RGB = orderedcolors("gem"); H = rgb2hex(RGB);

Before R2023b: Get the RGB triplets using RGB = get(groot,"FactoryAxesColorOrder").

Before R2024a: Get the hexadecimal color codes using H = compose("#%02X%02X%02X",round(RGB*255)).

Example: Color="blue"

Data Types: single | double | string | char

Line width, specified as a positive value in points. If the line has markers, then the line width also affects the marker edges.

Example: LineWidth=0.75

Data Types: single | double

Marker symbol, specified as one of the values in this table.

Marker	Description	Resulting Marker
"o"	Circle
"+"	Plus sign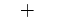
"*"	Asterisk
"."	Point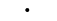
"x"	Cross
"_"	Horizontal line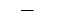
"\|"	Vertical line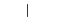
"square"	Square
"diamond"	Diamond
"^"	Upward-pointing triangle
"v"	Downward-pointing triangle
">"	Right-pointing triangle
"<"	Left-pointing triangle
"pentagram"	Pentagram
"hexagram"	Hexagram
"none"	No markers	Not applicable

Example: Marker="+"

Data Types: string | char

Marker outline color, specified an RGB triplet, hexadecimal color code, color name, or short name for one of the color options listed in theColor name-value argument.

The default value "auto" uses the same color specified by using the Color name-value argument. You can also specify"none" for no color.

Example: MarkerEdgeColor="blue"

Data Types: single | double | string | char

Marker fill color, specified as an RGB triplet, hexadecimal color code, color name, or short name for one of the color options listed in the Color name-value argument. The default value "none" specifies no color.

The "auto" value uses the same color specified by using theColor name-value argument.

Example: MarkerFaceColor="blue"

Data Types: single | double | string | char

Marker size, specified as a positive value in points.

Example: MarkerSize=2

Data Types: single | double

Output Arguments

collapse all

Line objects, returned as a 3-by-1 vector. h(1),h(2), and h(3) correspond to the adjusted data points, fitted line, and 95% confidence bounds of the fitted line, respectively. Use dot notation to query and set properties of the line objects. For details, see Line Properties.

You can use name-value pair arguments to specify the appearance of adjusted data points corresponding to the first graphics objecth(1).

More About

collapse all

An added variable plot, also known as a partial regression leverage plot, illustrates the incremental effect on the response of specified terms caused by removing the effects of all other terms.

An added variable plot created by plotAdded with a single selected term corresponding to a single predictor variable includes these plots:

Scatter plot of adjusted response values against adjusted predictor variable values
Fitted line for adjusted response values as a function of adjusted predictor variable values
95% confidence bounds of the fitted line

The adjusted values are equal to the average of the variable plus the residuals of the variable fit to all predictors except the selected predictor. For example, consider an added variable plot for the first predictor variable_x_1. Fit the response variable_y_ and the selected predictor variable_x_1 to all predictors except_x_1 as follows:

yi =gy(x_2_i,x_3_i, …,xpi) +ryi,

x_1_i =gx(x_2_i,x_3_i, …,xpi) +rxi,

where gy and_gx_ are the fit of y and_x_1, respectively, against all predictors except the selected predictor (x_1).ry and_rx are the corresponding residual vectors. The subscript i represents the observation number. The adjusted value is the sum of the average value and the residual for each observation.

where x¯1 and y¯ represent the average of x_1 and_y, respectively.

plotAdded plots a scatter plot of (x˜1i, y˜i), a fitted line for y˜ as a function of x˜1 (that is, β1x˜1), and the 95% confidence bounds of the fitted line. The coefficient_β_1 is the same as the coefficient estimate of_x_1 in the full model, which includes all predictors.

ryi represents the part of the response values unexplained by the predictors (except x_1), and_rxi represents the part of the_x_1 values unexplained by the other predictors. Therefore, the fitted line represents how the new information introduced by adding_x_1 can explain the unexplained part of the response values. If the slope of the fitted line is close to zero and the confidence bounds can include a horizontal line, then the plot indicates that the new information from_x_1 does not explain the unexplained part of the response values well. That is, _x_1 is not significant in the model fit.

plotAdded also supports an extension of the added variable plot so that you can select multiple terms instead of a single term. Therefore, you can also specify a categorical predictor, all terms that involve a specific predictor, or the model as a whole (except a constant (intercept) term). Consider a set of predictors X with a coefficient vector β, where_βi_ is the coefficient estimate of_xi_ in the full model if you specify the_i_th coefficient for an added variable plot; otherwise,βi is zero. Define a unit direction vector_u_ as u =β/s where s = norm(β). Then, X β = (X u)s. Treat X u as a single predictor with a coefficient s, and create an added variable plot for_X_ u in the same way as creating the plot for a single term. The coefficient of the fitted line in the added variable plot corresponds to_s_.

Tips

The data cursor displays the values of the selected plot point in a data tip (small text box located next to the data point). The data tip includes the _x_-axis and_y_-axis values for the selected point, along with the observation name or number.

Alternative Functionality

A LinearModel object provides multiple plotting functions.
- When creating a model, use plotAdded to understand the effect of adding or removing a predictor variable.
- When verifying a model, use plotDiagnostics to find questionable data and to understand the effect of each observation. Also, use plotResiduals to analyze the residuals of the model.
- After fitting a model, use plotAdjustedResponse, plotPartialDependence, and plotEffects to understand the effect of a particular predictor. UseplotInteraction to understand the interaction effect between two predictors. Also, use plotSlice to plot slices through the prediction surface.
plotAdded shows the incremental effect on the response of specified terms by removing the effects of the other terms, whereasplotAdjustedResponse shows the effect of a selected predictor in the model fit with the other predictors averaged out by averaging the fitted values. Note that the definitions of adjusted values in plotAdded andplotAdjustedResponse are not the same.

Extended Capabilities

Version History

Introduced in R2012a