Fabry–Pérot interferometers (original) (raw)
Definition: interferometers consisting of two highly reflecting mirrors, forming a standing-wave resonator
Alternative term: Fabry–Pérot resonators
- interferometers
- etalons
- common-path interferometers
- Fabry–Pérot interferometers
- Fizeau interferometers
- Gires–Tournois interferometers
- Mach–Zehnder interferometers
- Michelson interferometers
- Twyman–Green interferometers
- white light interferometers
- (more topics)
Related: Fabry–Perot laser diodesstanding-wave resonatorsinterferometersspectrometersetalonsGires–Tournois interferometerssupermirrorsoptical resonatorsresonator modesmode matchingreference cavitiesfree spectral range
Page views in 12 months: 7390
DOI: 10.61835/qrw Cite the article: BibTex BibLaTex plain textHTML Link to this page! LinkedIn
Content quality and neutrality are maintained according to our editorial policy.
📦 For purchasing Fabry–Pérot interferometers, use the RP Photonics Buyer's Guide — an expert-curated directory for finding all relevant suppliers, which also offers advanced purchasing assistance.
Contents
What is a Fabry–Pérot Interferometer?
A Fabry–Pérot interferometer (also called Fabry–Pérot resonator) is a linear optical resonator (or cavity) which consists of two highly reflecting mirrors (with some small transmissivity) and is often used as a high-resolution optical spectrometer. One exploits the fact that the transmission through such a resonator exhibits sharp resonances and is very small between those.
The spelling Fabry–Perot (without accent) is also frequently seen. Alfred Perot spelled his name with the accent, but the French civil register didn't.
Operation Principle
The following explanations, assuming a lossless symmetric high-finesse Fabry–Pérot, help to understand its operation principles:
- A substantial circulating optical power in the resonator is possible only if the input wave has an optical frequency close to one of the resonance frequencies of the resonator.
- In resonance, the contribution of the input wave leaking through the input mirror adds constructively to the circulating wave. And, there is destructive interference for the reflected field: the input field reflected at the input mirror is canceled by the field leaking out of the resonator. Therefore, there is effectively no reflection in resonance.
- In anti-resonance, the circulating field is quite weak, and most radiation is reflected at the input mirror. The weak field leaking out of the resonator towards the input source adds constructively to the reflected field.
Figure 1 shows the frequency-dependent transmittance in an example case, where we assume that all incident light is mode-matched to the fundamental spatial resonator mode:

Figure 1: Frequency-dependent transmission of a linear Fabry–Pérot cavity with mirror reflectivities of 90%.
The resonance frequencies can often be tuned by changing the cavity length (mirror distance) with a piezo actuator. When the voltage applied to the piezo is periodically varied, e.g. with a triangular temporal shape, and the transmitted power versus time is monitored with a photodetector and an oscilloscope, the latter can directly display the optical spectrum of the incident light, provided that the spectral width is smaller than the free spectral range and the scan is slow enough to reach a quasi-stationary state of the resonator.
The following animated diagrams show how the reflected and transmitted complex amplitudes evolve when the residence condition is tuned.
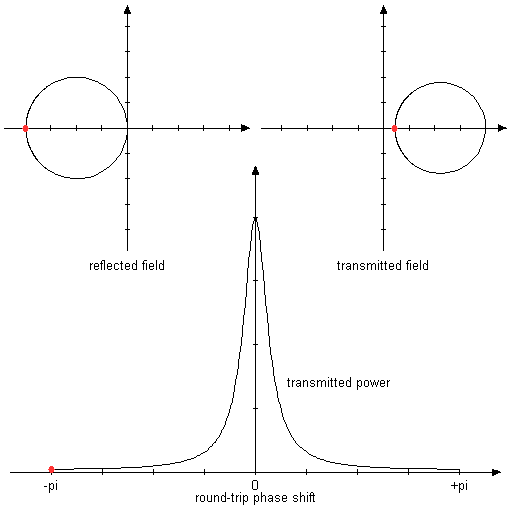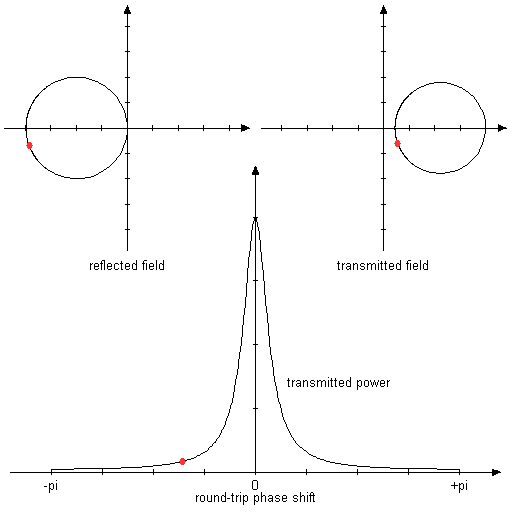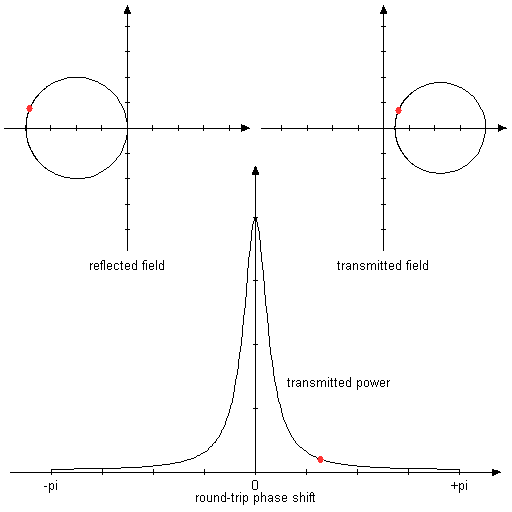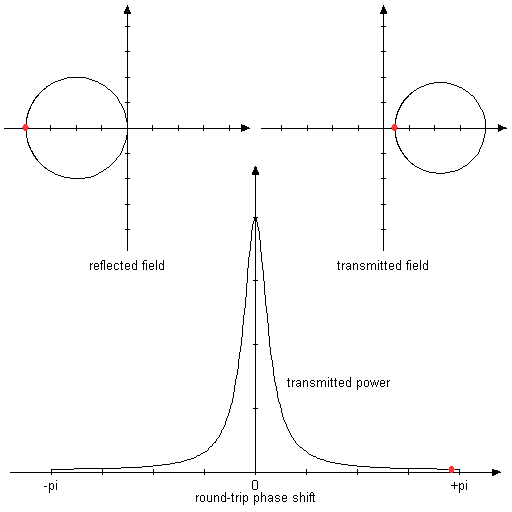
Figure 2: Animated graphs, showing the reflected and transmitted complex amplitudes and the power transmission while the round-trip phase shift is varied.
Both mirrors are assumed to have a reflectance of 80%. In this symmetric situation, total transmission and zero reflection are obtained in resonance.
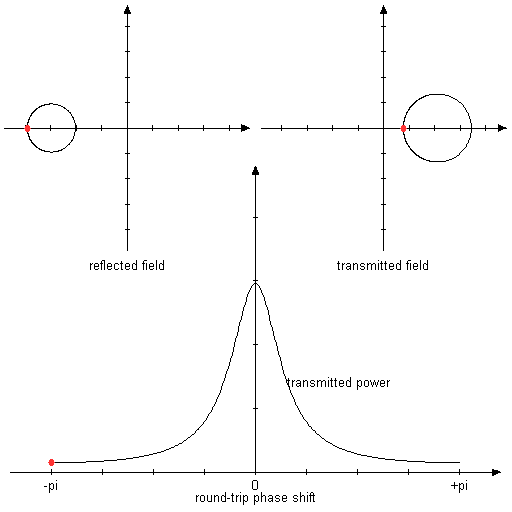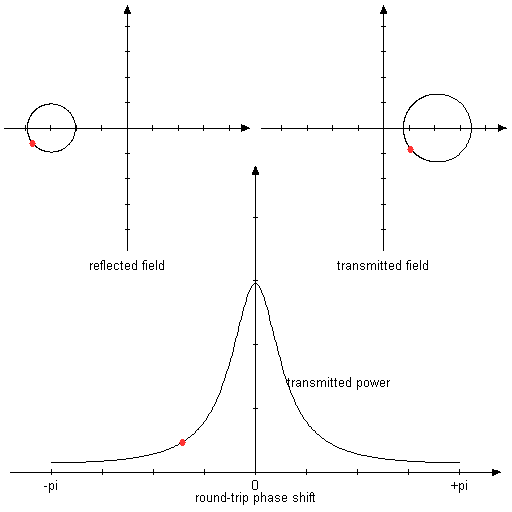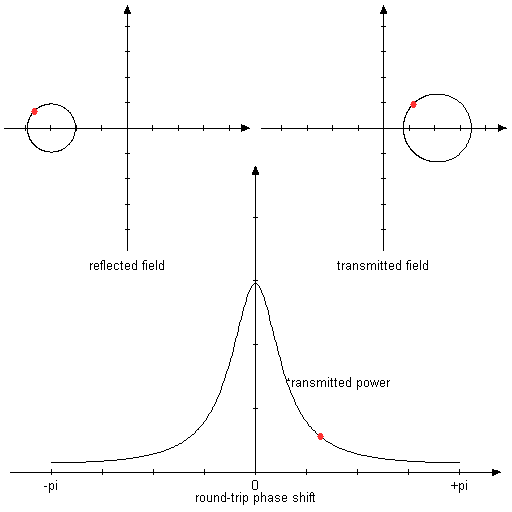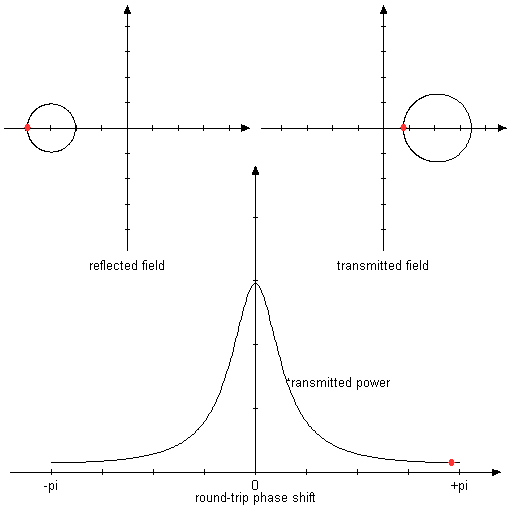
Figure 3: Same as above, but with mirror reflectivities of 80% and 50%.
In this asymmetric situation, the reflection longer goes to zero in resonance.
The analysis becomes more complicated if the incident light field has power in multiple spatial modes, since each of those may have a different round-trip phase shift related to the Gouy phase shift. This leads to different resonant frequencies for those peaks. In effect, the resonance peaks may be washed out, or (in cases with high finesse) one may even see multiple resonances in the transmission curve.
Variants
Strictly, a Fabry–Pérot interferometer by definition consists of two planar mirrors, but the term is frequently also used for resonators with curved mirrors. From a theoretical viewpoint, plane–plane optical resonators are special in the sense that their resonator modes extend up to the edges of the mirrors and experience some diffraction losses. However, Fabry–Pérot interferometers are usually used with input beams of much smaller diameter, which are actually not really matched to the resonator modes. For the usually small mirror spacings, where diffraction within a round trip is weak, this deviation is not very important.

Figure 4: Fabry–Pérot interferometer.
Normally, Fabry–Pérot interferometers are devices with free-space light propagation between the mirrors. However, the term is sometimes also used for devices containing a waveguide. For example, Fabry–Pérot lasers are laser diodes containing an active (amplifying) waveguide with some kind of mirrors at the ends.
Applications
A typical application of a Fabry–Pérot interferometer is to check whether a laser operates on a single resonator mode or on multiple modes. High-finesse Fabry–Pérot interferometers are also used as reference cavities and for spectral analysis.
For optical spectrum analysis, the Fabry–Pérot interferometer is often made short enough to achieve a sufficiently large free spectral range; the bandwidth of the resonances is then the free spectral range divided by the finesse. Due to the high reflectivities, the finesse can be high (well above 1000, and with supermirrors even much higher). For a given finesse, the wavelength resolution can be improved by increasing the mirror distance, but only at the cost of reducing the free spectral range, i.e., the range within which unique spectral assignment is possible.
A variant of the Fabry–Pérot interferometer is the Gires–Tournois interferometer. This is used not for spectral analysis, but for generating chromatic dispersion.
Frequently Asked Questions
What is a Fabry–Pérot interferometer?
A Fabry–Pérot interferometer, also called a Fabry–Pérot resonator, is a linear optical resonator consisting of two highly reflecting mirrors. It is often used as a high-resolution optical spectrometer because its transmission exhibits very sharp resonances.
How does a Fabry–Pérot interferometer work?
It operates based on interference between the multiple reflections of a light wave between its mirrors. At resonance frequencies, constructive interference leads to high transmission, while at other frequencies destructive interference causes most light to be reflected.
How can light rflection vanish at resonance?
In a symmetric, lossless interferometer at resonance, the directly reflected input field destructively interferes with the field leaking out of the resonator. This cancellation can lead to nearly zero total reflection.
How is a Fabry–Pérot interferometer used for spectral analysis?
The mirror distance can be varied, e.g., with a piezo actuator, which scans the resonance frequencies. By monitoring the transmitted power during this scan, one can measure the optical spectrum of the incident light.
Are the mirrors in a Fabry–Pérot interferometer always flat?
Strictly, the definition refers to a resonator with two planar mirrors. However, the term is also commonly used for resonators with curved mirrors, which have different properties concerning their resonator modes.
Suppliers
Sponsored content: The RP Photonics Buyer's Guide contains 14 suppliers for Fabry–Pérot interferometers. Among them:
⚙ hardware
The Fabry–Pérot interferometers offered by ALPHALAS are high-resolution spectroscopic instruments having applications in spectral analysis of narrowband light sources like gas discharge lamps and lasers. These are especially useful for analyzing the spectral content of pulsed lasers, because they allow for single-shot measurements.
The interferometers consist of two high-precision mirrors with a flatness better than λ/40 over 90% of the aperture, having broadband coatings and spacers of different thickness. The working aperture is either 22 mm or 48 mm, and the reflectivity finesse is > 120. The standard spectral range is 450 nm … 1100 nm, others on request. Combined with our CCD linear array, the interferometers form a versatile spectral analysis system.
⚙ hardware
The FPI 100 is a confocal, scanning Fabry–Pérot interferometer with a built-in photodetector unit, designed for measuring and controlling the mode profiles of continuous wave (cw) lasers. The FPI is available with different mirror sets and photodetectors for wavelength ranges between 330 nm and 3000 nm.
⚙ hardware
LightMachinery manufactures the world's finest solid and air spaced etalons. Our fluid jet polishing systems allow us to routinely create surfaces that are better than λ/100 peak to valley.
Solid etalons, air spaced etalons, piezo tunable etalons, Gires–Tournois etalons — LightMachinery has extensive expertise in the manufacturing and testing of all kinds of Fabry–Pérot etalons from 1 mm square to 100 mm in diameter. These devices require high quality, very flat optical surfaces and extreme parallelism to achieve high performance, making them a good match for the polishing and metrology at LightMachinery.
⚙ hardware
Hamamatsu Photonics offer MEMS-FPI spectroscopic modules, compact near-infrared spectrometers that incorporate a MEMS-FPI spectrum sensor and a light source.
Bibliography
| [1] | C. Fabry and A. Pérot, “Théorie et applications d’une nouvelle méthode de spectroscopie interférentielle”, Ann. de Chim. et de Phys. 16 (7), 115 (1899) |
|---|---|
| [2] | J. Stone and D. Marcuse, “Ultrahigh finesse fiber Fabry–Pérot interferometers”, J. Lightwave Technol. 4 (4), 382 (1986); doi:10.1109/JLT.1986.1074739 |
| [3] | E. D. Palik, H. Boukari and R. W. Gammon, “Experimental study of the effect of surface defects on the finesse and contrast of a Fabry–Perot interferometer”, Appl. Opt. 35 (1), 38 (1996); doi:10.1364/AO.35.000038 |
| [4] | M. Suter and P. Dietiker, “Calculation of the finesse of an ideal Fabry–Perot resonator”, Appl. Opt. 53 (30), 7004 (2014); doi:10.1364/AO.53.007004 |
| [5] | N. Ismail et al., “Fabry–Pérot resonator: spectral line shapes, generic and related Airy distributions, linewidths, finesses, and performance at low or frequency dependent reflectivity”, Opt. Express 24 (15), 16366 (2016); doi:10.1364/OE.24.016366 |
| [6] | C Saavedra et al., “Tunable fiber Fabry–Perot cavities with high passive stability”, Opt. Express 29 (2), 974 (2021); doi:10.1364/OE.412273 |
| [7] | D. Martin-Sanchez et al., “ABCD transfer matrix model of Gaussian beam propagation in Fabry–Perot etalons”, Opt. Express 30 (26), 46404 (2022); doi:10.1364/OE.477563 |
| [8] | N. Pyvovar and L. Duan, “Optical transmission of a moving Fabry–Perot interferometer”, Opt. Lett. 49 (2), 359 (2024); doi:10.1364/OL.505622 |
| [9] | A. E. Siegman, Lasers, University Science Books, Mill Valley, CA (1986) |
| [10] | J. M. Vaughan, The Fabry–Pérot Interferometer: History, Theory, Practice and Applications, CRC Press (1989) |
| [11] | R. Paschotta, Photonics Spotlight article: The resonator mystery |
(Suggest additional literature!)
Questions and Comments from Users
Here you can submit questions and comments. As far as they get accepted by the author, they will appear above this paragraph together with the author’s answer. The author will decide on acceptance based on certain criteria. Essentially, the issue must be of sufficiently broad interest.
Please do not enter personal data here. (See also our privacy declaration.) If you wish to receive personal feedback or consultancy from the author, please contact him, e.g. via e-mail.
By submitting the information, you give your consent to the potential publication of your inputs on our website according to our rules. (If you later retract your consent, we will delete those inputs.) As your inputs are first reviewed by the author, they may be published with some delay.
 optical resonators
optical resonators






