quasi-phase matching (original) (raw)
Acronym: QPM
Definition: a technique of achieving a kind of phase matching, using a periodic structure
Categories:  nonlinear optics,
nonlinear optics,  methods
methods
- optical effects
- phase matching
* critical phase matching
* noncritical phase matching
* birefringent phase matching
* quasi-phase matching
* type-I and type-II phase matching
* collinear and noncollinear phase matching
- phase matching
Related: phase matchingbirefringent phase matchingperiodic polingcoherence lengthnonlinear frequency conversionorientation-patterned semiconductors
Page views in 12 months: 3641
DOI: 10.61835/kj9 Cite the article: BibTex BibLaTex plain textHTML Link to this page! LinkedIn
Content quality and neutrality are maintained according to our editorial policy.
📦 For purchasing periodically poled nonlinear crystals, use the RP Photonics Buyer's Guide — an expert-curated directory for finding all relevant suppliers, which also offers advanced purchasing assistance.
Contents
Benefits of Quasi-phase Matching
Quasi-phase Matching of Multiple Processes
Pulse Shaping and Compression with Chirped QPM Crystals
Fabrication of Quasi-phase-matched Nonlinear Crystals
How does quasi-phase matching work?
What are the main advantages of QPM over birefringent phase matching?
Which materials are used for QPM?
Is QPM less efficient than perfect phase matching?
What are chirped QPM crystals used for?
Summary:
Quasi-phase matching (QPM) is a powerful technique in nonlinear optics for achieving efficient frequency conversion. It uses a crystal with a spatially modulated nonlinear coefficient, typically created via periodic poling, to compensate for phase mismatch between interacting waves.
A key advantage of QPM is the ability to use the largest element of a material's nonlinear susceptibility tensor and to avoid issues like spatial walk-off, often leading to significantly higher conversion efficiencies than with traditional birefringent phase matching. Common materials include periodically poled lithium niobate (PPLN), lithium tantalate (PPLT), and KTP.
The technique is widely applied in devices for frequency doubling, such as in green and blue lasers, and in optical parametric oscillators. The article also discusses advanced concepts like using chirped QPM structures for pulse shaping and compression.
(This summary was generated with AI based on the article content and has been reviewed by the article’s author.)
What is Quasi-phase Matching?
Quasi-phase matching is a technique for achieving similar results to those with phase matching of nonlinear interactions, in particular for nonlinear frequency conversion based on ($\chi^{(2)}$) nonlinearities. Instead of a homogeneous nonlinear crystal material, a material with spatially modulated nonlinear properties is used. The idea is essentially to allow for a phase mismatch over some propagation distance, but to reverse (or disrupt) the nonlinear interaction at positions where otherwise the interaction would take place with the wrong direction of conversion. In contrast to birefringent phase matching, it is not necessary to have different polarization states of the involved waves; in fact, it is most common to have equal polarization states. (The term “type-0 phase matching” is sometimes used.)

Figure 1: Addition of amplitude contributions from different parts of the crystal. With quasi-phase matching, a high conversion efficiency can be achieved.
Figure 1 illustrates with the green arrows the complex amplitude contributions from different parts of the nonlinear crystal to the harmonic wave in a frequency doubler. In the case without phase matching, these contributions cannot constructively add up over a significant distance in the crystal. With quasi-phase matching, the sign of the contributions is reversed at a point where they would otherwise diminish the total amplitude. (That is the case after propagation over one so-called coherence length.) In that way, the total amplitude can grow more and more, although not as quickly as it could for real phase matching.
Compared with the perfectly phase-matched case, QPM leads to a lower conversion efficiency if the nonlinear coefficient is the same: the effective nonlinear coefficient ($d_\textrm{eff}$) is reduced by a factor of ($2 / \pi$), and the square of that factor is relevant for the conversion efficiency. However, QPM often makes it possible to use the same polarization direction for all interacting waves, and this often corresponds to using a stronger element of the nonlinear tensor. In effect, the conversion efficiency can be substantially higher than for true phase matching. As an example, consider lithium niobate (LiNbO3), where birefringent phase matching usually utilizes the coefficient ($d_{31}$) = 4.35 pm/V, whereas QPM normally uses the higher ($d_{33}$) = 27 pm/V, which effectively results in 17 pm/V taking into account the above-mentioned factor of ($2 / \pi$). As the conversion efficiency is usually proportional to the square of the nonlinear coefficient (in the low-conversion regime), the use of _d_33 results in significant advances in cases where very high optical intensities cannot be used, e.g. due to a limited pump power. QPM is now widely used for frequency doubling (e.g. in green and blue laser sources), and for parametric devices such as optical parametric oscillators.

Figure 2: QPM for optical parametric oscillators based on periodically poled lithium niobate (PPLN) at room temperature, with all waves polarized along the z axis.
The curves correspond to poling periods between 10 μm (left-most curve) and 35 μm (right-hand side). The dotted line indicates degeneracy of signal and idler frequencies.
Benefits of Quasi-phase Matching
QPM opens many attractive possibilities. In principle, it allows for efficient nonlinear interactions with arbitrarily high “natural” phase mismatch, although a large phase mismatch may lead to impractically small poling periods. Typically, the propagation direction is along a crystal axis (noncritical phase matching), so that spatial walk-off is avoided, and the acceptance angle is large. Further, the quasi-phase matching period can be adjusted to obtain a convenient phase-matching temperature. Operation at or near room temperature is therefore often possible without resorting to critical phase matching or noncollinear phase matching. Such options are also important for nonlinear interactions in waveguides, where noncollinear beams and interactions with spatial walk-off usually cannot be used.
In short, the possible benefits of QPM are:
- It can work with a very wide range of nonlinear interactions (even in crystals which have e.g. too weak birefringence for birefringent phase matching), and this at a convenient temperature and without spatial walk-off.
- As the method of periodic poling can be applied exactly to crystal materials with particularly high nonlinearity, and QPM also often makes it possible to utilize a larger nonlinear coefficient than is accessible with birefringent phase matching, many nonlinear conversion processes can be made very efficient.
- Periodically poled crystals may have a reduced tendency for photorefractive problems, if effects in differently oriented domains cancel each other.
Limitations are:
- The fabrication of periodically poled crystals (see below) with high and reliably confirmed quality is challenging, and is possible only with certain crystal materials. The details and success rates of the required procedures depend strongly on material details – not only material type, but also defect density, stoichiometry, surface treatment and the like.
- Periodic poling can be applied only to crystals with fairly limited thickness, which excludes large aperture devices for very high power levels.
- For different processes, many different poling periods are required. This makes it less likely that a manufacturer can have the required crystal in stock. Even if the required period is in principle not problematic, a new value may require an expensive new lithographic mask. Note also that precise refractive index (Sellmeier) data are required for accurate predictions of the required poling period.
- Parasitic higher-order processes can generate light at additional wavelengths, which can be disturbing in various ways.
Quasi-phase Matching of Multiple Processes
Note that it is possible (although not common) to arrange for multiple quasi-phase-matched nonlinear interactions in a single crystal. This can be achieved e.g. by using periodically poled crystals with multiple poling periods, or by exploiting different orders of phase matching within a single poled structure. (When the duty cycle deviates from 50%, even-order processes also become possible.) Such multiple interactions can be interesting e.g. for realizing compact RGB sources.
In some cases, parasitic higher-order processes can be disturbing. For example, relatively strong green light can result from parasitic second-harmonic generation in parametric oscillators and generators made of lithium niobate or lithium tantalate which are pumped in the 1-μm spectral region. This can be detrimental particularly in the context of green-induced infrared absorption (→ photodarkening). On the other hand, weak visible parasitic beams can be helpful for the alignment of such devices.
Pulse Shaping and Compression with Chirped QPM Crystals
An extension of quasi-phase matching involves slightly non-periodic (nonuniform) poling of the nonlinear material. When the poling is done with a lithographic mask, the non-periodic poling is not more difficult to achieve than exactly periodic poling.
When a chirped QPM crystal is used for nonlinear frequency conversion, the temporal shape of the converted and/or the unconverted pulse can be modified substantially. For suitably designed chirped structures, pulses with tailored temporal shapes can be obtained.
A particular case of a non-periodic structure is a “chirped” structure, where the poling period varies monotonically along the beam direction. A possible application of such chirped QPM structures is a special method of pulse compression [4], to be used in the context of chirped-pulse amplification, for example. Here, a strongly chirped pulse is frequency-converted such that the resulting pulse is not chirped and thus much shorter. Such nonlinear compressors can handle high pulse energies, but are unfortunately fairly limited in terms of the maximum input pulse duration.
Fabrication of Quasi-phase-matched Nonlinear Crystals
The most popular technique for generating quasi-phase-matched crystals is periodic poling of ferroelectric nonlinear crystal materials such as lithium niobate (LiNbO3), lithium tantalate (LiTaO3) and potassium titanyl phosphate (KTP, KTiOPO4) by ferroelectric domain engineering. Here, a strong electric field is applied to the crystal for some time, using microstructured electrodes, so that the crystal orientation and thus the sign of the nonlinear coefficient are permanently reversed only below the electrode fingers. The poling period (the period of the electrode pattern) determines the wavelengths for which certain nonlinear processes can be quasi-phase-matched. Typical poling periods are between 5 and 50 μm. See the article on periodic poling for more details.
More recently, interesting work has been done on QPM in orientation-patterned gallium arsenide (OP-GaAs). This material has a very high nonlinear coefficient and a wide transparency range of 0.9–17 μm, making it very attractive e.g. for optical parametric oscillators emitting in the mid-infrared spectral range [6]. There are several different techniques for fabricating such materials — see the article on orientation-patterned semiconductors.
Historical Note
As a historical note, QPM was invented in 1962 [1], but could not be used at that time because suitable fabrication techniques (see below) had not then been developed. Therefore, birefringent phase matching was for a long time the only used technique. In the 1980s, however, QPM started to be used more and more extensively. The key for this was the development of advanced techniques for periodic poling.
Frequently Asked Questions
This FAQ section was generated with AI based on the article content and has been reviewed by the article’s author (RP).
What is quasi-phase matching?
Quasi-phase matching (QPM) is a technique used in nonlinear optics to achieve efficient nonlinear frequency conversion. It employs a material where the nonlinear properties are spatially modulated to compensate for the phase mismatch between the interacting light waves.
How does quasi-phase matching work?
QPM works by periodically reversing the sign of the nonlinear coefficient. This reversal occurs at positions where the energy flow would otherwise reverse direction due to phase mismatch, allowing the output power to grow continuously along the crystal.
What are the main advantages of QPM over birefringent phase matching?
QPM allows the use of a material's largest nonlinear coefficient and can be engineered for a convenient operating temperature. It also avoids spatial walk-off by allowing propagation along a crystal axis, which often results in higher conversion efficiency.
Which materials are used for QPM?
The most common method is periodic poling of ferroelectric materials like lithium niobate (LiNbO3), lithium tantalate (LiTaO3), and KTP. Orientation-patterned semiconductors like gallium arsenide (OP-GaAs) are also used, particularly for mid-infrared applications.
Is QPM less efficient than perfect phase matching?
For the same nonlinear coefficient, first-order QPM is inherently less efficient by a factor of ($ (2/\pi)^2 $). However, it often enables the use of a much larger nonlinear coefficient than is accessible with birefringent phase matching, leading to a substantial net increase in conversion efficiency.
What are chirped QPM crystals used for?
A chirped QPM crystal, where the poling period varies monotonically, can be used to modify the temporal shape of light pulses during nonlinear frequency conversion. A particular application is nonlinear pulse compression of strongly chirped pulses.
Suppliers
Sponsored content: The RP Photonics Buyer's Guide contains 13 suppliers for periodically poled nonlinear crystals. Among them:
⚙ hardware🧩 accessories and parts🧴 consumables🔧 maintenance, repair📏 metrology, calibration, testing💡 consulting🧰 development
Periodically poled lithium niobate (PPLN) crystal is a type of nonlinear optical crystal with distinguished high conversion efficiencies and a wide transparency range of 0.4–5 μm. The 5% MgO doping in LiNbO3 improves the damage threshold of the PPLN to a significant extent and broadens its phase-matching bandwidth. MgO:PPLN crystals exhibit a unique quasi-phase-matching (QPM) phenomenon, which allows the utilization of a higher nonlinear coefficient than in the case of birefringent phase matching
Shalom EO offers standard and off-the-shelf MgO:PPLN crystal and waveguides for SHG of 976 nm to 2100 nm and for various up-conversion and down-conversion applications including DFG, SFG, OPO, and OPA. Different dimensions, MgO concentrations, and AR coatings are available for selection.
⚙ hardware
MgO:PPLN non-linear optical crystals provide high efficiency wavelength conversion in the 390nm — 6000nm range. Our proprietary PPLN poling process creates high fidelity grating periods from 3.5 μm to beyond 33 μm.
We provide stock and custom free space and fiber coupled bulk crystal solutions from one-off R&D requests to high-volume OEM manufacture with customizable options including:
- free space or fiber coupled solutions
- multiple grating, chirped or fan-out designs
- tailored AR coatings
- custom grating periods and apertures
- 2×1, 2×0, 1×1 or 1×0 fiber input/output configurations
- resistive or Peltier temperature control
- integrated or external temperature control
- broad coverage from 390nm to 6000nm.
- power monitoring, control and output filtering
- compatibility with both CW and pulsed lasers
⚙ hardware
G&H's Periodically-Poled Lithium Niobate nonlinear crystals allow for efficient conversion of wavelengths in the range from visible to 5 µm. The poling pattern is lithographically defined and highly customizable allowing crystals to be used in a wide range of applications that require wavelength conversion.
Phase-matching over very long propagation lengths at infrared wavelengths is possible with our congruently grown PPLN manufactured from highly uniform Z-axis wafers.
Get in touch with us to request a quote or talk to us about a solution dedicated to your OEM application.
⚙ hardware
GWU offers periodically poled lithium niobate (PPLN) crystals with highest quality for quasi-phase matching (QPM). The sophisticated manufacturing process allows for the engineering of PPLN crystals tailored for arbitrary frequency conversion processes for full spectrum applications, covering SHG, SFG, THG, DFG, OPG, OPA and OPO. Many standard crystals are available off-the-shelf for fast shipping.
PPLN crystals can be combined with waveguide structures to enhance the conversion process, yielding high efficiency especially in weak light applications.
For maximum user convenience, our PPLN crystals are available in a robust and ready-to-use package: the PPLN Mixers. Besides being plug & play devices, the Mixers are widely customizable in wavelength and are available in free-space or fiber-coupled configurations.
⚙ hardware
HCP provides a wide selection of high-efficiency nonlinear crystals for full-spectrum applications spanning 350 to 5000 nm. Our offerings include Periodically Poled Lithium Niobate (PPLN) and Periodically Poled Lithium Tantalate (PPLT), suitable for frequency conversion processes such as SHG, SFG, DFG, OPG, OPO, OPA, and SPDC. A variety of quasi-phase matching (QPM) patterns are available—including single, multiple, fan-out, chirped, cascaded, and 2D, etc.
Key features:
- >365 kinds of commercial off-the-shelf bulk chip with oven/holder(optional) for shipping TODAY
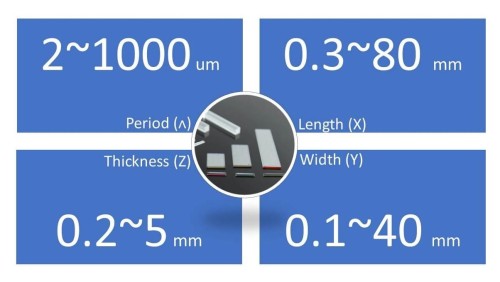
- Custom QPM designs from 2~1000 um, with chip dimensions of length (0.3~80 mm) * width (0.1~40 mm) * thickness (0.2~5 mm)
- Waveguide options with outstanding performance, including high conversion efficiency (≧65% overall efficiency), high power(8.5 W 780 nm with CW 15 W pump at 1560 nm) and wide tunability (up to 200 nm pump range)
- Fibered modules are also available for plug-and-play integration.
Bibliography
| [1] | J. A. Armstrong, “Interactions between light waves in a nonlinear dielectric”, Phys. Rev. 127 (6), 1918 (1962); doi:10.1103/PhysRev.127.1918 |
|---|---|
| [2] | L. Gordon et al., “Diffusion-bonded stacked GaAs for quasiphase-matched second-harmonic generation of a carbon dioxide laser”, Electron. Lett. 29 (22), 1942 (1993); doi:10.1049/el:19931293 |
| [3] | M. J. Angell et al., “Growth of alternating <100>/<111>-oriented II-VI regions for quasi-phase-matched nonlinear optical devices on GaAs substrates”, Appl. Phys. Lett. 64, 3107 (1994); doi:10.1063/1.111362 |
| [4] | A. Galvanauskas et al., “Chirped-pulse-amplification circuits for fiber amplifiers, based on chirped-period quasi-phase-matching gratings”, Opt. Lett. 23 (21), 1695 (1998); doi:10.1364/OL.23.001695 |
| [5] | L. A. Eyres et al., “All-epitaxial fabrication of thick, orientation-patterned GaAs films for nonlinear optical frequency conversion”, Appl. Phys. Lett. 79 (7), 904 (2001); doi:10.1063/1.1389326 |
| [6] | K. L. Vodopyanov et al., “Optical parametric oscillation in quasi-phase-matched GaAs”, Opt. Lett. 29 (16), 1912 (2004); doi:10.1364/OL.29.001912 |
| [7] | C. Zhang et al., “Perfect quasi-phase matching for the third-harmonic generation using focused Gaussian beams”, Opt. Lett. 33 (7), 720 (2008); doi:10.1364/OL.33.000720 |
| [8] | M. Charbonneau-Lefort et al., “Optical parametric amplifiers using chirped quasi-phase-matching gratings I: practical design formulas”, J. Opt. Soc. Am. B 25 (4), 463 (2008); doi:10.1364/JOSAB.25.000463 |
| [9] | M. Charbonneau-Lefort et al., “Optical parametric amplifiers using nonuniform quasi-phase-matched gratings. II: Space–time evolution of light pulses”, J. Opt. Soc. Am. B 25 (5), 680 (2008); doi:10.1364/JOSAB.25.000680 |
| [10] | A. Tehranchi and R. Kashyap, “Engineered gratings for flat broadening of second-harmonic phase-matching bandwidth in MgO-doped lithium niobate waveguides”, Opt. Express 16 (23), 18970 (2008); doi:10.1364/OE.16.018970 |
| [11] | C. R. Phillips et al., “Apodization of chirped quasi-phasematching devices”, J. Opt. Soc. Am. B 30 (6), 1551 (2013); doi:10.1364/JOSAB.30.001551 |
| [12] | N. Kovalenko, V. Hariton, K. Fritsch and O. Pronin, “Free-space quasi-phase matching”, Opt. Lett. 48 (23), 6220 (2023); doi:10.1364/OL.502825 |
(Suggest additional literature!)

Questions and Comments from Users
Here you can submit questions and comments. As far as they get accepted by the author, they will appear above this paragraph together with the author’s answer. The author will decide on acceptance based on certain criteria. Essentially, the issue must be of sufficiently broad interest.
Please do not enter personal data here. (See also our privacy declaration.) If you wish to receive personal feedback or consultancy from the author, please contact him, e.g. via e-mail.
By submitting the information, you give your consent to the potential publication of your inputs on our website according to our rules. (If you later retract your consent, we will delete those inputs.) As your inputs are first reviewed by the author, they may be published with some delay.