polarization of light (original) (raw)
Acronym: SOP = state of polarization
Definition: direction of the electric field oscillation of a light beam
Categories:  general optics,
general optics,  laser devices and laser physics
laser devices and laser physics
Related: polarization opticsunpolarized lightdepolarizerspolarization scramblerswave opticsbirefringencelasersfibersdepolarization losspolarization beam combiningpolarizersoptical activityDifferent Kinds of PolarizationConflicting Definitions of s and p Polarization
Page views in 12 months: 5537
DOI: 10.61835/pl7 Cite the article: BibTex BibLaTex plain textHTML Link to this page! LinkedIn
Content quality and neutrality are maintained according to our editorial policy.
📦 For purchasing birefringent materials, use the RP Photonics Buyer's Guide — an expert-curated directory for finding all relevant suppliers, which also offers advanced purchasing assistance.
Contents
What is Polarization of Light?
Circular and Elliptical Polarization
Radial and Azimuthal Polarization
Pure Polarization Rotation by Optical Activity
Polarization of Light in Non-isotropic Crystals
Unpolarized and Partially Polarized Beams
Relevance of Polarization for Applications
Polarization at the Photon Level
What is linear polarization of light?
What is the difference between linear and circular polarization?
What are p-polarization and s-polarization?
How can you change the polarization state of light?
What is the difference between polarized and unpolarized light?
How is polarization described mathematically?
Why do many lasers emit polarized light?
What is the connection between a photon's spin and its polarization?
Summary:
This article provides a comprehensive introduction to the polarization of light. It explains the fundamental nature of light as a transverse electromagnetic wave and details the various types of polarization, including linear, circular, elliptical, radial, and azimuthal polarization.
The text describes how optical components like waveplates and polarizers can manipulate the polarization state, and introduces the concepts of optical activity and the Faraday effect. It also covers the special cases of p and s polarization for light incident on a surface and TE/TM modes in waveguides.
Mathematical formalisms such as Jones calculus for fully polarized light and Stokes vectors for partially or unpolarized light are explained. Furthermore, the article discusses the role of polarization in non-isotropic crystals, the generation of polarized laser beams, and the quantum-mechanical description of polarization at the photon level.
(This summary was generated with AI based on the article content and has been reviewed by the article’s author.)
What is Polarization of Light?
In many respects, light can be described as a wave phenomenon (→ wave optics). More specifically, light waves are recognized as electromagnetic transverse waves, i.e., with transverse oscillations of the electric and magnetic field.
Types of Polarization
Linear Polarization
In the simplest case, a light beam is linearly polarized, which means that the electric field oscillates in a certain linear direction perpendicular to the beam axis, and the magnetic field oscillates in a direction which is perpendicular both to the propagation axis and the electric field direction. The direction of polarization is taken to be the direction of the electric field oscillations (not the magnetic ones). For example, a laser beam propagating in ($z$) direction may have the electric field oscillations in the vertical (($y$)) direction and the magnetic field oscillations in the horizontal (($x$)) direction (see Figure 1); it can be called vertically polarized or ($y$)-polarized. In a different perspective, this is also shown in the second part of Figure 2.
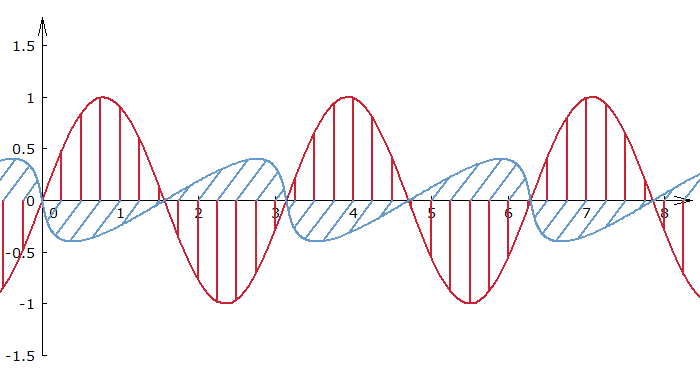
Figure 1: An electromagnetic wave traveling from left to right. The electric field (red) oscillates in the vertical direction and the magnetic field (blue) in a direction perpendicular to the drawing plane.
Of course, the polarization can have any other direction perpendicular to the beam axis. Note that a rotation of the polarization by 180° does not lead to a physically distinct state.
Circular and Elliptical Polarization
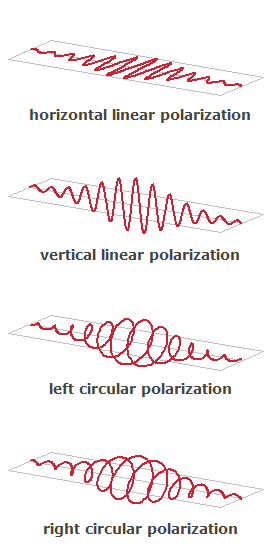
Figure 2: Different polarization states of laser emission, illustrated for a few-cycle pulse propagating from left to right.
A circular polarization state can mathematically be obtained as a superposition of electric field oscillations in the vertical and horizontal direction, both with equal strength but a relative phase change of 90°. Effectively, this leads to a rapid rotation of the electric field vector — once per optical cycle — which maintains a constant magnitude.
One distinguishes left and right circular polarization (see Figure 2). For example, left circular polarization may mean that the electric (and magnetic) field vector rotates in the left direction, seen in the direction of propagation. For an observer looking against the beam, the rotation of course has the opposite direction. Some literature defines the handedness based on that observation direction.
If the oscillations of the horizontal and vertical electric field vector do not have the same strengths, one has the case of an elliptical polarization, where the electric field vector, projected to a plane perpendicular to the propagation direction, moves along an ellipse.
Radial and Azimuthal Polarization
In the previous cases, the direction of the electric field vector was assumed to be constant over the full beam profile. However, there are light beams where that is not the case. For example, there are beams with radial polarization, where the polarization at any point on the beam profile is oriented in the radial direction, i.e., away from the beam axis.
Note that radial or azimuthal polarization state requires a zero electric field strength and thus also a vanishing optical intensity on the beam axis; it is not compatible with a Gaussian beam, for example. Radially polarized beams frequently exhibit a kind of donut profile.
A radially polarized laser beam may be generated from a linearly polarized beam with some optical element, but it is also possible to obtain radially polarized emission directly from a laser. The advantage of this approach, applied in a solid-state bulk laser, is that depolarization loss may be avoided [5]. Furthermore, there are applications benefiting from radially polarized light.
There are also azimuthally polarized beams, where the electric field direction at any point is tangential, i.e., perpendicular to a line through the point and the beam axis.
p and s Polarization
The polarization state of light often matters when light hits an optical surface under some angle. A linear polarization state is then denoted as p polarization when the polarization direction lies parallel to the plane of incidence (the plane containing the incident ray and the surface normal at the point of incidence). The polarization with a direction perpendicular to that is called s polarization. These indications have a German origin: s = senkrecht = perpendicular, p = parallel.
Unfortunately, the terms are also sometimes used with a different meaning in the context of diffraction gratings [11].
TE, TM and TEM Polarization
In the context of modes of waveguides, one often deals with TE and TM polarization:
- TE (transverse electric) means that the electric field vector is entirely transverse to the propagation direction (($E_z = 0$)). The magnetic field then usually has a non-zero component in propagation direction.
- TM (transverse magnetic) means that the magnetic field vector is entirely transverse to the propagation direction (($H_z = 0$)). The electric field then usually has a non-zero component in propagation direction.
- TEM means that both electric and magnetic field are perpendicular to the propagation direction (($E_z = 0$) and (($H_z = 0$))). Only certain waveguides (multi-conductor waveguides like coax or parallel-plate) support true TEM modes. Fibers do not support TEM modes.
Most optical fibers are weakly guiding, which implies that longitudinal field components are weak, thus often neglected; electric and magnetic fields are nearly perpendicular to the propagation axis. One commonly deals with a scalar model, having simpler LP modes. (LP means “linearly polarized”, which is not particularly clear, since TE and TM modes are also linearly polarized, and in scalar models polarization is not part of mode calculations.) For a more accurate analysis, one can consider vector modes HE, EH, TE and TM, where HE and EH are hybrid modes, having non-zero electric and magnetic longitudinal components. LP modes correspond to nearly degenerate groups of vector modes.
It is less common in optics to use TE and TM for incidence of a beam on an optical surface, but in that case one can identify TE polarization with s polarization, and TM is p polarization. Here, one considers the plane of incidence rather than longitudinal field components.
Effects of Optical Components
Waveplates
The polarization state of light is often manipulated using different kinds of optical waveplates. Some examples:
- With a half waveplate (($\lambda$)/2 plate), one may rotate a linear polarization state into any other direction.
- With a quarter waveplate (($\lambda$)/4 plate), having its axis oriented at 45° to the polarization direction, one may convert a linear polarization state to a circular one (and vice versa).
- With a combination of one half waveplate and two quarter waveplates, one can realize a polarization controller, with which one can do arbitrary polarization conversions by properly rotating the three plates.
Pure Polarization Rotation by Optical Activity
As explained above, a waveplate or other birefringent optical element may rotate the direction of linear polarization, but more generally one will obtain an elliptical polarization state after such an element. Pure polarization rotation, where a linear polarization state is always maintained (just with variable direction), can occur in the form of optical activity. Some optically active substances such as ordinary sugar (saccharose) can produce rotation angles of several degrees already within e.g. a few millimeters of propagation length. Optical activity can be accurately measured with polarimeters.
Optical activity arises in chiral media; the observed rotation in such a solution is proportional to path length and the enantiomeric excess (concentration difference).
Optical activity can also be induced by a magnetic field in a substance which is not naturally optically active. That is called the Faraday effect, and is exploited in Faraday rotators and Faraday isolators.
Polarization of Light in Non-isotropic Crystals
When light propagates in a non-isotropic medium, such as a nonlinear crystal, the direction of polarization relative to the crystal axes is relevant. This is not the direction of beam propagation, but rather perpendicular to that.
In simple cases, one has a polarization direction along one of the axes of the crystal lattice. One may then call this c polarization, for example, if it is along the crystal's c axis. (Unfortunately, for one type of crystal, there are sometimes different ways of labeling the crystal axes.)
Frequently, however, one requires a propagation direction which is not aligned with one of the crystal axes — for example, in the context of critical phase matching. The article on critical phase matching contains an example case for type I phase matching of frequency doubling in LBO, where the pump and second-harmonic beams propagate within the XY plane with an angle ($\varphi$) against the X axis). In this situation, polarization can be either ordinary or extraordinary:
- Ordinary means in that case polarization in the Z direction — independent of the angle ($\varphi$).
- Extraordinary means that the electric field vector is in the XY plane with the angle ($\varphi$) against the Y (not X) axis, perpendicular to the beam direction.
For the mentioned phase-matching scheme, which is denoted as XY oo-e, the pump wave has ordinary polarization, while the second-harmonic wave has extraordinary polarization. There are also cases with type II phase matching, e.g. the scheme XY oe-e, where the pump wave has both an ordinary and an extraordinary polarization component.
Jones Calculus
The polarization state of monochromatic light is often described with a Jones vector, having complex electric field amplitudes for ($x$) and ($y$) direction, if propagation occurs in ($z$) direction. That Jones vector may be constant over some area across the beam, or it may vary, for example for a radially polarized beam (see above). The effect of optical elements such as waveplates, polarizers and Faraday rotators can be described with Jones matrices, with which the Jones vectors can be transformed by multiplication. (One assumes a linear relationship between input and output amplitudes.) A whole sequence of such optical elements can be described with a single Jones matrix, which is obtained as the product of the matrices corresponding to the components.
There are cases where polychromatic light can be described with a single Jones vector, since all its frequency components have essentially the same polarization state. However, the polarization state is substantially frequency-dependent in other cases.
Jones vectors can be used only for fully defined polarization states, not for unpolarized or partially polarized beams (see below) having a stochastic nature.
Unpolarized and Partially Polarized Beams
As a somewhat simplified way, a light beam is often called unpolarized when the analysis with a linear polarizer results in 50% of the power to be transmitted, regardless of the rotational orientation. (See the article on unpolarized light for more details.) Microscopically, this usually means that the polarization state is randomly fluctuating over time, so that on average no polarization is detected. Note that such fluctuations are not possible for strictly monochromatic light.
Linearly polarized light can be depolarized (made unpolarized) with a polarization scrambler, which applies the mentioned random polarization changes, or at least quasi-random changes. Static (not time-dependent) pseudo-depolarization can be achieved with various types of depolarizers.
There are also partially polarized states of light. These can be described with Stokes vectors (but not with Jones vectors). Further, one can define a degree of polarization which can be calculated from the Stokes vector and can vary between 0 (unpolarized) and 1 (fully polarized).
Fully polarized states can be associated with points on the so-called Poincaré sphere. Partially polarized states correspond to points inside that sphere; unpolarized light is represented by the point at its center.
Polarization Extinction Ratio
The degree of linear polarization is often quantified with the polarization extinction ratio (PER), defined as the ratio of optical powers in the two polarization directions. It is measured by recording the orientation-dependent power transmission of a polarizer, and often specified in decibels: \textrm{PER}_\textrm{dB} = 10 \: | \lg \frac{P_{∥}}{P_{⟂}} |$$
Of course, for accurate measurements the extinction ratio of the polarizer itself must be higher than that of the laser beam.
Relevance of Polarization for Applications
The polarization of light is important for a range of applications. Some examples are:
- setups where minimum reflection losses are obtained only for p polarization at optical surfaces (→ Brewster's angle)
- nonlinear frequency conversion, where phase matching in a nonlinear crystal is normally obtained only for one polarization direction
- processing of laser beams in polarization-dependent devices, such as interferometers, systems with polarization beam combining, semiconductor optical amplifiers, and optical modulators
Polarization of Laser Beams
In many cases, the output of a laser is a linearly polarized laser beam. Different mechanisms can be responsible for that:
- The laser gain may be polarization dependent. This is the case in some anisotropic laser crystals (e.g. Nd:YVO4 or Nd:YLF), but also in some semiconductor optical amplifiers. Even in isotropic materials, the gain may become somewhat polarization-dependent by polarized optical pumping.
- The resonator losses may be polarization-dependent, e.g. when the resonator contains a Brewster plate or even only a slightly tilted optical component.
Note that a very small gain or loss difference for the two polarization directions can be sufficient for obtaining a stable linear polarization, provided that there is no significant coupling of polarization modes within the laser resonator.
On the other hand, the polarization state of the laser output can be disturbed e.g. by random (and temperature-dependent) birefringence, such as occurs e.g. in optical fibers (if they are not polarization-maintaining or single-polarization fibers) and also in laser crystals or glasses as a result of thermal effects (→ depolarization loss). If the laser gain is not polarization-dependent, small drifts of the birefringence may lead to large changes in the polarization state, and also a significant variation in the polarization state across the beam profile.
Polarization at the Photon Level
At the photon level, polarization of light is related to the quantum state associated with the direction of the photon's electric field oscillation. This is a direct quantum analogue of classical polarization, describing how the electromagnetic field vector (specifically, the electric field) varies as the photon propagates.
A single photon can exist in a state of linear polarization (e.g., horizontal or vertical), circular polarization (right or left-handed), or any quantum superposition of these basis states.
The photon’s polarization state is mathematically described using a two-dimensional Hilbert space — analogous to the Jones vector formalism used in classical optics. Any polarization state can be written as a superposition of two orthogonal linear polarizations (e.g., ($∣x\rangle$) and ($∣y\rangle$)) or the two orthogonal circular polarizations.
The spin angular momentum of a photon is directly connected to its polarization. For a photon propagating along the z axis:
- right-circular polarization (($σ+$)): spin angular momentum = +ℏ (helicity +1)
- left-circular polarization (($σ–$)): spin angular momentum = –ℏ (helicity –1)
(The opposite convention also appears in the literature, e.g. ($σ+ ↔ –ℏ$).)
For photons, spin (more precisely, helicity) is always aligned or anti-aligned with their momentum. A spin measurement will always force a photon into a left- or right-circular polarization state, while a linear polarization measurement will force it into a linear polarization state.
Frequently Asked Questions
This FAQ section was generated with AI based on the article content and has been reviewed by the article’s author (RP).
What is linear polarization of light?
A light beam is linearly polarized when its electric field oscillates back and forth along a single, fixed line that is perpendicular to the direction of propagation. This line defines the direction of polarization.
What is the difference between linear and circular polarization?
In linearly polarized light, the electric field vector oscillates along a fixed line. In circularly polarized light, the electric field vector rotates in a circle around the propagation axis while maintaining a constant magnitude, which results from two perpendicular linear components having equal amplitude and a 90° phase difference.
What are p-polarization and s-polarization?
When light strikes a surface, p- and s-polarization describe its linear polarization relative to the plane of incidence. P-polarization is parallel to this plane, while s-polarization is perpendicular (from the German 'senkrecht') to it.
How can you change the polarization state of light?
The polarization of light is commonly manipulated using optical components called waveplates. A half-waveplate can rotate the direction of linear polarization, and a quarter-waveplate can convert linear to circular polarization and vice versa.
What is the difference between polarized and unpolarized light?
Polarized light has a well-defined orientation of its electric field oscillations, such as linear or circular. In contrast, unpolarized light consists of a random and rapidly fluctuating mix of polarization states, so no specific polarization is observed on average.
How is polarization described mathematically?
The state of fully polarized monochromatic light is described by a Jones vector, representing the complex electric field amplitudes. For partially polarized or unpolarized light, Stokes vectors and the Poincaré sphere are used to provide a complete description.
Why do many lasers emit polarized light?
Many lasers emit linearly polarized light because either the laser gain is polarization-dependent (anisotropic) or the laser resonator contains elements like a Brewster plate that cause higher losses for one polarization, allowing the other to dominate.
What is the connection between a photon's spin and its polarization?
A photon's spin angular momentum is directly related to its circular polarization. A right-circularly polarized photon has a spin of +ℏ aligned with its motion, while a left-circularly polarized photon has a spin of –ℏ.
Suppliers
Sponsored content: The RP Photonics Buyer's Guide contains 26 suppliers for birefringent materials. Among them:
⚙ hardware
We offer a wide range of polarizers and polarization optics for many different uses. Choosing the right polarization optic for your application can be a bewildering task, as we offer a wide range for many different uses.
A brief tutorial is available on our website.
Feel free to contact us for assistance. Our experienced staff is only too pleased to help you with the decision process.
⚙ hardware🧩 accessories and parts🧴 consumables🔧 maintenance, repair📏 metrology, calibration, testing💡 consulting🧰 development
Shalom EO offers various birefringent materials, including: MgF2 crystals, LiNbO3 and alpha-BBO crystals, quartz crystals, calcite crystals, and YVO4 crystals. The crystals exhibit excellent properties when used to make waveplates, Glan and Thompson polarizers, and other optical components. Crystal ingots, blanks, and polished and coated optical elements made of birefringent crystals are offered according to your request.
Shalom EO also offers other optical crystal materials, including: nonlinear crystals, laser crystals, and electric-optical and acousto-optic crystals.
Bibliography
| [1] | V. G. Niziev and A. V. Nesterov, “Influence of beam polarization on laser cutting efficiency”, J. Phys. D 32 (13), 1455 (1999); doi:10.1088/0022-3727/32/13/304 |
|---|---|
| [2] | A. V. Nesterov and V. G. Niziev, “Laser beams with axially symmetric polarization”, J. Phys. D 33 (15), 1817 (2000); doi:10.1088/0022-3727/33/15/310 |
| [3] | Q. Zhan and J. Leger, “Focus shaping using cylindrical vector beams”, Opt. Express 10 (7), 324 (2002); doi:10.1364/OE.10.000324 |
| [4] | P. J. Leo, G. R. Gray, G. J. Simer and K. B. Rochford, “State of polarization changes: classification and measurement”, J. Lightwave Technol. 21 (10), 2189 (2003) |
| [5] | I. Moshe et al., “Production of radially or azimuthally polarized beams in solid-state lasers and the elimination of thermally induced birefringence effects”, Opt. Lett. 28 (10), 807 (2003); doi:10.1364/OL.28.000807 |
| [6] | ISO Standard 12005, “Lasers and laser-related equipment — Test methods for laser beam parameters — Polarization” |
| [7] | Q. Zhan, “Cylindrical vector beams: from mathematical concepts to applications”, Advances in Optics and Photonics 1 (1), 1 (2009); doi:10.1364/AOP.1.000001 |
| [8] | M. Rumpel et al., “Circular grating waveguide structures for intracavity generation of azimuthal polarization in a thin-disk laser”, Opt. Lett. 37 (10), 1763 (2012); doi:10.1364/OL.37.001763 |
| [9] | A. Z. Goldberg et al., “Quantum concepts in optical polarization”, Advances in Optics and Photonics 13 (1), 1 (2021); doi:10.1364/AOP.404175 |
| [10] | M. A. Alonso, “Geometric descriptions for the polarization of nonparaxial light: a tutorial”, Advances in Optics and Photonics 15 (1), 176 (2023); doi:10.1364/AOP.475491 |
| [11] | R. Paschotta, “Conflicting definitions of s and p polarization”, The Photonics Spotlight 2012-03-03 |
(Suggest additional literature!)
Questions and Comments from Users
Here you can submit questions and comments. As far as they get accepted by the author, they will appear above this paragraph together with the author’s answer. The author will decide on acceptance based on certain criteria. Essentially, the issue must be of sufficiently broad interest.
Please do not enter personal data here. (See also our privacy declaration.) If you wish to receive personal feedback or consultancy from the author, please contact him, e.g. via e-mail.
By submitting the information, you give your consent to the potential publication of your inputs on our website according to our rules. (If you later retract your consent, we will delete those inputs.) As your inputs are first reviewed by the author, they may be published with some delay.



