birefringence (original) (raw)
Definition: the polarization dependence of the refractive index of a medium
optical properties of materials
- absorptance
- absorption coefficient
- absorption length
- birefringence
- chromatic dispersion
- dichroism
- emissivity
- group delay dispersion
- group index
- group velocity
- nonlinear index
- opacity
- optical activity
- optical density
- polarization beat length
- principal dispersion
- propagation losses
- refractive index
- Sellmeier formula
- thermo-optic effect
- transparency
- (more topics)
-
- absorption
- birefringence
- diffraction
- dispersion
- dispersive waves
- evanescent waves
- Faraday effect
- focusing
- imaging
- interference
- optical aberrations
- optical phase shifts
- phase matching
- photodarkening
- polarization changes
- propagation losses
- reflection
- refraction
- scattering
- spatial walk-off
- superluminal transmission
- temporal walk-off
- thermal blooming
- thermal radiation
- total internal reflection
- wavefront distortions
- nonlinear optical effects
- electro-optic effect
- (more topics)
Related: retardancerefractionpolarization of lightpolarization beat lengthbirefringent tunersbirefringent phase matchingpolarization-maintaining fibersspatial walk-offfiber polarization controllersLyot filtersFaraday effectOptical Isotropy: Nonlinear Interactions are Different!
Page views in 12 months: 7797
DOI: 10.61835/v8r Cite the article: BibTex BibLaTex plain textHTML Link to this page! LinkedIn
Content quality and neutrality are maintained according to our editorial policy.
📦 For purchasing birefringent materials, use the RP Photonics Buyer's Guide — an expert-curated directory for finding all relevant suppliers, which also offers advanced purchasing assistance.
Contents
Definition of Birefringence
Birefringence is the property of some transparent optical materials that the refractive index depends on the polarization direction — which is defined as the direction of the electric field. For example, it is observed for crystalline quartz, calcite, sapphire and ruby. It is also found in various laser crystal materials such as Nd:YVO4, Nd:YLF and Nd:YAlO3, and in nonlinear crystal materials like LiNbO3, LBO and KTP. Figure 1 shows the birefringence of α-quartz.
The term birefringence is sometimes also used as a quantity (see below), usually defined as the difference between extraordinary and ordinary refractive index at a certain optical wavelength.
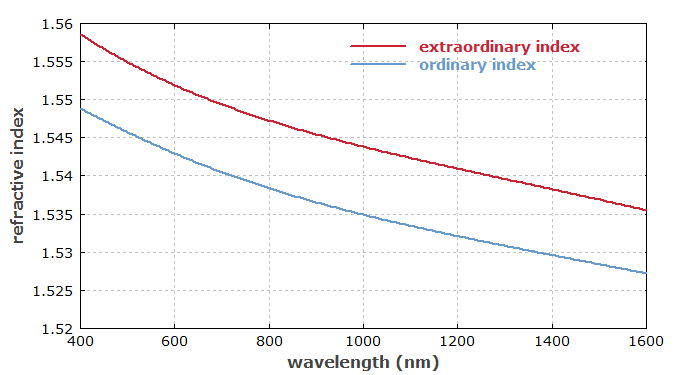
Figure 1: Refractive indices of α-quartz vs. wavelength. For this positive uniaxial material, the extraordinary index is higher.
Intrinsic and Induced Birefringence
Birefringence can occur only in optically non-isotropic materials. Often, it results from non-cubic lattice structures of optical crystals, i.e., an intrinsic anisotropy.
In other cases, birefringence can be induced in originally isotropic optical materials (e.g. crystals with cubic structure, glasses or polymers); these can become anisotropic due to the application of some external influence which breaks the symmetry:
- In some cases, mechanical stress has that effect. That can easily be observed with a piece of acrylic between two crossed polarizers: when stress is applied to the acrylic, one observes colored patterns resulting from the wavelength-dependent effect of stress-induced birefringence.
- In other cases, application of a strong electric field has similar effects, e.g. in glasses. The temporary application of such a field can even cause a frozen-in polarization, which means that the induced birefringence remains even after removing the external field.
In optical fibers, birefringence can be caused by an elliptical shape of the fiber core, by other asymmetries of the fiber design (particularly for photonic crystal fibers), or by mechanical stress (e.g. caused by bending). In the case of polymers (plastics), birefringence can result from the ordering of molecules which is caused by an extrusion process, for example.
Uniaxial and Biaxial Optical Materials
Depending on the symmetry of the crystal structure, a crystalline optical material can be uniaxial or biaxial.
Uniaxial Crystals
The simpler case is that of uniaxial crystals (examples: calcite, quartz, sapphire, LiNbO3, β-BaB2O4 = BBO). Those have a so-called optical axis, and the refractive index for given wavelength depends on the relative orientation of electric field director and optical axis:
- If the electric field has the direction of the optical axis, one obtains the extraordinary index ($n_\textrm{e}$). This is possible only if the propagation direction (more precisely, the direction of the ($k$) vector) is perpendicular to the optical axis. For the other polarization direction, one then obtains the ordinary index ($n_\textrm{o}$).
- For propagation along the optical axis, the electric field can only be perpendicular to that axis, so that one obtains the ordinary index for any polarization direction. In that situation, no birefringence is experienced.
- For an arbitrary angle ($\theta$) between propagation direction and optical axis, one can find two linear polarization directions exhibiting different refractive indices. The first one is perpendicular to the ($k$) vector and the optical axis; here, we have the ordinary index ($n_\textrm{o}$), and such a wave is called an ordinary wave. The other polarization direction is perpendicular to that and to the ($k$) vector. The latter has a refractive index which is generally not the extraordinary index ($n_\textrm{e}$), but rather a mixture of ($n_\textrm{e}$) and ($n_\textrm{o}$). This can be calculated with the following equation: n = \frac{1}{{\sqrt {\frac{{{{\cos }^2}\theta }}{{n_{\rm{o}}^2}} + \frac{{{{\sin }^2}\theta }}{{n_{\rm{e}}^2}}} }}$$
The equation shows that for ($\theta \rightarrow 0$) (i.e., propagation along the optical axis) we obtain ($n \rightarrow n_\textrm{o}$), and the observed birefringence vanishes: one obtains ($n_\textrm{o}$) for any polarization direction.
One distinguishes positive and negative uniaxial crystals; in the former case, the extraordinary index is higher than the ordinary index.
Biaxial Crystals
For biaxial crystals (examples: mica, CaTiO3 = perovskite, LiB3O5 = LBO), such calculations are substantially more complicated, at least for arbitrary propagation directions. There are three mutually orthogonal principal axes associated with different refractive indices. Frequently, however, one deals with cases where the propagation direction is in one of the planes spanned by the principal axes of index ellipsoid, and in such cases the calculation is again reasonably simple. This is usually the case in calculations for phase matching of nonlinear frequency conversion processes.
For optical fibers and other waveguides, the distinction between uniaxial and biaxial does not apply, since the propagation direction is essentially determined by the waveguide.
Consequences of a Polarization-dependent Refractive Index
The polarization dependence of the refractive index can have a variety of effects, some of which are highly important in nonlinear optics and laser technology:
Double Refraction
When a beam is refracted at the surface of a birefringent crystal, the refraction angle depends on the polarization direction. An unpolarized light beam can then be split into two linearly polarized beams when hitting surfaces of the material with non-normal incidence (double refraction). When some object, which is illuminated with unpolarized light, is viewed through a birefringent crystal (e.g. made of calcite), two images occur which are slightly displaced.
Changes in Polarization States
If a linearly polarized laser beam propagates through a birefringent medium, there are generally two polarization components with different wavenumbers. Therefore, the optical phases of the two linear polarization components evolve differently, and consequently the resulting polarization state (from the superposition of the two components) changes during propagation. This effect can be applied, for example, in birefringent tuners because it is wavelength-dependent (even if the difference in refractive indices is not wavelength-dependent). It can also be power-dependent (→ nonlinear polarization rotation) through self- and cross-phase modulation, e.g. in an optical fiber, and this effect is sometimes used for passive mode locking of fiber lasers.
Similarly, the polarization state of a laser beam in a laser crystal with thermally induced birefringence is distorted. The kind of distortion depends on the position, since the birefringent axis has a varying (e.g. always radial) orientation. This effect (combined with a polarizing optical element in the laser resonator) is the origin of depolarization loss.
Birefringent Phase Matching
The birefringence of nonlinear crystal materials allows for birefringent phase matching of nonlinear interactions. Essentially, this means that birefringence compensates the wavelength dependence of the refractive index. This is the most common method of phase matching for various types of nonlinear frequency conversion such as frequency doubling and optical parametric oscillation.
Spatial Walk-off
For extraordinary waves, where the refractive index depends on the angular orientation, there is a spatial walk-off: the direction of power propagation is slightly tilted against that of the ($k$) vector. This effect can severely limit the efficiency of nonlinear frequency conversion processes, particularly when using tightly focused laser beams.
Temporal Walk-off Due to Group Velocity Mismatch
Not only the refractive index, but also the group index becomes polarization-dependent. This matters e.g. for the propagation of ultrashort pulses: Components with different polarization propagate with different group velocities. If a femtosecond pulse propagates through a piece of birefringent material, the polarization components experience different group delays (time delays); the pulse may effectively be split into two pulses. That group velocity mismatch can be exploited in divided-pulse amplification, for example.
For a numerical example, we again consider α-quartz and assume a wavelength of 1060 nm. The group indices for ordinary and extraordinary polarization, respectively, are 1.549353 and 1.558489. Within a crystal length of ($L$) = 10 mm, this causes a differential time delay of ($L (n_g - n_o) / c$) = 305 fs.
Examples of Applications of Birefringence in Photonics
In laser technology and nonlinear optics, the phenomenon of birefringence occurs mainly in the context of non-isotropic crystals:
- Birefringent crystals are also used for making optical components of various types, for example polarizers, waveplates, Lyot filters, Berek compensators, different types of depolarizers and group velocity delay compensation plates.
- Some laser crystals (e.g. vanadate, YLF and tungstate crystals) are naturally birefringent. This is often helpful for obtaining a linearly polarized output without depolarization loss.
- All nonlinear crystals for nonlinear frequency conversion are birefringent. This is because they can have their ($\chi^{(2)}$) nonlinearity only by being non-isotropic, and that also causes birefringence. In many cases, the birefringence is utilized for birefringent phase matching.
- Straight optical fibers are often nominally symmetric, but nevertheless exhibit some small degree of random birefringence because of tiny deviations from perfect symmetry — for example due to bending, other mechanical stress or small microscopic irregularities. There are polarization-maintaining fibers, which have an intentionally introduced stronger birefringence.
Quantifying Birefringence
The magnitude of birefringence can be specified in different ways:
- For an optical component with some birefringence, one can specify the retardance, which is the difference in phase shifts for the two polarization directions.
- For bulk optical materials, it is also common to consider the difference of refractive indices for the two polarization directions. The larger that difference, the larger the obtained retardance per millimeter of propagation length.
- For optical fibers and other waveguides, it is more appropriate to consider the difference of effective refractive indices. This is directly related to the difference in the propagation constants (phase constants).
- Alternatively, one may specify the polarization beat length, which is ($2\pi$) divided by the difference of the propagation constants. If waves with different polarization directions propagate together in the waveguide, their phase relation is restored after integer multiples of the propagation beat length.
Circular Birefringence
Beyond the ordinary kind of (linear) birefringence, there is also the phenomenon of circular birefringence. Here, the refractive index differs between left-hand and right-hand circular polarization. Circular birefringence can be induced by a magnetic field; this is called the Faraday effect. See the article on optical activity for details.
Frequently Asked Questions
What is birefringence?
Birefringence is the property of an optical material where its refractive index depends on the polarization direction of light. As a result, light rays with different polarizations propagate at different speeds.
What causes birefringence in materials?
Birefringence can be an intrinsic property of crystals with an anisotropic (non-cubic) lattice structure. It can also be induced in isotropic materials like glass by external factors such as mechanical stress or a strong electric field.
What is the difference between uniaxial and biaxial crystals?
Uniaxial crystals have a single 'optical axis', and the refractive index depends on the angle relative to this axis. Biaxial crystals are more complex, with three distinct principal axes, each associated with a different refractive index.
What is double refraction?
Double refraction is an effect of birefringence where an unpolarized light beam entering a birefringent crystal at an angle is split into two separate beams with orthogonal linear polarizations.
How is birefringence used in nonlinear optics?
Birefringence is essential for phase matching in nonlinear frequency conversion. It allows the different refractive indices seen by orthogonally polarized waves to compensate for chromatic dispersion, which is crucial for efficient processes like frequency doubling.
Can an optical fiber exhibit birefringence?
Yes. While standard fibers have low random birefringence, polarization-maintaining fibers are specifically designed with high birefringence, created by an elliptical core or built-in stress, to preserve the polarization state of light traveling through them.
Suppliers
Sponsored content: The RP Photonics Buyer's Guide contains 26 suppliers for birefringent materials. Among them:
⚙ hardware
We offer a wide range of polarizers and polarization optics for many different uses. Choosing the right polarization optic for your application can be a bewildering task, as we offer a wide range for many different uses.
A brief tutorial is available on our website.
Feel free to contact us for assistance. Our experienced staff is only too pleased to help you with the decision process.
⚙ hardware🧩 accessories and parts🧴 consumables🔧 maintenance, repair📏 metrology, calibration, testing💡 consulting🧰 development
Shalom EO offers various birefringent materials, including: MgF2 crystals, LiNbO3 and alpha-BBO crystals, quartz crystals, calcite crystals, and YVO4 crystals. The crystals exhibit excellent properties when used to make waveplates, Glan and Thompson polarizers, and other optical components. Crystal ingots, blanks, and polished and coated optical elements made of birefringent crystals are offered according to your request.
Shalom EO also offers other optical crystal materials, including: nonlinear crystals, laser crystals, and electric-optical and acousto-optic crystals.
Bibliography
| [1] | R. Ulrich et al., “Bending-induced birefringence in single-mode fibers”, Opt. Lett. 5 (6), 273 (1980); doi:10.1364/OL.5.000273 |
|---|---|
| [2] | S. J. Garth, “Birefringence in bent single-mode fibers”, IEEE J. Lightwave Technol. 6 (3), 445 (1988); doi:10.1109/50.4022 |
| [3] | J. Pabón, K. Salazar and R. Torres, “Characterization method of the effective phase retardation in linear birefringent thin sheets”, Appl. Opt. 60 (14), 4251 (2021); doi:10.1364/AO.422820 |
(Suggest additional literature!)
Questions and Comments from Users
Here you can submit questions and comments. As far as they get accepted by the author, they will appear above this paragraph together with the author’s answer. The author will decide on acceptance based on certain criteria. Essentially, the issue must be of sufficiently broad interest.
Please do not enter personal data here. (See also our privacy declaration.) If you wish to receive personal feedback or consultancy from the author, please contact him, e.g. via e-mail.
By submitting the information, you give your consent to the potential publication of your inputs on our website according to our rules. (If you later retract your consent, we will delete those inputs.) As your inputs are first reviewed by the author, they may be published with some delay.
 general optics
general optics


