Thermodynamics and Mechanics of Membrane Curvature Generation and Sensing by Proteins and Lipids (original) (raw)

. Author manuscript; available in PMC: 2014 Oct 21.

Abstract

Research investigating lipid membrane curvature generation and sensing is a rapidly developing frontier in membrane physical chemistry and biophysics. The fast recent progress is based on the discovery of a plethora of proteins involved in coupling membrane shape to cellular membrane function, the design of new quantitative experimental techniques to study aspects of membrane curvature, and the development of analytical theories and simulation techniques that allow a mechanistic interpretation of quantitative measurements. The present review first provides an overview of important classes of membrane proteins for which function is coupled to membrane curvature. We then survey several mechanisms that are assumed to underlie membrane curvature sensing and generation. Finally, we discuss relatively simple thermodynamic/mechanical models that allow quantitative interpretation of experimental observations.

Keywords: curvature-composition coupling, giant unilamellar vesicle, lipid membrane, tube

INTRODUCTION

Historically, membrane curvature (MC) was considered a passive geometric feature of biological membranes. More recently, the concept that MC provides an active means to control the spatial organization and activity of cells has emerged (1, 2). Consequently, there is a growing recognition of the importance of the abundance of peripheral membrane proteins that contribute to MC sensing and generation (MC-S&G). The malfunction of many of these proteins is implicated in disease (3), motivating their investigation as a frontier of membrane biophysics. Two particularly active areas have been (a) in vitro structural characterization, employing techniques such as X-ray crystallography and electron microscopy (EM) (4–28), nuclear magnetic resonance (22, 29–31), and electron spin resonance spectroscopies (14, 17, 27, 32, 33), and (b) cell biological studies based on fluorescence imaging of labeled proteins (10, 12, 16, 19, 20, 24, 33, 34). More recently, model membrane fluorescence imaging (35–37) in combination with mechanical membrane manipulation (38–46) has provided novel quantitative characterization of MC-S&G principles and unprecedented connection to thermodynamic and mechanical membrane theory.

Several recent reviews have summarized the field of MC-S&G by lipids and proteins (1–3, 47–58). The purpose of the present contribution is to provide an overview of the major families of proteins that are believed to be involved in MC-S&G, then to survey several of the currently debated mechanisms for these phenomena, and finally to review relatively straightforward thermodynamic and mechanical models that have been used to interpret experimental observations of lipid and protein sorting and MC generation. We conclude by suggesting interesting key aspects to be addressed in the near future.

MAJOR CLASSES OF CURVATURE-GENERATING AND -SENSING PROTEINS

We consider three major classes of proteins involved in MC-S&G, roughly defined by structural features. The first of these classes is represented by BAR domain family proteins (Bin/Amphiphysin/Rvs). BAR domains are crescent-shaped dimeric α-helical bundles that in many cases bind to membranes through both electrostatic and hydrophobic interactions. Several different types of BAR domains can be distinguished based on structural characteristics, including classical BAR, N-BAR, F-BAR, I-BAR, and PX-BAR (for details, see 3, 51, 59). The second class is represented by dynamin family proteins (including Eps15 homology domain–containing proteins); these proteins do not contain BAR domains (60, 61). Proteins of these two families show structural features believed to generate MC via scaffolding (see below for a discussion of this mechanism).

The third class considered here includes proteins and protein domains not expected to exhibit scaffolding on the basis of structure. Rather, proteins belonging to the third class bear structural units that can lead to MC-S&G by inserting (wedging) into the membrane. Commonly, the inserting regions are intrinsically unfolded appendices that undergo folding transitions to form amphipathic α-helices (AHs) upon membrane binding. Members of this class include epsin N-terminal homology (ENTH) domain-containing proteins such as epsin, which is believed to be involved in clathrin-mediated endocytosis (8). Additional members are Arf1 (28, 62, 63) and Sar1 (13), small GTPases involved in coatomer complex formation (COPI and COPII, respectively), in which MC initiated by wedging could be amplified and stabilized by additional scaffold components of the coatomer complexes (64, 65). The membrane-inserting, helix-forming ALPS (ArfGAP1 or amphipathic lipid-packing sensor) motif is an element common to curvature sensors ArfGAP1 (41, 66–68), the golgin GMAP-210 (69), and additional proteins that show curvature-dependent vesicle binding (70). Membrane-dependent helix formation associated with MC-S&G is not limited to local regions of proteins, as the entirely intrinsically unfolded Parkinson’s disease–related protein α-synuclein (22, 71) also exhibits this property and therefore belongs in the third class of MC-S&G proteins.

Some recently identified proteins and protein complexes involved in MC-S&G may belong to one of the classes defined above but cannot yet be classified as their structures have not been sufficiently characterized. Proteins of the reticulon family, in combination with the DP1/Yop1p family, are assumed to contribute to the generation of the curvature of tubular endoplasmic reticulum membranes (19, 54). Additional proteins believed to function as MC promoters include caveolins and cavins (54, 55, 72) of caveolae (flask-shaped plasma membrane invaginations).

Further examples of protein coats involved in MC-S&G include retromer and ESCRT (endosomal sorting complex required for transport). Retromer is a peripheral membrane protein assembly consisting of a cargo-loading subcomplex and an additional complex involving sorting nexins with BAR domains (10, 73). The ESCRT consists of four complexes that function to achieve cargo sorting, membrane invagination, and fission to generate intralumenal vesicles of the late endosomal compartment (74–76).

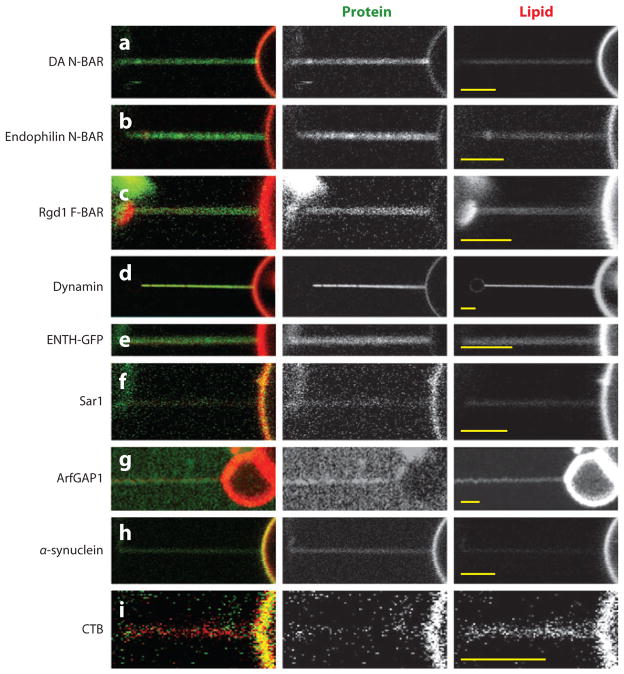
We note that for many of the above mentioned proteins and protein domains, curvature generation has been demonstrated by means of vesicle tubulation revealed by EM imaging. For thermodynamic reasons (see below), the ability of a protein to generate curvature necessarily implies a tendency of the protein to also sense MC. Indeed, members of all three protein classes defined above have been observed to sense MC. Figures 1a–h demonstrate MC sensing by the observation of preferential partitioning of fluorescently tagged proteins onto highly curved tubular membranes.

Figure 1.

Figure 1

Confocal micrographs demonstrating protein curvature partitioning among tubular lipid membranes with high membrane curvature, and giant unilamellar vesicle (GUV) membranes with negligible curvature. The experimental setup is as referred to in the text (see 38 and 39 for further description). Briefly, a bead (present on the left in each micrograph) with controllable position was specifically adhered to a GUV (visible on the right of each micrograph) and laterally translated to form a tubular membrane connected to the GUV, except in panel g (41). Unless otherwise indicated, GUVs were composed of DOPC with auxiliary lipids mixed at the mole fractions specified, additionally contained Texas Red-DHPE and Biotin-PEG2000-DSPE, and were formed by electroswelling in sucrose solution equi-osmolar to the respective experimental solution conditions. Unless otherwise indicated, each protein shown was conjugated to AlexaFluor 488. The respective references reporting tubulation by these proteins in vitro are included, except for cholera toxin subunit B (CTB), which provides a comparative example. Scale bars (yellow lines) are equal to 3 μm in each micrograph. (a) Drosophila amphiphysin N-BAR (DA N-BAR) (9): 60-nM protein, GUV with 20% DOPS and 12% cholesterol (σ = 0.59 mN m−1), in 1-M sucrose, 15-mM NaCl, and HEPES pH 7.4 (unpublished data from our lab). (b) Rat endophilin A1 N-BAR (6): 150-nM protein, GUV with 25% DOPG (σ = 0.22 mN m−1), in 33-mM NaCl, and HEPES pH 7.4 (unpublished data from our lab). (c) Rgd1 F-BAR [of the SrGAP/Gas7 subfamily (24); see 130]: 190-nM protein, GUV with 40% DOPG (σ = 0.10 mN m−1), in 130-mM NaCl, and HEPES pH 7.4 (unpublished data from our lab). (d) Dynamin (4): conditions as in Reference 43. Images adapted from Reference 43 with permission. (e) Epsin1 ENTH-GFP (8): conditions as in Reference 42 (σ = 0.31 mN m−1) (unpublished data from our lab). (f) Sar1 (13, 132): 1-μM protein (H79G), GUV with 5% DOPS and 10% cholesterol (σ = 0.09 mN m−1), in 2-mM GTP, 9-mM KOAc, 2.5-mM Mg (OAc)2, 2.5-mM EDTA, and HEPES pH 7.2 (unpublished data from our lab). (g) ArfGAP1: conditions and tubule formation as described in Reference 41. Images adapted from Reference 41 by permission from Macmillan Publishers Ltd: The EMBO Journal, copyright 2010. (h) α-synuclein (22): 0.5-μM protein, GUV with 50% DOPG (σ = 0.36 mN m−1), in PBS (unpublished data from our lab). (i) CTB: conditions as in Reference 38 (σ = 0.04 mN m−1). Images adapted from Reference 38, copyright 2009, with permission from Elsevier.

In all cases shown in Figure 1, tubular membranes were connected to giant unilamellar vesicles (GUVs) with essentially negligible curvature (38, 77). This biophysical setup enables the rapid partitioning of proteins among high and low curvature compartments, and thus the fast establishment of thermodynamic equilibrium, necessary for accurate thermodynamic interpretation of curvature sorting (see below). This assay also provides the possibility for the mechanical characterization of highly curved membranes (43, 44, 46, 78).

For all experimental results shown in Figure 1, GUVs were incubated with protein solution after GUV formation, such that peripheral proteins are expected to bind to the outer membrane leaflet only. Figures 1a–c show curvature partitioning of BAR domain proteins. Representative of the second class, Figure 1_d_ shows curvature partitioning of dynamin (43). We note that work similarly extracting tubules, but from supported (79) or suspended (80) lipid bilayers, has also revealed fluorescence localization of dynamin to regions of high curvature. Figures 1_e_–h show members of the third class defined above, including ENTH (42), ArfGAP (41), Sar1, and α-synuclein. Finally, in contrast to members of the three classes of proteins considered above, bacterial toxins such as cholera toxin [CTB; Figure 1_i_ (38)] and Shiga toxin (81) partition away from regions of high positive MC. Data shown in Figure 1 complement previous qualitative and quantitative experimental observations, which have prompted the ongoing discussion of the mechanisms and molecular features responsible for MC-S&G.

MECHANISMS OF MEMBRANE CURVATURE SENSING AND GENERATION

The Scaffolding Mechanism

MC-S&G often involves locally increased concentrations of peripheral proteins with an intrinsic curvature (47) (see Figure 2_a_). The coatomer complexes COPI and COPII are known to generate spherical curvature, whereas dynamin, as well as BAR domain–containing proteins, are believed to provide scaffolds for cylindrical curvature (1). In particular, the proposal that scaffolding (defined as an imprinting of protein monomer or oligomer intrinsic shape of the membrane-binding surface onto the underlying membrane) is responsible for MC-S&G by BAR domains was prompted by the determination of the Drosophila amphiphysin N-BAR domain crystal structure (9). CryoEM reconstructions have supported this mechanism for the dynamin polymer (7, 11).

Figure 2.

Figure 2

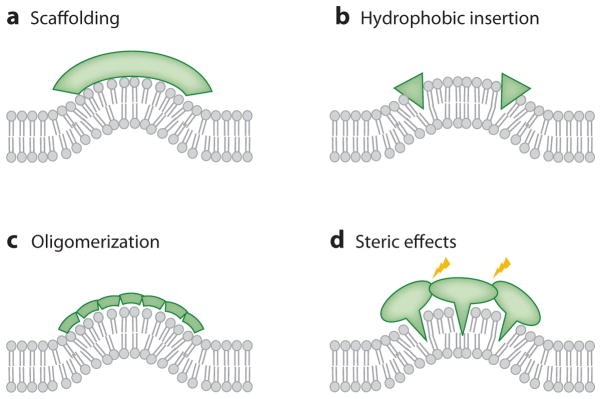
Mechanisms of membrane curvature generation and sensing.

A likely contributor to MC-S&G by N-BAR domains is their N-terminal AH (the feature distinguishing them from classical BAR domains; see below), which may cause tubulation by hydrophobic membrane insertion; this mechanism is discussed in more detail below. Scaffolding, however, is supported by several additional aspects of BAR domain proteins, discussed in the following.

F-BAR proteins (12), which tubulate membranes (see 12, 16, 17, 20) and exhibit a (vesicle-) curvature dependence of tubulation (16) and membrane binding (36), are characterized by larger intrinsic curvature radii than classical BAR and N-BAR domains, as revealed by X-ray crystallography (3, 51). In accordance with predictions of the scaffolding mechanism, EM images show that membrane tubules formed by F-BAR domains generally have larger diameters than do those formed by N-BAR domains (20).

Although, for F-BAR domains, modest (relative to N-BAR domains) insertion of the likely constitutively folded N-terminal helices [e.g., of FCHo2 (17)] and of different nonhelical regions [e.g., in pacsin/syndapin (26, 82)] has been reported, BAR domains can cause membrane tubulation in the absence of hydrophobic insertion. For example, arfaptin, containing a classical BAR domain but lacking membrane-inserting AHs, is able to tubulate membranes (9). Further support for the scaffolding mechanism lies in the importance of the structural rigidity of the endophilin N-BAR domain for its ability to generate curvature, as it has been shown that mutationally compromising N-BAR crescent rigidity negatively affects tubulation (15).

The Role of Helix H0, Hydrophobic Insertion

MC-S&G is also observed for proteins with crystal structures that do not suggest scaffolding, such as the ENTH domain (8). For example, epsin forms an N-terminal α-helix (known as H0) upon PIP2-dependent membrane binding (83). This helix was proposed to insert into the membrane, thereby generating curvature (8) (see Figure 2_b_), and membrane penetration experiments later supported this explanation (29, 33). Also consistent with a role for H0 in MC-S&G is the lack of tubulation following mutations in this region of ENTH (8). Moreover, the structurally similar but not membrane-inserting (83) ANTH domain does not exhibit tubulation (8). Membrane insertion of N-terminal AHs is also believed to be responsible for MC-S&G by Sar1 (13), Arf1 (28), and Arf6 (63), as mutations in their AHs abolish tubulation.

Besides an N-terminal AH, the endophilin BAR domain includes an additional AH that is found within the central region of the dimer (14, 15, 32) that is important for tubulation (14, 15, 84).

Recent research has aimed to assess the relative contributions of scaffolding and hydrophobic insertion. N-BAR domain N-terminal AHs fold upon membrane binding (9, 14, 21, 30, 35, 36) and are termed H0s in reference to the analogous feature of epsin. Mutational deletion of the H0 from the amphiphysin 2 N-BAR domain reduced tubulation of vesicle membranes (9, 30). This finding again indicates that scaffolding can lead to membrane bending in the absence of H0-mediated membrane insertion.

Currently, a generally agreed upon consensus regarding the role of H0s has not been reached. Calculations based on the numerical solution of an analytical continuum mechanics model have suggested conditions in which H0s alone can drive MC (85). However, incubation of vesicles with amphiphysin H0 in the absence of BAR domains was not found to generate significant MC (21). Ineffective tubulation by H0 and curvature generation by BAR and N-BAR are confirmed by recent all-atom and coarse-grained molecular dynamics simulations (86).

Overall, amino acid sequences for AHs of MC-S&G proteins are quite diverse, and the characteristics and mechanisms that distinguish MC-S&G AHs from other membrane-interacting peptides are only beginning to be understood (56). Nonetheless, it is clear that hydrophobic insertion by AHs is an MC-S&G mechanism employed by several proteins. MC-S&G by hydrophobic insertion of nonhelical wedges (18, 23, 25, 26, 31, 87) of proteins has also been characterized.

Membrane Protein Oligomerization Can Cooperatively Amplify Curvature Sensing

For lipids, quantitative experimental evidence (39, 40) has shown, in combination with analytical thermodynamic/mechanical models, that cooperativity (see Figure 2_c_) can amplify curvature sorting (40). The association of F-BAR domain dimers into filaments leads to striated, lattice-like protein coats on lipid tubes (16, 20). The efficacy of such amplification of MC sensing is further underscored by the dependence of dynamin polymerization on MC (43). EM imaging (5, 6, 9, 27) and molecular dynamics simulations (88) suggest that endophilin and amphiphysin proteins and N-BAR domains also oligomerize on tubulated membranes. H0s of these proteins may be involved in this oligomerization, as an amphiphysin H0 has been shown to form an antiparallel dimer in the membrane (21). H0-mediated oligomerization has also been suggested to contribute to MC-S&G for the nonscaffolding ENTH domain (33). Furthermore, it is likely that protein-protein interaction domains, such as SH3 domains, are involved in modulating oligomerization (5, 14) and MC-S&G (15, 82). We note that the formation of oligomerized molecular networks on tubes (with only one nonzero principal curvature) is almost certainly perturbed on spherical vesicles with high MC. Finally, curvature-mediated indirect protein-protein interactions leading to clustering and amplification of MC sensing have also been demonstrated (89).

Nonspecific Steric Interactions Affect Membrane Curvature Sensing and Generation

It has previously been hypothesized (2, 90), and more recently suggested by experiments (91), that local crowding (see Figure 2_d_) of peripheral proteins can cause membrane bending. In these experiments, only when local protein concentration was increased as a result of lipid-based phase separation was tubulation observed. In this study, proteins were used that are known to lack intrinsic curvature (i.e., scaffolding) effects, membrane-inserting AHs, or a tendency for oligomerization (91). Bending by crowding therefore has to be considered as a synergistic contributor to MC-S&G.

CURVATURE SENSING IN MEMBRANE TUBES AND VESICLES: THEORY AND EXPERIMENTS

The curvature-sensing mechanisms described above have not yet been exhaustively considered in thermodynamic/mechanical models. However, several simplifying models analytically describing MC-S&G have been developed. We divide the following discussion of experiments and analytical models for MC-S&G into two sections. In the first section, curvature-sensing molecules are assumed to be present in sufficiently small amounts as to permit the approximation of their mutual interactions on the membrane surface in terms of an ideal two-dimensional gas. Furthermore, in this quasi-infinite dilution regime, it will be assumed that the locally varying concentration of curvature-partitioning molecules does not significantly affect local membrane shape (i.e., this regime is characterized by the absence of significant curvature generation). In the second section, we consider a situation in which membranes are measurably deformed by curvature-partitioning molecules, where linear curvature-composition coupling is found. Situations of nonlinear curvature-composition coupling underlying MC-S&G are likely to exist but have not sufficiently been characterized.

Helfrich-Type Thermodynamic Curvature Sorting Model

Relatively simple thermodynamic/mechanical theories of membrane component (including lipids and proteins) sorting through curvature can be derived from free energy expressions for membrane elasticity, amended by thermodynamic terms that account for free energy contributions from mixing thermodynamics. If we consider a binary mixture of membrane components with differing molecular (intrinsic) spontaneous curvatures, the overall spontaneous curvature Cs as a function of membrane composition is typically expressed as a linear combination of the molecular spontaneous curvatures Ci:

where ϕα and ϕβ are the mole fractions of a binary mixture (ϕα + ϕβ = 1). The spontaneous curvature model may capture the mechanism of scaffolding discussed above. Let us consider the following Helfrich-type (92) free energy functional for an arbitrarily shaped piece of membrane:

F=∫dA{12κ(2H-Cs)2+σ+kBTρ(ϕαlnϕβ+ϕβlnϕβ)}, (2)

where integration is performed over the entire membrane surface A, κ is the bending modulus, H is the mean curvature [i.e., H = 1/2 (_C_1 + C_2), where Ci are principal curvatures], σ is the membrane tension, kB is the Boltzmann constant, T is temperature, and ρ is an area density. For axially symmetric membranes, the principal curvatures further simplify (see below). In the case of membranes with cylindrical shape, one of the principal curvatures vanishes, and the second one is merely the inverse of the cylinder radius Rt : 2_H = Ct = 1/Rt, as measured from the bilayer midplane. From Equation 2, specialized to the case of tubular membranes, it is possible to derive mechanical and chemical equilibrium equations by minimization with respect to Rt and composition, respectively. The mechanical balance equations are well-known (93). The chemical balance equation yields an expression for the chemical potential of curvature-partitioning molecules. Because in the tubular membrane opposite curvatures are found in each lipid monolayer leaflet of a bilayer membrane, the chemical potential expressions for membrane components will be different in both leaflets. For the outer leaflet, where H = Ho, we have for the chemical potential of component α in the outer monolayer, μαo:

μαo=(∂Fo∂Nαo)Ho,Nβo=κa(2Ho-Cs)ϕβo(Cβ-Cα)+kBTlnϕαo. (3)

Here, Fo is the free energy of the outer monolayer, the molecular area a = 1/ρ, and Nαo is the number of molecules of type α. For component β an equivalent expression is found, such that the diffusion- or exchange-potential μ̄ is obtained:

μ¯o=μαo-μβo=1N(∂F∂ϕα)Ho=κa(2Ho-Cs)(Cβ-Cα)+kBTlnϕαoϕβo. (4)

Based on this equilibrium expression, the local mole fractions of curvature-partitioning molecules can be calculated for several different experimental scenarios. For example, connecting a tubular membrane with curvature Ht to a GUV with (essentially) zero curvature, one obtains the following relationship between vesicle composition and tube composition from equating the exchange potentials of vesicle and tube:

κa(2Hot+Csv-Cst)(Cβ-Cα)=kBTlnϕαovϕβotϕαotϕβov. (5)

Equation 5 shows that, in this simple model, curvature sorting depends on the difference of molecular spontaneous curvatures of the molecular components of the mixture.

For the spontaneous curvature of a molecular component of interest to be measured, such a molecule has to be mixed with a second molecule with known spontaneous curvature. Fluorescence microscopy imaging of lipid bilayer membranes is typically carried out under conditions in which the fluorescent molecule is significantly diluted. Assuming a small mole fraction of a probe molecule with nonzero spontaneous curvature Cα, the mechanical balance equations are well approximated by those appropriate for single-component membranes (of species β) with negligible spontaneous curvature. Additionally neglecting terms quadratic in molecular spontaneous curvatures, Equation 5 significantly simplifies to the following form for the outer leaflet of a tubular membrane connected to a large vesicle reservoir (38):

κaCαkBTRt=lnϕαotϕαov. (6)

Equation 6 reveals the exponential form of the curvature partition coefficient K = ϕt/ϕv. Furthermore, for the small left-hand side of Equation 6, the exponentiated form of Equation 6 can be expanded to yield to first order

ϕαotϕαov=1+κaCαkBTRot. (7)

We return to Equation 7 when comparing the spontaneous curvature model (Equation 2) with a model based on the Leibler curvature-composition coupling coefficient Λ (94) (see below).

Equation 5 can be used to examine the extent to which lipid molecules prefer to localize in the inner versus outer leaflet of highly curved vesicle membranes if lipids are allowed to flip and equilibrate among both leaflets (95). For this case, we take Hov = −Hiv such that, for the large dilution scenario, equating the chemical potentials (Equation 4) for inner and outer leaflet results in

4κaCαkBTRv=lnϕαovϕαiv, (8)

where the ratio of compositions here is the ratio of mole fractions in the outer and inner vesicle leaflet, respectively. We note that for accurate fluorescence-based measurements, it has to be taken into account that after sufficient equilibration time, the outer leaflet of highly curved vesicular membranes contains a larger total amount of lipid molecules, due to the larger membrane area of the outer leaflet (95, 96).

Based on the spontaneous curvature model, Equation 8 predicts that interleaflet lipid sorting in highly curved vesicles is four times more effective compared with lipid sorting among a high curvature tube and a flat reservoir. This is explained by the higher mean curvature of the vesicle compared with a tube of equivalent radius and by the fact that in a vesicle leaflet sorting experiment both compartments are bent, whereas in a tube/GUV sorting experiment only one compartment is bent significantly. Both of these differences contribute a factor of two to Equation 8.

Leibler-Type Curvature Sorting Model

In seminal contributions, Leibler initiated the field of theoretical research into MC coupling to local composition (94, 97). Here we show that the Leibler model, under certain assumptions specified below, is equivalent to the spontaneous curvature model. Leibler’s model can be written in terms of the following free energy functional, which regards a piece of membrane with total area A that is connected to a membrane reservoir with negligible curvature:

F=∫dA{2κH2+2ΛΔϕH+12χ-1Δϕ2+σ}. (9)

Here, Λ is the curvature-composition coupling coefficient, Δ_ϕ_ is the difference between the local composition on the membrane surface and the reservoir composition, and χ is the osmotic compressibility of the membrane mixture. The first three terms in this functional have a straightforward thermodynamic interpretation. κ defines the bending stiffness as the coefficient of a second-order Taylor expansion (about the thermodynamic state of the reservoir) in curvature of the free energy area density, Λ is the cross-coefficient of such an expansion, and _χ_−1 is the coefficient of the second-order expansion in the composition variable; i.e., we have the following definitions of inverse susceptibilities (42):

κ=14A(∂2F∂H2)0,Λ=12A(∂2F∂ϕ∂H)0,andχ-1=1A(∂2F∂ϕ2)0, (10)

where the index indicates that derivatives are to be evaluated for a flat membrane (42, 98). Minimization of Equation 9 with respect to the composition variable leads to the following relation between curvature and composition:

In order to compare this relation with the one found for the spontaneous curvature model in the infinite dilution limit (Equation 7), we assume a tubular membrane of radius Rt in connection with a flat (GUV) reservoir. For such a scenario, the inverse osmotic compressibility (assuming ideal mixing) is

χ-1=ρkBT(1ϕαv+1ϕβv)≈ρkBTϕαv (12)

because the second-order derivative is evaluated at the composition of the reservoir (the vesicle). This equation can be derived from Equation 1 and is correct if terms quadratic in molecular spontaneous curvatures are neglected. With Equation 12, Equation 11 can be written in the form

It follows from comparison of Equations 7 and 13 that, with the identity Λ = −κCα, the Leibler description is identical to the Helfrich model with locally varying spontaneous curvature. Analysis of experimental data from a tube pulling assay with an analytical approach related to Equation 13 has been used to determine the spontaneous curvature of the peripheral membrane-binding protein CTB (38, 39), as well as a green fluorescent protein–labeled ENTH domain (42) (see below).

An expression similar to Equation 7 has been used recently to quantify lipid sorting among leaflets of highly curved vesicles by examining data from fluorescence quenching of lipid flu-orophores specifically incorporated into the outer vesicle leaflet (95). From these quantitative curvature sorting experiments, molecular spontaneous curvatures were determined, in good agreement with spontaneous curvatures measured through alternative techniques (95). In contrast to these findings, two studies using tubular membranes pulled from GUVs previously had reported no measurable evidence for curvature sorting of lipid fluorophores (38, 39) in quasi-single-component membranes. Both the sensitivity of the two different experimental methods and the above-mentioned factor of 4 could explain this difference. Nevertheless, both approaches agreed in the assessment of lipid curvature sensing as ineffective. However, as shown below, cooperative lipid-lipid interactions coupled with phase-coexistence boundaries can amplify curvature sorting of lipids.

Bending Stiffness Sorting Model

In addition to curvature sorting through spontaneous curvature as discussed above, we have recently considered (38, 40) a molecular sorting model based on a composition-dependent bending stiffness (98, 99). In this model, the bending stiffness of a binary mixture is considered a linear combination of inverse molecular bending stiffness (1/κi) contributions:

A derivation based on a composition-dependent free energy functional equivalent to Equation 2 leads, for quasi-infinite dilution of molecule α, to the following expression for the curvature partition coefficient:

K=ϕαϕβ=exp(2κβ2aH2kBT(1κα-1κβ)). (15)

Deviatoric Curvature Contributions

We note that the thermodynamic model of the form of Equation 2 considers entropic contributions in the form of configurational entropy that is accounted for only via a simple lattice model. In experimental membranes, several additional entropic contributions are likely to influence the thermodynamics of curvature sorting. Iglic and colleagues (101) considered that for the crescent-shaped BAR domain proteins, statistical fluctuations of the orientation of molecules with respect to the membrane geometry (defined by the angle ω between a plane containing the crescent-shaped protein and the plane defined by an orthogonal cut through a tubular membrane) affect curvature partitioning. In their model, the elastic energy of a flexible rod-like protein was in the following form:

where κp and Lp are the flexural rigidity and length of the protein, respectively; Cp is the curvature of the crescent-shaped protein; and C is expressed as

where D = 1/2 (_C_1 − _C_2) is the deviatoric curvature (100). Numerical evaluation of a free energy functional for tubular membranes connected to vesicle membranes revealed that consideration of the deviatoric curvature contribution predicts increased curvature sorting (101).

Adsorption-Based Curvature Sensing: Experimental Approaches and Theories

The experimental approaches and theoretical models described above considered lateral partitioning instead of molecular exchange between membrane and aqueous solution. Membrane-solution partitioning has been measured to assess the curvature dependence of lipid, peptide, and protein adsorption to vesicular membranes. Among the most commonly used techniques for this scenario are sedimentation (9, 10, 18, 63) and flotation (68, 70) assays. More recently, fluorescence correlation spectroscopy has been used to assess curvature effects on membrane binding (102). Titration calorimetry has been used to assess thermodynamic aspects of curvature-dependent peptide binding (103). For highly curved vesicles, peptide binding was found to be enthalpy driven, whereas for larger vesicles binding was entropy driven. The free energy of binding was found to be weakly dependent on MC, suggesting that entropy-enthalpy compensation acts in reducing the curvature dependence of membrane binding (103).

Recent measurements of curvature sensing by lipids and peripheral proteins via a novel technique developed by Stamou and colleagues (35, 36, 50) have led to significant insight. In their single liposome curvature (SLiC) assay, curvature sensing is defined as a dependence of the surface density of fluorescent membrane-binding molecules incubated with surface-immobilized extruded vesicles (of naturally varying, submicrometer diameters) on MC. Curvature is assessed for individual vesicles via the integrated fluorescence of a membrane-bound reference fluorophore (104), imaged at a wavelength different from the one chosen for the label of the curvature sensor (35, 36).

The authors observed a significant increase of surface densities with decreasing vesicle diameter for vesicles incubated with fluorescent lipids, peptide AHs, acyl-chain membrane-anchored proteins, and several BAR domains. The authors fitted their measured concentration-dependent surface densities BC of membrane-bound molecules with the following equation:

Here, B_max is the surface density of membrane-bound molecules at saturation, KD is an apparent dissociation constant, and c is the aqueous concentration of membrane-binding molecules. Fits of Equation 18 to experimental data revealed that B_max was strongly dependent on the curvature of immobilized vesicles. In addition to MC, measured surface densities were observed to depend on the solution concentration of membrane-binding molecules, as expected. In contrast, an apparent free energy of binding, as calculated from KD via Δ_G = RT_ln_KD, varied only on the order of kBT over the accessible curvature range. These observations were interpreted as indicating that the curvature dependence of amphiphile adsorption to the membrane surface depends primarily on the density of binding sites, rather than curvature-dependent variations in Δ_G for membrane binding. This conclusion is consistent with the above-mentioned enthalpy-entropy compensation (103).

The SLiC assay has provided different curvature-sensing results (for lipid molecules) compared with measurements using the tube/GUV assay, or a vesicle-based fluorescence quenching assay, as has recently been quantitatively discussed (95). Figure 3 allows a direct comparison of findings from the SLiC assay to results obtained from fluorescence measurements in tubes pulled from GUVs, using the same pair of lipid fluorophores. Whereas the SLiC assay reports significant curvature sensing, no curvature sensing can be detected by the tube assay. Figure 4 illustrates unique features of both assays that may contribute to the observed differences in curvature sensing. Tubular membranes pulled from GUVs are in contact with a membrane reservoir, providing a means for rapid exchange of particles as well as membrane area. Because the outer tube monolayer has a larger radius than the inner layer, a change in the tube curvature is accompanied by intermonolayer sliding that allows for fast relaxation of density differences among outer and inner tube leaflets (105). In the SLiC assay, equilibration of lipid density among inner and outer leaflets can occur by slow lipid flipping only (95). Furthermore, in the tube assay curvature sensing occurs through rapid partitioning among the low-curvature thermodynamic reservoir and the high-curvature tube system, whereas exchange of molecules with the surrounding aqueous solution is likely to be a slow process on the timescale of typical experiments. In the SLiC assay, curvature sensing is defined by the extent to which amphiphilic molecules added to the aqueous solution incorporate into the surface-immobilized vesicles of different sizes. It will be important to assess in future measurements to what extent differently curved vesicles in the SLiC assay obtain a state of thermodynamic equilibrium with respect to the exchange of curvature sensors.

Figure 3.

Figure 3

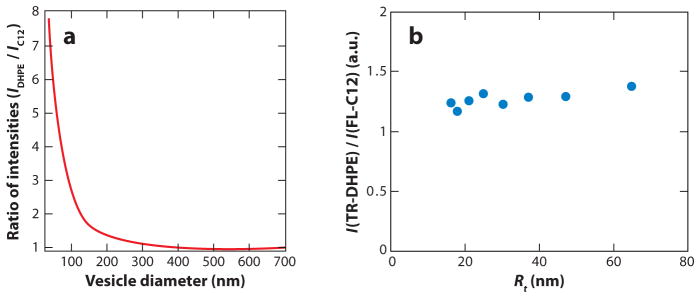
Curvature sensing of fluorescence labeled lipid-like amphiphiles as revealed by (a) the single liposome curvature (SLiC) assay (35) and (b) the tube/giant unilamellar vesicle (GUV) assay (unpublished data from our lab). The comparison employs identical curvature-partitioning molecules [fluorescein-C12 (C12 or FL-C12) and TR-DHPE]. The SLiC assay is described in detail in Reference 35, and the tube/GUV assay is described in Reference 38. Whereas the SLiC assay suggests effective curvature sensing by lipids, the tube/GUV assay does not reveal measurable curvature sorting over the indicated range of tube radii. Panel a adapted with permission from Macmillan Publishers Ltd: Nature Chemical Biology, copyright 2009.

Figure 4.

Figure 4

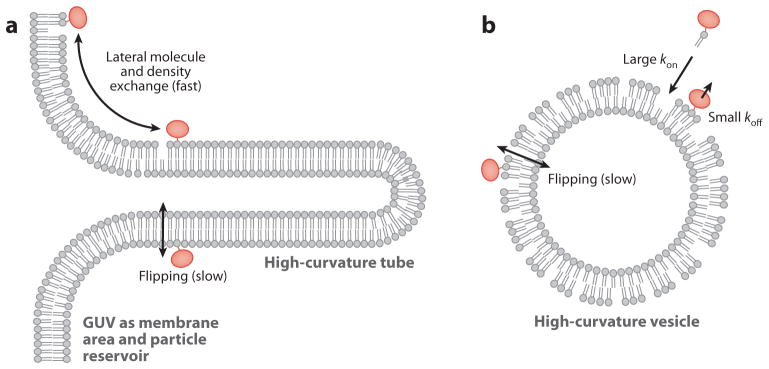
Schematic comparison of (a) the tube/giant unilamellar vesicle (GUV) assay and (b) the single liposome curvature (SLiC) assay. Unique features of the tube/GUV assay are the possibility of rapid equilibration of lipid monolayer density changes associated with tube-curvature changes by membrane area exchange with the large (GUV) membrane reservoir. Furthermore, in the GUV/tube assay the rapid exchange (38) of curvature-partitioning molecules among the tube monolayer and connected GUV monolayer allows rapid thermodynamic equilibration after curvature changes. It is therefore currently unclear to what extent lipid flipping may perturb the interpretation of lipid partitioning data obtained from the tube/GUV assay. Unique to the SLiC assay is that curvature-sensing molecules are added from an aqueous solution to vesicles of different curvatures. It is currently unclear to what extent outer and inner leaflets of vesicles equilibrate during SLiC experiments, and it is unclear to what extent lipid exchange among membranes of different vesicles is a process fast enough to allow for thermodynamic equilibration necessary for analysis with thermodynamic equilibrium models.

We note that Equation 18 is the Langmuir adsorption equation, which is based on the assumption of immobile (distinguishable), noninteracting binding sites. The statistical mechanical description of adsorption onto a mobile surface, however, is known to differ from the functional form of the Langmuir isotherm (106). Furthermore, insertion of amphipathic molecules into a fluid lipid monolayer increases the lateral pressure of the monolayer in a concentration-dependent manner (107). It is therefore likely that membrane-binding sites can be treated as independent only at low binding fractions (BC ≪ _B_max).

Differences in MC sensing by fluorescent lipid-like amphiphiles by methods described above may be reconciled through the development of further refined membrane adsorption models (108–110), the consideration of static and kinetic aspects of the curvature-dependent area and number density of lipid molecules in inner and outer membrane leaflets of vesicles and tubes, and an assessment of the kinetics of the equilibration of area number densities among the outer leaflets of coexisting vesicles in the SLiC assay.

A fluorescence approach similar to the SLiC assay, but with a focus on vesicles with micrometer-scale diameters, recently was used to show that the bacterial peripheral membrane protein SpoVM binds DOPC vesicles in an MC-dependent manner (37). SpoVM consists of 26 amino acids and forms an α-helical structure that inserts into membrane with its long axis parallel to the membrane surface (111). The authors observed the sensitivity of membrane binding to extremely small MC differences and attributed this sensitivity to protein clustering. Cooperative protein-protein interactions were revealed by an influence of protein solution concentration on the measured membrane fluorescence-curvature relations. In addition, the slope of experimental adsorption isotherms was MC dependent. The increase in slope of the isotherms with increasing curvature suggested an enhanced cooperativity of protein binding for vesicles with low diameters. Accordingly, the comparison of experimental data to a thermodynamic membrane adsorption model (109) revealed a strong curvature dependence for the peptide cluster size n, with n < 10 (37). It will be helpful in future research to compare the curvature sensing of SpoVM and the AHs of N-BAR domains studied in the SLiC assay in a similar MC range. However, the available data already suggest that various AHs display substantially different MC-dependent binding, and a detailed description of factors contributing to this complexity is not yet within reach (56).

CURVATURE GENERATION (AND SENSING) IN MEMBRANE TUBES: THEORY AND EXPERIMENTS

In the following we discuss MC generation, in which curvature-sensitive molecules are present in higher concentration compared with those in the high dilution limit theoretically considered above.

Leibler/Spontaneous Curvature Model

Powerful methods to experimentally assess the quantitative mechanical details of the coupling between MC generation and sensing consist of the measurement of (a) the curvature of tubular membranes or (b) the pulling force necessary to mechanically stabilize tubular membranes pulled from GUVs. In order to derive the mechanical balance equations, Equation 2 is specialized to an axially symmetric cylinder with radius Rt, and the resulting simplified functional is minimized with respect to radius, resulting in

κ2Rt2=Λ2χ2Rt2+σ≈Λ2χ2Rt02+σ=Λ2χσκ+σ (19)

after elimination of Δ_ϕ_ by means of Equation 11. In Equation 19, _Rt_0 refers to the equilibrium radius of a membrane with negligible spontaneous curvature, where we have κ/2Rt02=σ. Equation 19 shows that at a given lateral tension σ, the tube radius necessarily shrinks if Λ deviates from zero, regardless of the sign of Λ (94) (i.e., both when the spontaneous curvature of a curvature-sensing molecule is negative and positive). This result is graphically demonstrated by means of computed membrane shapes in Figure 5. The two shapes shown in Figure 5 were calculated by numerically solving the shape equations resulting from Equation 9 (44, 112–116) under boundary conditions that lead to the formation of a tubular membrane suspended from a membrane element with approximate catenoid shape (44, 93, 117). This configuration mimics the shape of tubular membranes suspended from GUVs (see Figure 1). The shapes in Figure 5 were calculated assuming identical parameters and boundary conditions, except that Λ was assumed to be negative for Figure 5_a_, and positive for Figure 5_b_, reflecting curvature-induced preferential partitioning onto and away from the tube, respectively. In both cases, however, the tube curvature is larger compared to a membrane with Λ = 0 (added for comparison to both Figures 5_a_,b). Importantly, curvature generation therefore cannot immediately be related to a local spontaneous curvature; the thermodynamic sorting model indicates that the whole thermodynamic system (tube membrane plus particle and membrane area reservoir) has to be considered in evaluating MC-S&G.

Figure 5.

Figure 5

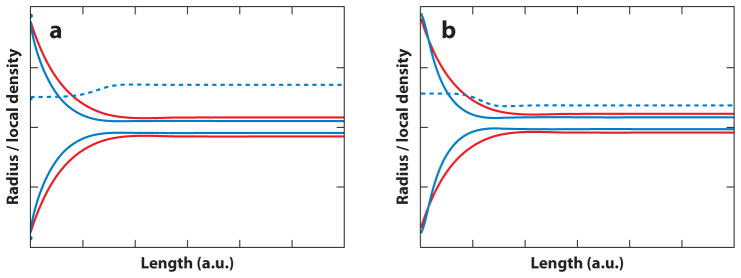
Computed membrane shapes obtained from the numerical integration of differential shape equations assuming boundary conditions that lead to an approximate catenoid shape with low curvature (left in both panels) and a tubular membrane (right in both panels). The shapes in both panels were obtained using identical parameters and boundary conditions (total membrane area A = 4_π_, length of the membrane shape L = 3, and lateral tension σ = 20). (a) Membrane shape (solid blue line) calculated assuming a curvature-composition coupling coefficient of Λ = −0.5, implying positive spontaneous curvature of a curvature-partitioning molecule added at a mole fraction of ϕ = 0.5 in a binary mixture additionally containing a species with negligible spontaneous curvature. Positive molecular spontaneous curvature leads to the enrichment of curvature-partitioning molecules in the outer leaflet of the tubular membrane (dashed blue line). For comparison, a shape has been added that was computed assuming Λ = 0 (solid red line); for vanishing curvature-composition coupling, a larger tube radius is observed. (b) Identical conditions as in panel a except that Λ = 0.5 was assumed, implying negative molecular spontaneous curvature and depletion (dashed blue line) of the curvature-partitioning molecule from the tubular membrane. In this case as well, a thinner tube (blue solid line) is observed compared to a membrane in the absence of curvature partitioning (red solid line).

Equation 19 can be rearranged to yield (39, 42)

1Rt2=2σκ(1+Λ2χκ)≈2σκ-Λ2χ=2σκeff. (20)

From Equation 20, an effective (renormalized) bending stiffness κeff can be defined as (94, 98)

This effective stiffness is observed to always be smaller compared with the bare stiffness in the absence of curvature-sensitive molecules (note that the osmotic compressibility is always positive for homogeneous, i.e., non-phase-separated membranes). Equation 20 determines to what extent curvature-induced repartitioning of curvature-sensing molecules leads to local changes in MC. With Equation 11, an expression is obtained that shows the fundamental coupling between MC sensing and generation:

Because κeff is a quantity that depends on the composition of the thermodynamic reservoir, curvature sorting is amplified if the membrane concentration of curvature-partitioning molecules is large enough to lead to significant membrane deformation. Curvature sensing and curvature generation thus are synergistically coupled phenomena both quantified through the parameter Λ.

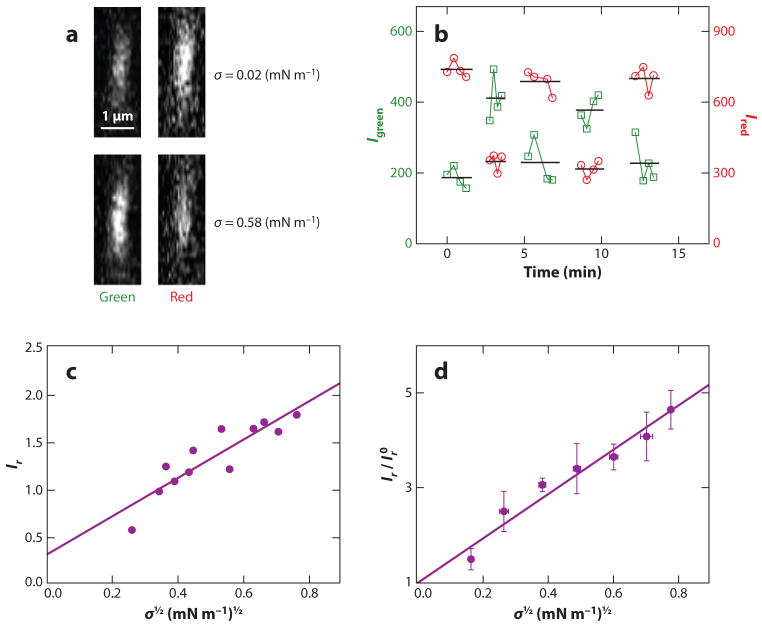
Equation 22 was used to analytically interpret the previously described measurements of curvature partitioning of the ENTH domain (42). Figure 6 shows representative measurements of fluorescence levels of tubular membranes covered with fluorescently tagged ENTH. Confocal fluorescence microscopy tube cross-section images (Figure 6_a_) display fluorescence intensities that change with tube curvature adjusted by changing membrane tension. Whereas ENTH fluorescence is observed to increase with increasing curvature (demonstrating curvature sensing), fluorescence collected by means of a red lipid fluorophore decreases with increasing curvature [reflecting a decreasing imaged tube area (38)]. Fluorescence intensities are observed to reversibly change when membrane tension is cycled (Figure 6_b_). Fluorescence intensity ratios Ir comparing protein and lipid fluorescence show a systematic dependence on MC (Figure 6_c_), as shown for ENTH (42). Similar measurements have also been obtained for the proteins Arf1 and ArfGAP1 (41). The curvature dependence of ENTH partitioning is shown in normalized form in Figure 6_d_. Here, curvature-sorting ratios Ir are displayed relative to values Ir0 obtained from extrapolating to zero curvature linear fits, such as that shown in Figure 6_c_. The slope of Figure 6_d_ can then be related to the curvature-composition coupling constant Λ, according to the following relation:

IrIr0=1-ΛρkBT2σκeff, (23)

which results from Equation 22 by assuming that fluorescence intensities are proportional to mole fractions. Furthermore, for the osmotic compressibility of Equation 22, ideal two-dimensional gas conditions were assumed (Equation 12).

Figure 6.

Figure 6

Quantitative experimental measurements of curvature partitioning based on the tube/giant unilamellar vesicle assay, as demonstrated with the example of ENTH-GFP. (a) Representative tube fluorescence cross-section images comparing ENTH-GFP (green channel of the confocal fluorescence microscope) and lipid dye (red channel) at two different lateral tensions. Whereas ENTH-GFP fluorescence increases with an increase of lateral tension (coupled with an increase in membrane curvature), the lipid fluorescence intensity is observed to decrease with increasing tension as expected (38). (b) Demonstration of reversible fluorescence intensity changes under cycling membrane tension, demonstrating thermodynamic equilibrium conditions necessary for thermodynamic analysis. (c) Relative fluorescence intensity values Ir (expressed as protein versus lipid fluorescence) as a function of applied membrane tension of a tubular membrane. An approximately linear relationship is obtained. (d) The intercept resulting from extrapolation to zero tension is used to normalize multiple data sets. The slope of this graph can be related to the curvature-composition coupling coefficient Λ (42). For further details, we refer readers to Reference 42. Adapted with permission from Reference 42. Copyright 2010 American Chemical Society.

Bending Stiffness Model

From the discussion above it is clear that spontaneous curvature (nonzero Cα and therefore Λ) is an important mechanism for MC generation and leads to renormalization of the effective bending stiffness. A second mechanism that leads to the reduction of effective bending stiffness is encountered if the bending stiffness depends on membrane composition even in the absence of spontaneous curvature. Recently, it has been demonstrated that the peripheral protein Sar1 causes softening of the lipid bilayer (45). The authors developed a mechanical model to interpret their experimental findings. In the following, we discuss how mechanical models that consider membrane-composition-dependent bending stiffness can be amended by thermodynamic contributions arising from the free energy of mixing.

To thermodynamically investigate the contribution of a composition-dependent bending stiffness to MC generation in tubular membranes, one must expand the free energy of the tubular membrane to third order. In recently published models (39, 40), the following mixed derivatives have been considered:

ρ4(∂2μ¯∂H2)=(∂κ∂ϕα)≡Ω. (24)

Both the left- and right-hand sides of Equation 24 represent third-order derivatives of the tube’s free energy (second order in curvature, and first order in composition of a membrane consisting of a binary mixture of molecules α and β). For this model, the equivalent to Equation 9 can be written as

F=∫dA{2κH2+2ΩϕH2+12χ-1Δϕ2+σ}. (25)

Expressing this free energy for tubular membranes, and minimizing with respect to the composition change, yields the following relation between tube composition and its curvature:

With the help of this expression, the composition dependence can be eliminated from Equation 25. The resulting free energy can then be minimized with respect to curvature to yield

σ=κ2Rt2-3χΩ28Rt4≡12κeffRt2. (27)

Equation 26 thus defines an effective stiffness for curvature sorting based on composition-dependent stiffness:

This renormalized stiffness expression is similar in form compared with Equation 21. The main difference is that the effective bending stiffness of Equation 28 depends on MC. Measurements of tube radius as a function of applied membrane tension σ have recently been used to determine the product of thermodynamic derivatives in Equation 27 (40). Alternatively, pulling-force measurements as a function of applied membrane tension, in conjunction with a formalism equivalent to the one just outlined, have been performed to evaluate the strength of curvature-composition coupling in membrane with composition-dependent bending stiffness (39). Both studies showed experimentally that curvature sorting becomes increasingly more efficient near the critical point (118) of the lipid mixture phase diagram (39, 40). This experimental observation has previously been theoretically predicted (94, 119).

CONCLUDING REMARKS

The quantitative understanding of MC-S&G currently is quickly evolving, with both new and established methods advancing the field. We have reviewed relatively simple thermodynamic models that can serve as a starting point for analysis of experimental measurements. Clearly, the multitude of different mechanisms for MC-S&G discussed is not yet sufficiently reflected in analytical models presented here. We note that substantially more sophisticated models have been developed based on statistical mechanical and mechanical models that consider the molecular details of lipids and proteins (85, 120–124). Our understanding of MC-S&G will critically rely on the synergy between these models and quantitative experiments, increasingly in connection with molecular dynamics simulations (84, 86, 125).

SUMMARY POINTS.

  1. Classes of proteins involved in MC-S&G can be distinguished based on their molecular structure and include BAR domain proteins, dynamin family proteins, and proteins with amphipathic, membrane-inserting helices or loops in the absence of a rigid membrane-binding scaffold.
  2. Mechanisms that are likely to contribute to MC-S&G by peripheral membrane proteins include scaffolding, hydrophobic insertion, oligomerization, and steric protein-protein interactions.
  3. Simple thermodynamic models have been developed and fitted to experimental observations in the form of quantitative measurements of curvature partitioning and mechanical equilibria.

FUTURE ISSUES.

  1. We suggest that an area warranting further attention is a systematic investigation of contributions of the lipid host matrix (126) to quantitative aspects of MC-S&G by peripheral proteins. Potentially important features include head group size, degree of tail unsaturation, electrostatic aspects (127), and cholesterol content.
  2. Secondly, it will be important in quantitative assessments of experimental model systems to consider MC-S&G being modulated by heteromeric protein-protein interactions, such as those involving specific protein-protein interaction domains (82).
  3. A third aspect of importance to the field will be the continued improvement of analytical thermodynamic models. This will likely include models that consider attractive and repulsive homomeric protein-protein interactions and theories based on bilayer coupling models (128–130).
  4. Finally, it is likely that dynamic aspects (41, 44) of MC-S&G will receive increasing attention.

Acknowledgments

We apologize to all investigators whose research could not be cited owing to space limitations. We extend special thanks to our collaborators for the donation of fluorescently labeled proteins and many fruitful discussions: M. Aridor, W. Cho, R. Langen, M. Lemmon, E. Rhoades, M. von Zastrow, and T. Lubensky. We furthermore acknowledge stimulating discussions with D. Stamou and thank M. Heinrich for a careful reading of the manuscript. Funding was provided by the NSF and the AP Sloan Foundation.

Glossary

MC

membrane curvature

Curvature sensing

curvature-dependent membrane-binding affinity of a molecule

Curvature generation

membrane deformation through local enrichment of curvature-sensing molecules

MC-S&G

membrane curvature sensing and generation

EM

electron microscopy

Bin/Amphiphysin/ Rvs (BAR) domain

crescent-shaped protein domain involved in curvature sensing and generation

N-BAR

BAR domain with N-terminal helix

Scaffolding

mechanism of curvature generation by imprinting intrinsic shape of a protein

AH

amphipathic helix

ENTH

epsin N-terminal homology domain

Micropipette aspiration

biophysical technique allowing mechanical manipulation of giant unilamellar vesicles; in particular, membrane tension can be hydrostatically regulated

Giant unilamellar vesicle (GUV)

self-assembled lipid bilayer model membrane with spherical topology

Hydrophobic insertion (wedging)

mechanism of curvature sensing/ generation involving perturbation of lipid density through interaction of proteins with hydrophobic lipid components

Membrane tube/ tether

cylindrically shaped lipid bilayer membrane with essentially length-independent curvature with typical curvature radii between 10 and 500 nm

Spontaneous curvature

curvature of a membrane-binding interface, or of a membrane itself, in the absence of any external stresses

SLiC

single liposome curvature assay

Footnotes

DISCLOSURE STATEMENT

The authors are not aware of any affiliations, memberships, funding, or financial holdings that might be perceived as affecting the objectivity of this review.

Contributor Information

Tobias Baumgart, Email: baumgart@sas.upenn.edu.

Benjamin R. Capraro, Email: capraro@sas.upenn.edu.

Chen Zhu, Email: chenzhu@sas.upenn.edu.

Sovan L. Das, Email: sovandas@iitk.ac.in.

LITERATURE CITED