differensialregning – Store norske leksikon (original) (raw)
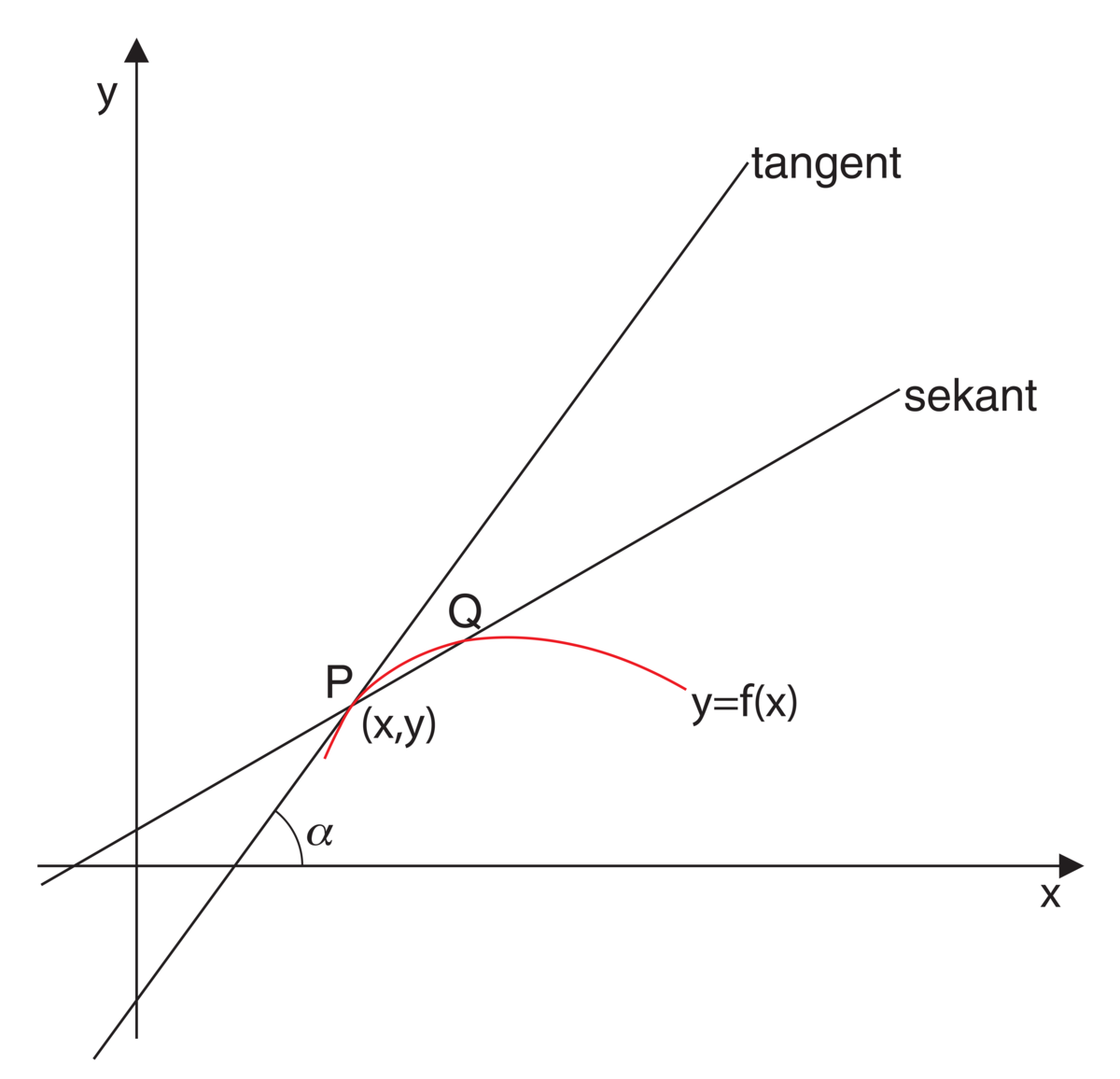
Differensialregning Det grafiske bildet av funksjonen y = f(x) i et rettvinklet koordinatsystem. Se for øvrig artikkelteksten.
Differensialregning er et område innen matematikken som tar for seg fenomener som karakteriseres ved endring. Endringen kan for eksempel være bevegelse eller akselerasjon, som i mekanikken, eller utvikling og vekst, som i biologien. Hastigheten er den deriverte av posisjonen, og akselerasjon er den deriverte av hastigheten (se nedenfor).
Faktaboks
Uttale
differensiˈalregning
Derivasjon
Hvis en matematisk funksjon beskriver hvordan et visst fenomen forandrer seg med tiden, vil den deriverte funksjonen være et uttrykk for hvor hurtig denne forandringen skjer i hvert øyeblikk. For funksjonen \(y=f(x)\) er symbolet for den deriverte funksjonen enten \(y'\) eller \(f'(x)\). Om en bil kjører langs en rett vei, og \(y=f(x)\) er posisjonen til bilen ved tiden \(x\), vil \(y'=f'(x)\) være hastigheten til bilen ved tid \(x\) slik den kan leses av på speedometeret. Dersom man deriverer \(y=f(x)\) to ganger, vil det gi bilens akselerasjon ved tiden \(x\).
Analytisk definisjon
Går man ut fra en verdi av \(x\) med tilhørende funksjonsverdi \(f(x)\), og tenker seg at \(x\) får et tillegg \(h\) (positivt eller negativt), slik at funksjonsverdien blir \(f(x+h)\), vil den deriverte funksjonen \(f'(x)\) være definert som grenseverdien for uttrykket \(\frac{f(x+h)-f(x)}{h}\) når h nærmer seg null.
I matematisk tegnspråk kan man uttrykke dette slik: \[f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}.\] Ordet lim er forkortelse for limes (latin 'grense').
Geometrisk definisjon
Den deriverte funksjonen \(f'(x)\) kan også defineres ut fra en rent geometrisk betraktningsmåte ved å se på kurven for funksjonen \(y=f(x)\) i et rettvinklet koordinatsystem med horisontal \(x\)-akse og vertikal \(y\)-akse, og på den vinkel tangenten i et kurvepunkt danner med _x_-aksen.
For en sirkel er tangenten definert som en rett linje som bare har ett punkt felles med sirkelen, og en slik definisjon kan også brukes for andre enkle kurver. Men for mer kompliserte kurver blir tangenten definert ved en grensebetraktning: Tangenten til en kurve i et punkt \(P\) på kurven, er grensestillingen for sekanten man kan trekke gjennom \(P\) og et annet punkt \(Q\) på kurven når \(Q\) nærmer seg mot \(P\) (under forutsetning av at den gitte kurven er av en slik art at denne grenseovergangen har mening). I så fall vil tangenten i punktet \(P(x,y)\) på kurven danne en vinkel \(\alpha\) med _x_-aksen slik at \(\tan\alpha=f'(x)\).
I geometrisk formulering er derfor differensialregningens grunnproblem å bestemme tangens til en tangents vinkel med _x_-aksen, fordi denne verdien er et uttrykk for vinkelens størrelse, og dermed et uttrykk for hvor hurtig funksjonen vokser eller avtar i tangeringspunktet.
Selve operasjonen som består i å finne den deriverte funksjon \(f'(x)\), kalles å derivere eller differensiere funksjonen. Den deriverte behøver imidlertid ikke alltid å eksistere, selv om \(f(x)\) er en kontinuerlig funksjon og geometrisk derfor er en sammenhengende kurve. En funksjon som har en derivert kalles deriverbar eller differensierbar.
Derivasjonsregler
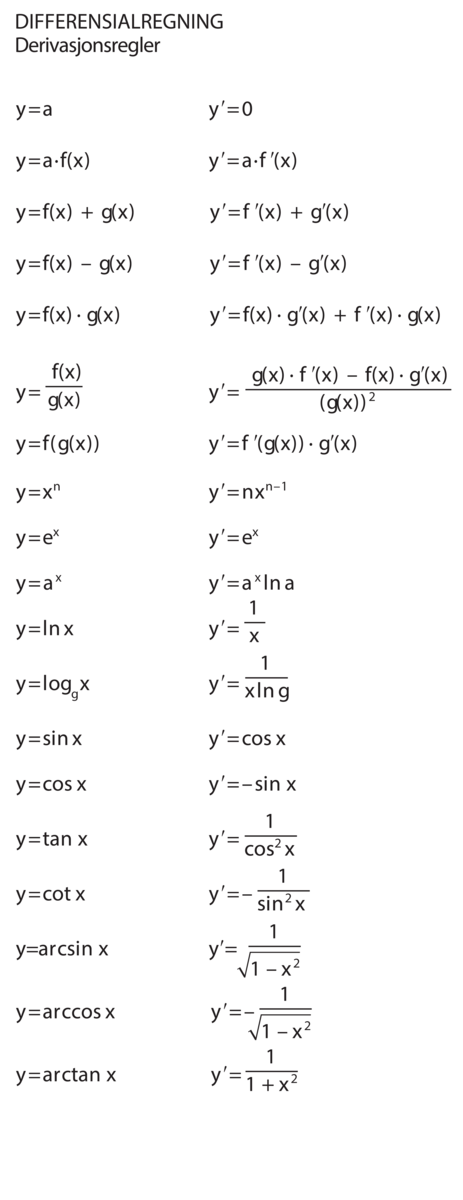
Noen viktige derivasjonsregler.
For derivering har man en rekke generelle regler. Den deriverte av summen av to funksjoner \(y = f(x) + g(x)\), er \(y' = f' (x) + g '(x)\), og den deriverte av produktet av to funksjoner \(y = f(x) \cdot g(x)\) er \(y ' = f(x) \cdot g '(x) + g(x) \cdot f '(x)\), den såkalte Leibniz' regel. Sammen med kjennskapet til den deriverte av en rekke spesielle funksjoner som for eksempel \(x^n\), \(\sin x\) og \(\cos x\), gjør disse regler at vi kan finne uttrykk for de deriverte funksjoner som opptrer i forskjellige anvendelser. Se for øvrig tabell med noen derivasjonsregler.
I stedet for \(y'\) og \(f'(x)\) bruker man også symbolet \(\frac{dy}{dx}\) hvor bokstaven \(d\) står for ordet differensial. Symbolet må imidlertid ikke oppfattes som en brøk i vanlig forstand.
Det er ofte hensiktsmessig å derivere en funksjon to eller flere ganger på rad. Den første deriverte blir da \(f'(x)\), den andre deriverte \(f''(x)\) og så videre. Om vi deriverer funksjonen \(n\) ganger, kan vi skrive det som \(y^{(n)}\) eller \(f^{(n)}(x)\).
Er en funksjon avhengig av to variabler, for eksempel \(z=f(x,y)\), kan det oppstå behov for å derivere funksjonen under den forutsetning at for eksempel \(y\) er konstant og \(x\) variabel. Da skriver man ofte resultatet slik: \(\frac{\partial f}{\partial x}\) og leser: den partiellderiverte av \(f\) med hensyn på \(x\). Om man partiellderiverer to ganger med hensyn på \(x\), skriver man dette som \(\frac{\partial^2 f}{\partial x^2}\). Dersom man istedenfor partiellderiverer én gang med hensyn på \(x\) og én gang med hensyn på \(y\), skriver man dette som \(\frac{\partial^2 f}{\partial y \partial x}\). Om funksjonen \(f\) er tilstrekkelig regulær, vil \[\frac{\partial^2 f}{\partial y \partial x}=\frac{\partial^2 f}{\partial x \partial y},\] det vil si at det ikke betyr noe i hvilken rekkefølge man foretar derivasjonene. Det er også vanlig å bruke indekser til å angi partiellderivasjon, dvs \(f_{xy}=\frac{\partial^2 f}{\partial y \partial x}\).
La oss se på eksemplet \(z=f(x,y)= x^2y^3+\sin(xy)+x+2y\). Da er \(z_x=f_x(x,y)= 2 xy^3+y\cos(xy)+1\) og \(z_y=f_y(x,y)= 3 x^2y^2+x\cos(xy)+2\). For de andrederiverte finner vi \(z_{xx}=f_{xx}(x,y)= 2 y^3-y^2\sin(xy)\), \(z_{yy}=f_{yy}(x,y)= 6 x^2 y-x^2\sin(xy)\) og \(z_{xy}=f_{xy}(x,y)= z_{yx}=f_{yx}(x,y)=6 x y^2-xy\sin(xy)\).
Historikk
Allerede i gresk matematikk var det tilløp til en problembehandling som man nå vil regne til differensialregningen. Mer direkte forløpere til differensialregningen finner man på 1500- og 1600-tallet, særlig navn som Bonaventura Cavalieri, Johannes Kepler og Pierre de Fermat.
Det er imidlertid Isaac Newton og Gottfried Wilhelm von Leibniz som regnes som de egentlige grunnleggere av dagens differensialregning, som sammen med integralregning inngår som en vesentlig del i mange grener av matematikken og i matematisk betonte vitenskaper, for eksempel fysikk, astronomi, statistikk og samfunnsøkonomi.