eksponentiell – Store norske leksikon (original) (raw)
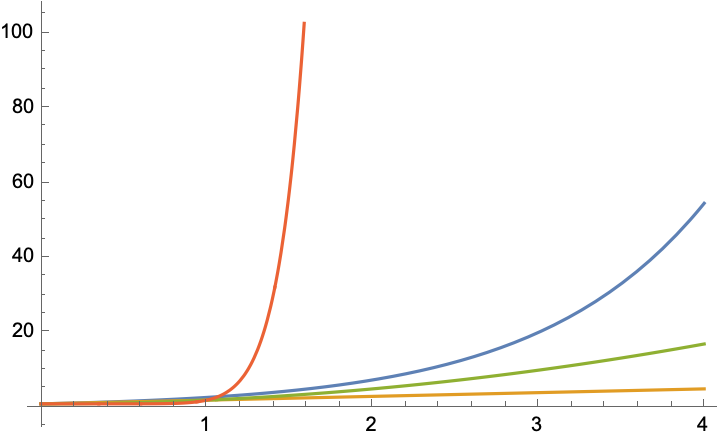
Figuren viser funksjonene \(x+1, x^2+1, x^{10}+1\) samt \(e^x\) (rød kurve).
Eksponentiell refererer til mange ulike begreper som er relatert til eksponensiering.
Faktaboks
av latin
Også kjent som
eksponential
Eksponentiell vekst
Vi snakker om eksponentiell vekst av en størrelse dersom veksten i ett øyeblikk er proporsjonal med verdien av størrelsen i det samme øyeblikket.
Et eksempel er vekst av bakterier. Om én bakterie deler seg i to hvert minutt, vil vi etter ett minutt har to bakterier, etter to minutter ha fire bakterier, etter tre minutter ha åtte bakterier og så videre. Etter \(n\) minutter vil det være \(2^n\) bakterier. Vi kan skrive det som \(2^n=e^{n \ln 2}\) der \(e\) er Eulers tall \(e\) og \(e\approx 2,71828\) er grunntallet for eksponentialfunksjonen. Renters rente gir også opphav til eksponentiell vekst.
I dagligtalen brukes ofte eksponentiell vekst i en mindre presis betydning som en betegnelse på en svært sterk vekst.
Kontinuerlig vekst
For kontinuerlig vekst får vi følgende situasjon. La \(y=f(x)\) betegne mengden av størrelse ved tiden \(x\). Veksten av denne størrelsen ved tiden \(x\) er gitt ved den deriverte av \(y\), som vi skriver som \(y'\). Om veksten skal være proporsjonal med mengden vi har, må \(y\) tilfredsstille differensialligningen \(y'=ky\), der \(k\) er proporsjonalitetskonstanten. Denne ligningen har løsningen \(y=f(x)=Ae^{kx}\) der \(e^x\) betegner eksponentialfunksjonen og \(A\) er en vilkårlig konstant som er gitt ved verdien av størrelsen ved tiden \(x=0\), det vil si \(A=f(0)\).
Ofte settes eksponentiell vekst opp mot polynomisk vekst der en størrelse vokser som \(Cx^N\) for en konstant \(C\) og et fast tall \(N\). Uansett størrelse på disse konstantene vil alltid eksponentiell vekst være mye større i det lange løp. Se figur.