differensialligning – Store norske leksikon (original) (raw)
Differensialligning er en matematisk ligning som inneholder både en funksjon og en eller flere deriverte av denne funksjonen. Differensialligninger er en sentral del av matematisk analyse og brukes til å beskrive og løse en lang rekke viktige problemer på de fleste områder innen naturvitenskap og teknologi.
Faktaboks
Uttale
differensiˈalligning
Eksempler
En enkel differensialligning er \[y'=y\] som beskriver eksponentiell vekst. Den har løsning \[y=y(x)= c e^x\] der \(c\) er en vilkårlig konstant og \(e^x\) er eksponentialfunksjonen. Om vi kjenner verdien av \(y(x)\) for én verdi av \(x\), kan vi bestemme verdien av konstanten \(c\). Dersom vi for eksempel vet at \(y\) er \(y_0\) for \(x=0\), det vil si \(y(0)=y_0\), så vil \(y(x)= y_0 e^x\) være løsningen av differensialligningen.
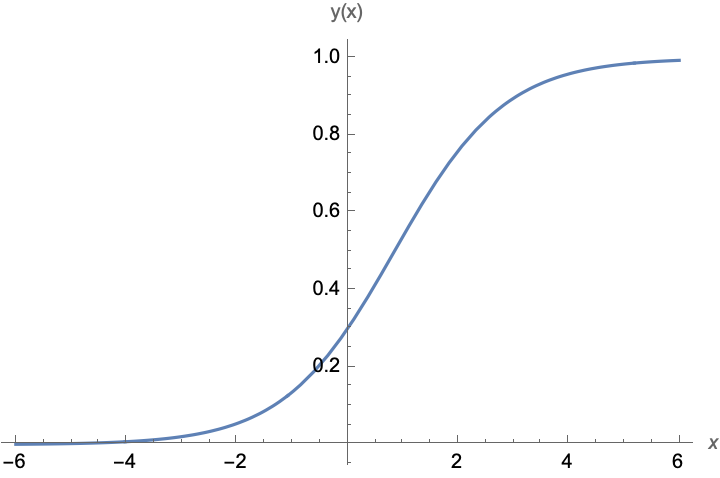
Et annet eksempel er den logistiske ligningen \(y'=y(1-y)\) som kan brukes til å beskrive veksten til en populasjon. Den har løsning \(y=y(x)=1/(1+c e^{-x})\) der \(c\) er en konstant. Om populasjonen er \(y_0\) ved tiden \(x=0\), det vil si at \(y(0)=y_0\), blir \(c=(1-y_0)/y_0\), og løsningen kan skrives som \[y(x)= \frac{y_0}{y_0+(1-y_0)e^{-x}}.\] Om \(y_0\in [0,1]\), vil også løsningen være mellom 0 og 1, det vil si at \(y(x)\in [0,1]\). Kurven vil flate ut når \(x\) vokser, og vi har at \(y(x)\to 1\) når \(x\to\infty\). Det betyr at \(y=1\) er en asymptote for funksjonen.
Løsninger av differensialligninger
Hvis \(y^{(n)}\) er den høyeste deriverte som forekommer, sies differensialligningen å være av \(n\)'te orden. Ligningene overfor er begge av første orden.
Bestemmelsen av alle funksjoner \(y\) som tilfredsstiller en differensialligning, kalles å løse ligningen. I alminnelighet er ikke løsningen entydig bestemt, men avhenger av visse konstanter, slik vi så i eksemplene ovenfor. Differensialligningen \[y''+y=0,\] som er av andre orden, har løsningen \(y=y(x) = c_1 \cos x + c_2 \sin x\) hvor \(c_1\) og \(c_2\) er vilkårlige konstanter. Disse kan bestemmes om vi for eksempel kjenner \(y\) og \(y’\) i ett punkt, for eksempel \(x=0\). Om \(y(0)=y_1\) og \(y’(0)=y_2\), blir \(c_1=y_1\) og \(c_2=y_2\), og løsningen kan skrives \[y(x) = y_1 \cos x + y_2 \sin x.\]
Det er bare de aller færreste differensialligninger som har eksplisitte løsninger som eksemplene ovenfor. For å kunne finne en løsning må man derfor ofte benytte metoder fra numerisk analyse og beregne løsningene på datamaskiner. Disse løsningene vil være tilnærmede og ikke eksakte løsninger.
Ulike typer differensialligninger
Tradisjonelt skiller man mellom to typer av differensialligninger, nemlig ordinære og partielle differensialligninger.
Ordinære differensialligninger
For de ordinære differensialligningene er det én fri (også kalt uavhengig) variabel. I eksemplene ovenfor er \(x\) denne frie variabelen. Newtons gravitasjonslov er et annet eksempel på en ordinær differensialligning der den frie variabelen er tid, og der størrelsene som skal bestemmes for eksempel kan være planetenes posisjon som funksjon av tiden.
Partielle differensialligninger
Dersom det er mer enn én fri variabel, er det snakk om en partiell differensialligning. De uavhengige variablene kan være tid og rom (én eller flere dimensjoner). Da trenger man å benytte partiellderiverte.
Mange naturlover er beskrevet ved partielle differensialligninger: Maxwells ligninger for elektromagnetisme, Schrödinger-ligningen for kvantemekanikk, den generelle relativitetsteorien samt Navier-Stokes-ligningene for væsker er alle partielle differensialligninger. Her er de uavhengige variablene tid og tre romdimensjoner, dvs fire uavhengige variable.
Klassiske partielle differensialligninger
De tre klassiske partielle differensialligningene er bølgeligningen, varmeledningsligningen og Laplaces ligning.
- Bølgeligningen beskriver for eksempel utslaget av en gitarstreng. Om \(u\) er utslaget og \(x\) er posisjon på strengen og \(t\) er tiden, vil utslaget \(u=u(t,x)\) oppfylle den partielle differensialligningen \[\frac{\partial^2 u}{\partial t^2}-\frac{\partial^2 u}{\partial x^2}=0.\]
- Varmeledningsligningen kan beskrive temperaturfordelingen for eksempel i en jernstang. Om \(u=u(t,x)\) betegner temperaturen i et punkt \(x\) i stangen ved tiden \(t\), vil temperaturutviklingen være bestemt ved den partielle differensialligningen \[\frac{\partial u}{\partial t}-\frac{\partial^2 u}{\partial x^2}=0.\]
- Laplaces ligning kan beskrive fenomener der vi har et potensial. For stasjonær flyt av en inkompressibel væske har vi et potensial \(V=V(x,y,z)\) slik at hastigheten \(u\) av væsken er gradienten til \(V,\) det vil si at \(u =\nabla V\), og \(V\) vil oppfylle ligningen \[\Delta V=0\] der \(\Delta\) er Laplace-operatoren og gitt ved \(\Delta V= \frac{\partial^2 V}{\partial x^2}+\frac{\partial^2 V}{\partial y^2}+\frac{\partial^2 V}{\partial z^2}\).
For å kunne løse en partiell differensialligning, må man kjenne rand- og initialverdiene til den ukjente funksjonen. For bølgeligningen som model for en gitarstreng betyr det følgende: Vi må vite hvordan vibrasjonene startet (hvor mye trakk vi strengen ut, og ga vi den en dytt?) – initialbetingelser – og hvordan strengen er festet på endene – randbetingelser. Om vi kjenner disse, har bølgeligningen en éntydig løsning.
Om det er flere ukjente funksjoner, snakker man om systemer av differensialligninger. I hvert av de konkrete eksemplene ovenfor er det bare én ukjent funksjon. Slike ligninger kalles skalare differensialligninger. Newtons gravitasjonslov, der hver planets posisjon representerer én ukjent funksjon er et eksempel på et system av ordinære differensialligninger.
Man skiller også mellom lineære og ikke-lineære differensialligninger. I en lineær differensialligning forekommer den ukjente funksjonen og alle dens deriverte bare lineært. Om ligningen i tillegg er homogen, vil det såkalte superposisjonsprinsippet gjelde, det vil si at at om man har to løsninger, vil også summen av de to løsningene være en løsning av ligningen. Om ligningen ikke er lineær, er den ikke-lineær. Alle de tre klassiske partielle differensialligningene ovenfor er lineære. Videre er Schrödinger-ligningen lineær, mens både Newtons gravitasjonslov, den generelle relativitetsteorien og Navier–Stokes ligningene er ikke-lineære.
Historikk
Løsning av differensialligninger var en av de første anvendelser av integralregningen både hos Isaac Newton og Wilhelm Leibniz. Teorien ble senere utviklet av en rekke matematikere, spesielt kan nevnes Johann Bernoulli og Leonhard Euler. Den norske matematikeren Sophus Lie gjorde banebrytende arbeider over gruppeteoriens anvendelse på differensialligninger.
Teorien for differensialligninger er nå et av de viktigste områdene i matematikk og det mest sentrale hjelpemidlet i anvendt matematikk, og i de fleste områder av naturvitenskap og teknologi, for eksempel i mekanikk, fysikk, kjemi, biologi, elektroteknikk, ingeniørfag og økonomi.