Теорема Гаусса — Ванцеля | это... Что такое Теорема Гаусса — Ванцеля? (original) (raw)

Теорема Гаусса — Ванцеля

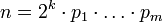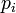Теорема Гаусса — Ванцеля утверждает, что правильный _n_-угольник возможно построить с помощью циркуля и линейки тогда и только тогда, когда $n=2^k\cdot p_1\cdot \ldots \cdot p_m$ , где $p_i\,\!$ — различные простые числа Ферма. Это условие также эквивалентно тому, что значение функции Эйлера 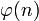$\varphi(n)$ является степенью 2-ки.

История

Античным геометрам были известны способы построения правильных _n_-угольников для n = 2k, 3·2k, 5·2k и 3·5·2k.

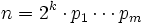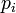Гаусс показал в 1796 возможность построения правильных _n_-угольников при $n=2^k\cdot p_1\cdots p_m$ , где $p_i\,\!$ — различные простые числа Ферма. В 1836 Ванцель доказал, что других правильных многоугольников, которые можно построить циркулем и линейкой, не существует.

Конкретные реализации построения весьма трудоёмки.

Построение правильного 17-угольника было непосредственно осуществлено самим Гауссом, но впервые опубликовано К. Ф. фон Пфейдерером в 1802 г.
Правильный 257-угольник построил Ф. Ю. Ришело в 1832 г.
В библиотеке Гёттингенского университета хранится рукопись, являющаяся итогом 10-летней работы О. Гермеса, которая содержит метод построения правильного 65537-угольника.

	Один слишком навязчивый аспирант довёл своего руководителя до того, что тот сказал ему: «Идите и разработайте построение правильного многоугольника с 65537 сторонами». Аспирант удалился, чтобы вернуться через 20 лет с соответствующим построением.[1]

Ссылки

↑ Дж. Литлвуд Математическая смесь. — М.: Наука, 1990. — ISBN 5-02-014332-4

Правильные многоугольники
Основные	Треугольник • Квадрат • Пятиугольник • Шестиугольник • Семиугольник • Восьмиугольник • Девятиугольник • Семнадцатиугольник • 257-угольник • 65537-угольник
См. также	Многоугольник • Теорема Гаусса — Ванцеля

Wikimedia Foundation.2010.

Полезное

Смотреть что такое "Теорема Гаусса — Ванцеля" в других словарях:

Теорема Гаусса (значения) — Существует несколько утверждений, называемых теоремой Гаусса: Теорема Гаусса (закон Гаусса) в электростатике и электродинамике и общая формулировка ее формальной части Теорема Гаусса Остроградского в векторном анализе. Теорема Гаусса Ванцеля о… … Википедия
Теорема Бойяи — Гервина — утверждает, что любые два равновеликих многоугольника равносоставлены. Более формально: Пусть P и Q суть два многоугольника с одинаковой площадью. Тогда их можно разрезать соответственно на многоугольники и , так что для любого … Википедия
Теорема Бойяи — Теорема Бойяи Гервина утверждает, что любые два равновеликих многоугольника равносоставлены. Более формально: Пусть и суть два многоугольника с одинаковой площадью. Тогда их можно разрезать соответственно на многоугольники и , так что для… … Википедия
Теорема Брахмагупты — … Википедия
Проблема правильных многоугольников — Теорема Гаусса Ванцеля утверждает, что правильный n угольник возможно построить с помощью циркуля и линейки тогда и только тогда, когда , где различные простые числа Ферма. Это условие также эквивалентно тому, что значение функции Эйлера является … Википедия
Правильный 65537-угольник — 65537 угольник или окружность? Правильный 65537 угольник (шестѝдесятипятиты̀сячпятисо̀ттридцатисемиугольник) геометрическая фигура из группы правильных многоугольников, состоящая из 65537 … Википедия
Правильный семиугольник — Правильный семиугольник это правильный многоугольник с семью сторонами. Содержание … Википедия
Правильный 257-угольник — 257 угольник или окружность? Правильный 257 угольник правильный многоугольник с 257 сторонами. Содержание … Википедия
Гаусс, Карл Фридрих — У этого термина существуют и другие значения, см. Гаусс. Карл Фридрих Гаусс Carl Friedrich Gauß … Википедия
Правильный многоугольник — Правильный семиугольник Правильный многоугольник это выпуклый многоугольник, у которого все стороны и углы равны . Определение правильного многоугольника может зависеть от определения … Википедия