Многочлен Чебышева | это... Что такое Многочлен Чебышева? (original) (raw)

Многочлен Чебышева

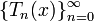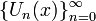Многочле́ны Чебышёва — две последовательности многочленов $\{ T_n(x)\}_{n=0}^{\infty}$ и $\{ U_n(x)\}_{n=0}^{\infty}$ , названные в честь их первооткрывателя Пафнутия Львовича Чебышёва.

T1, T2, T3, T4, T5

Многочлен Чебышёва первого рода T n(x) характеризуется как многочлен степени n со старшим коэффициентом 2_n_ - 1, который меньше всего отклоняется от нуля на интервале [ − 1,1].

U1, U2, U3, U4, U5

Многочлен Чебышёва второго рода U n(x) характеризуется как многочлен степени n со старшим коэффициентом 2_n_, интеграл от абсолютной величины которого по интервалу [ − 1,1] принимает наименьшее возможное значение.

Рекурсивное определение

Многочлены Чебышёва первого рода T n(x) могут быть определены с помощью рекуррентного соотношения:

$T_0(x) = 1 \,$

$T_1(x) = x \,$

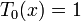
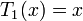
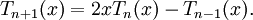
$T_{n+1}(x) = 2xT_n(x) - T_{n-1}(x). \,$

Многочлены Чебышёва второго рода U n(x) могут быть определены с помощью рекуррентного соотношения:

$U_0(x) = 1 \,$

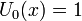
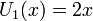
$U_1(x) = 2x \,$

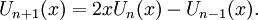
$U_{n+1}(x) = 2xU_n(x) - U_{n-1}(x). \,$

Явные формулы

Многочлены Чебышёва являются решениями уравнения Пелля:

T n(x)2 − (_x_2 − 1)U n − 1(x)2 = 1

в кольце многочленов с вещественными коэффициентами и удовлетворяют тождеству:

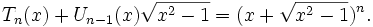
$T_n(x) + U_{n-1}(x)\sqrt{x^2-1} = (x + \sqrt{x^2-1})^n.$

Из последнего тождества также следуют явные формулы:

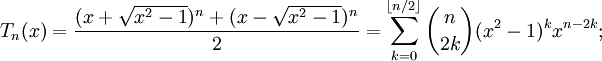
$T_n(x)=\frac{(x+\sqrt{x^2-1})^n+(x-\sqrt{x^2-1})^n}{2} = \sum_{k=0}^{\lfloor n/2\rfloor} \binom{n}{2k} (x^2-1)^k x^{n-2k};$

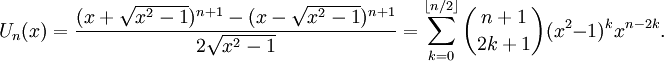
$U_n(x)=\frac{(x+\sqrt{x^2-1})^{n+1}-(x-\sqrt{x^2-1})^{n+1}}{2\sqrt{x^2-1}} = \sum_{k=0}^{\lfloor n/2\rfloor} \binom{n+1}{2k+1} (x^2-1)^k x^{n-2k}.$

Тригонометрическое определение

Многочлены Чебышёва первого рода T n(x) могут быть также определены с помощью равенства:

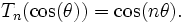
$T_n(\cos(\theta))=\cos(n\theta). \,$

или, что почти эквивалентно,

T n(z) = cos(n_arccos_z)

Многочлены Чебышёва второго рода U n(x) могут быть также определены с помощью равенства:

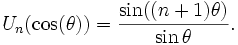
$U_n(\cos(\theta)) = \frac{\sin((n+1)\theta)}{\sin\theta}.$

Примеры

Несколько первых многочленов Чебышёва первого рода

$T_0(x) = 1 \,$

$T_1(x) = x \,$

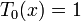
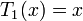
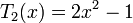
$T_2(x) = 2x^2 - 1 \,$

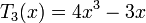
$T_3(x) = 4x^3 - 3x \,$

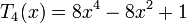
$T_4(x) = 8x^4 - 8x^2 + 1 \,$

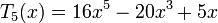
$T_5(x) = 16x^5 - 20x^3 + 5x \,$

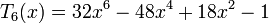
$T_6(x) = 32x^6 - 48x^4 + 18x^2 - 1 \,$

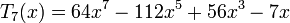
$T_7(x) = 64x^7 - 112x^5 + 56x^3 - 7x \,$

Несколько первых многочленов Чебышёва второго рода

$U_0(x) = 1 \,$

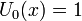
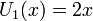
$U_1(x) = 2x \,$

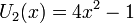
$U_2(x) = 4x^2 - 1 \,$

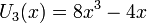
$U_3(x) = 8x^3 - 4x \,$

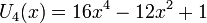
$U_4(x) = 16x^4 - 12x^2 + 1 \,$

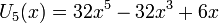
$U_5(x) = 32x^5 - 32x^3 + 6x \,$

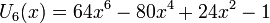
$U_6(x) = 64x^6 - 80x^4 + 24x^2 - 1 \,$

Свойства

Многочлены Чебышёва обладают следующими свойствами:

Обобщения

Вопрос о многочленах минимальной нормы с фиксированными коэффициентами при двух старших степенях был рассмотрен позднее Золотарёвым, найденные им полиномы носят название многочлены Золотарёва.

См. также

многочлены Фабера

Ссылки

Васильев Н., Зелевинский А., Многочлены Чебышёва и рекуррентные соотношения, Квант, № 1, 1982.

Wikimedia Foundation.2010.

Полезное

Смотреть что такое "Многочлен Чебышева" в других словарях:

Чебышева многочлены — специальная система многочленов, ортогональных с весом [ 1; 1] (см. Ортогональная система функций). Введены в 1854 П. Л. Чебышевым. * * * ЧЕБЫШЕВА МНОГОЧЛЕНЫ ЧЕБЫШЕВА МНОГОЧЛЕНЫ, специальная система многочленов, ортогональных с весом (Чебышева… … Энциклопедический словарь
ЧЕБЫШЕВА МНОГОЧЛЕНЫ — специальная система многочленов, ортогональных с весом (Чебышева многочлен 1 го рода) или с весом (Чебышева многочлен 2 го рода) на отрезке ЧЕБЫШЕВА ПАРАЛЛЕЛОГРАММ плоский 4 звенный шарнирный механизм для воспроизведения движения некоторой точки… … Большой Энциклопедический словарь
ЧЕБЫШЕВА ПОСТОЯННАЯ — числовая характеристика компактного множества Ена комплексной плоскости, употребляемая в теории наилучшего приближения. Пусть К п класс всех многочленов вида степени п, и пусть Существует многочлен для к poro М(tn)= т n, он наз. многочленом… … Математическая энциклопедия
ЧЕБЫШЕВА МНОГОЧЛЕНЫ — первого рода многочлены, ортогональные на отрезке [ 1, 1] с весовой функцией Для стандартизованных Ч. м. справедливы формула и рекуррентное соотношение с помощью к рых находят последовательно T0 (x) = 1, T1(x) = x, Т2 (х)=2х 2 1, T3(x) = 4x3 З х … Математическая энциклопедия
Чебышева многочлены — Многочлены Чебышёва две последовательности многочленов и , названные в честь их первооткрывателя Пафнутия Львовича Чебышёва. T1, T2, T3, T4 … Википедия
ЧЕБЫШЕВА УРАВНЕНИЕ — линейное однородное обыкновенное дифференциальное уравнение 2 го порядка или, в самосопряженной форме, здесь а константа. Ч. у. представляет собой частный случай гипергеометрического уравнения. Точки х= 1 и х=1 являются регулярными особыми… … Математическая энциклопедия
Многочлены Чебышева — Многочлены Чебышева две последовательности ортогональных многочленов и , названные в честь Пафнутия Львовича Чебышева. Многочлены Чебышева играют важную роль в теории приближений, поскольку корни многочленов Чебышева первого рода… … Википедия
Фильтр Чебышева — Линейные электронные фильтры Фильтр Баттерворта Фильтр Чебышева Эллиптический фильтр Фильтр Бесселя Фильтр Гаусса Фильтр Лежандра Фильтр Габора … Википедия
АЛГЕБРАИЧЕСКИЙ МНОГОЧЛЕН НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ — многочлен, наименее уклоняющийся от заданной функции. Точнее, пусть измеримая функция f(x).интегрируема с р й степенью на множество алгебраич. многочленов степени не выше п. Величину наз. наилучшим приближением, а многочлен, для к рого нижняя… … Математическая энциклопедия
НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ МНОГОЧЛЕН — наилучшего приближения полином, многочлен, осуществляющий наилучшее приближение функции в той или иной метрике среди всех многочленов, построенных по той же (конечной) системе функций. Если X линейное нормированное пространство функций (напр.,… … Математическая энциклопедия