Теорема Больцано — Вейерштрасса | это... Что такое Теорема Больцано — Вейерштрасса? (original) (raw)

Теорема Больцано — Вейерштрасса, или лемма Больцано — Вейерштрасса о предельной точке — предложение анализа, одна из формулировок которого гласит: из всякой ограниченной последовательности точек пространства $\mathbb{R}^n$ можно выделить сходящуюся подпоследовательность. Теорема Больцано — Вейерштрасса, в особенности случай числовой последовательности (n = 1), входит в каждый курс анализа. Она используется при доказательстве многих предложений анализа, например, теоремы о достижении непрерывной на отрезке функцией своих точных верхней и нижней граней. Теорема носит имена чешского математика Больцано и немецкого математика Вейерштрасса, которые независимо друг от друга ее сформулировали и доказали.

Содержание

1 Формулировки
2 Доказательство
- 2.1 Одномерный случай
- 2.2 Распространение на случай пространства произвольной размерности
3 История
4 Теорема Больцано — Вейерштрасса и понятие компактности
5 См. также
6 Примечания
7 Литература

Формулировки

Известно несколько формулировок теоремы Больцано — Вейерштрасса.

Первая формулировка

Пусть предложена последовательность точек пространства $\mathbb{R}^n$ :

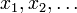
$x_1, x_2, \ldots$

и пусть эта последовательность ограничена, то есть

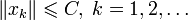
$\| x_k \| \leqslant C, \; k = 1, 2, \ldots$

где C > 0 — некоторое число.

Тогда из данной последовательности можно выделить подпоследовательность

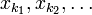
$x_{k_1}, x_{k_2}, \ldots$

которая сходится к некоторой точке пространства $\mathbb{R}^n$ .

Теорему Больцано — Вейерштрасса в такой формулировке иногда называют принципом компактности ограниченной последовательности.

Расширенный вариант первой формулировки

Нередко теорему Больцано — Вейерштрасса дополняют следующим предложением.

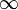Если последовательность точек пространства $\mathbb{R}^n$ неограничена, то из нее можно выделить последовательность, имеющую пределом $\infty$ .

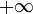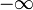Для случая n = 1 эту формулировку можно уточнить: из любой неограниченной числовой последовательности можно выделить подпоследовательность, имеющую пределом бесконечность определенного знака ( $+\infty$ или $-\infty$ ).

Таким образом, всякая числовая последовательность содержит подпоследовательность, имеющую предел в расширенном множестве действительных чисел 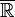$\overline{\mathbb{R}}$ .

Вторая формулировка

Следующее предложение является альтернативной формулировкой теоремы Больцано — Вейерштрасса.

Всякое ограниченное бесконечное подмножество E пространства $\mathbb{R}^n$ имеет по крайней мере одну предельную точку в $\mathbb{R}^n$ .

Более подробно, это означает, что существует точка 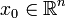$x_0 \in \mathbb{R}^n$ , всякая окрестность 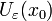$U_{\varepsilon}(x_0)$ которой содержит бесконечное число точек множества E.

Доказательство эквивалентности двух формулировок теоремы Больцано — Вейерштрасса

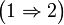$\bigl ( 1 \Rightarrow 2 \bigr )$ Пусть E — ограниченное бесконечное подмножество пространства $\mathbb{R}^n$ . Возьмем в E последовательность различных точек

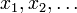
$x_1, x_2, \ldots$

Поскольку эта последовательность ограничена, в силу первой формулировки теоремы Больцано — Вейерштрасса из нее можно выделить подпоследовательность

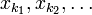
$x_{k_1}, x_{k_2}, \ldots$

сходящуюся к некоторой точке 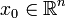$x_0 \in \mathbb{R}^n$ . Тогда всякая окрестность точки _x_0 содержит бесконечное число точек множества E.

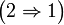$\bigl ( 2 \Rightarrow 1 \bigr )$ Обратно, пусть дана произвольная ограниченная последовательность точек пространства $\mathbb{R}^n$ :

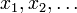$x_1, x_2, \ldots$ Множество значений E данной последовательности ограничено, но может быть как бесконечным, так и конечным. Если E конечно, то одно из значений 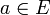$a \in E$ повторяется в последовательности бесконечное число раз. Тогда эти члены образуют стационарную подпоследовательность, сходящуюся к точке a.

Если же множество E бесконечно, то в силу второй формулировки теоремы Больцано — Вейерштрасса, существует точка 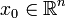$x_0 \in \mathbb{R}^n$ , в любой окрестности которой имеется бесконечное много различных членов последовательности.

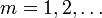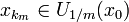Выберем последовательно для $m = 1, 2, \ldots$ точки $x_{k_m} \in U_{1/m}(x_0)$ , соблюдая при этом условие возрастания номеров:

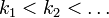
$k_1 < k_2 < \ldots$

Тогда подпоследовательность 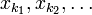$x_{k_1}, x_{k_2}, \ldots$ сходится к точке _x_0.

Доказательство

Теорема Больцано — Вейерштрасса выводится из свойства полноты множества действительных чисел. В наиболее известном варианте доказательства используется свойство полноты в форме принципа вложенных отрезков.

Одномерный случай

Докажем, что из любой ограниченной числовой последовательности можно выделить сходящуюся подпоследовательность. Нижеизложенный способ доказательства называется методом Больцано, или методом деления пополам.

Пусть дана ограниченная числовая последовательность

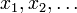
$x_1, x_2, \ldots$

Из ограниченности последовательности следует, что все ее члены лежат на некотором отрезке числовой прямой, который обозначим [_a_0,_b_0].

Разделим отрезок [_a_0,_b_0] пополам на два равных отрезка. По крайней мере один из получившихся отрезков содержит бесконечное число членов последовательности. Обозначим его [_a_1,_b_1].

На следующем шаге повторим процедуру с отрезком [_a_1,_b_1]: разделим его на два равных отрезка и выберем из них тот, на котором лежит бесконечное число членов последовательности. Обозначим его [_a_2,_b_2].

Продолжая процесс получим последовательность вложенных отрезков

$[a_0, b_0] \supset [a_1, b_1] \supset [a_2, b_2] \supset \ldots$

в которой каждый последующий является половиной предыдущего, и содержит бесконечное число членов последовательности {x k}.

Длины отрезков стремятся к нулю:

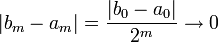
$|b_m - a_m| = \frac{|b_0 - a_0|}{2^m} \to 0$

В силу принципа вложенных отрезков Коши — Кантора, существует единственная точка ξ, принадлежащая всем отрезкам:

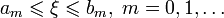
$a_m \leqslant \xi \leqslant b_m, \; m = 0, 1, \ldots$

По построению на каждом отрезке [a m,b _m_] лежит бесконечное число членов последовательности. Выберем последовательно

$x_{k_m} \in [a_m,b_m], \; m = 0, 1, 2, \ldots$

соблюдая при этом условие возрастания номеров:

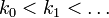
$k_0 < k_1 < \ldots$

Тогда подпоследовательность 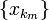$\{ x_{k_m} \}$ сходится к точке ξ. Это следует из того, что расстояние от 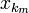$x_{k_m}$ до ξ не превосходит длины содержащего их отрезка [a m,b _m_], откуда

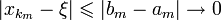
$|x_{k_m} - \xi | \leqslant |b_m - a_m| \to 0$

Распространение на случай пространства произвольной размерности

Теорема Больцано — Вейерштрасса легко обобщается на случай пространства произвольной размерности.

Пусть дана последовательность точек пространства $\mathbb{R}^n$ :

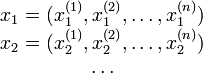
$\begin{matrix} x_1 = (x_1^{(1)}, x_1^{(2)}, \ldots, x_1^{(n)}) \\ x_2 = (x_2^{(1)}, x_2^{(2)}, \ldots, x_2^{(n)}) \\ \ldots \\ \end{matrix}$

(нижний индекс — номер члена последовательности, верхний — номер координаты). Если последовательность точек пространства $\mathbb{R}^n$ ограничена, то каждая из числовых последовательностей координат:

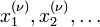
$x_1^{(\nu)}, x_2^{(\nu)}, \ldots$

также ограничена (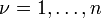 $\nu = 1, \ldots, n$ — номер координаты).

В силу одномерного варианта теоремы Больцано — Вейрштрасса из последовательности {x k} можно выделить подпоследовательность точек 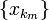$\{ x_{k_m} \}$ , первые координаты которых 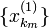$\{ x_{k_m}^{(1)} \}$ образуют сходяющуюся последовательность. Из полученной подпоследовательности еще раз выделим подпоследовательность, сходящуюся по второй координате. При этом сходимость по первой координате сохранится в силу того, что всякая подпоследовательность сходящейся последовательности также сходится. И так далее.

После n шагов получим некоторую последовательность

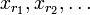
$x_{r_1}, x_{r_2}, \ldots$

являющуюся подпоследовательностью 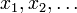$x_1, x_2, \ldots$ , и сходящуюся по каждой из координат. Отсюда следует, что эта подпоследовательность сходится.

История

Теорема Больцано — Вейерштрасса (для случая n = 1) впервые была доказана чешским математиком Больцано в 1817 году. В работе Больцано она выступала как лемма в доказательстве теоремы о промежуточных значениях непрерывной функции, известной теперь как теорема Больцано — Коши. Однако эти и другие результаты, доказанные Больцано задолго до Коши и Вейерштрасса, остались незамеченными.

Лишь через полвека Вейерштрасс, независимо от Больцано, заново открыл и доказал эту теорему. Первоначально называлась теоремой Вейерштрасса, до того как стали известны и получили признание работы Больцано.

Сегодня эта теорема носит имена Больцано и Вейерштрасса. Нередко эту теорему называют леммой Больцано — Вейерштрасса, а иногда леммой о предельной точке.

Теорема Больцано — Вейерштрасса и понятие компактности

Теорема Больцано — Вейерштрасса устанавливает следующее интересное свойство ограниченного множества 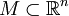$M \subset \mathbb{R}^n$ : всякая последовательность точек M содержит сходящуюся подпоследовательность.

При доказательстве различных предложений в анализе часто прибегают к следующему приему: определяют последовательность точек, обладающую каким-либо нужным свойством, а затем из нее выделяют подпоследовательность, также им обладающую, но уже сходящуюся. Например, именно так доказывается теорема Вейерштрасса о том, что непрерывная на отрезке функция ограничена и принимает свои наибольшее и наименьшее значения.

Эффективность подобного приема вообще, а также желание распространить теорему Вейерштрасса на произвольные метрические пространства, побудили в 1906 году французского математика Мориса Фреше ввести понятие компактности. Свойство ограниченных множеств в $\mathbb{R}^n$ , устанавливаемое теоремой Больцано—Вейерштрасса, заключается, образно говоря, в том, что точки множества располагаются достаточно «тесно», или же «компактно»: сделав бесконечное число шагов по этому множеству, мы непременно сколь угодно близко подойдем к какой-то точке пространства.

Фреше вводит следующее определение: множество M называется компактным, или же компактом, если всякая последовательность его точек содержит подпоследовательность, сходящуюся к некоторой точке этого множества. При этом предполагается, что на множестве M определена метрика, то есть оно является метрическим пространством, либо подмножеством метрического пространства.

Если исходить из этого определения, то не всякое ограниченное множество 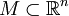$M \subset \mathbb{R}^n$ является компактным: подпоследовательность точек из M может сходится к точке, уже не принадлежащей этому множеству. Однако замыкание ограниченного множества уже будет компактом. 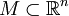Тем самым теорема Больцано — Вейерштрасса устаналивает достаточное условие компактности в пространстве $\mathbb{R}^n$ : для того чтобы множество $M \subset \mathbb{R}^n$ было компактным достаточно, чтобы оно было замкнутым и ограниченным. Нетрудно убедится в необходимости этих условий (это намного проще, чем доказать достаточность).

Таким образом, с точки зрения общего определения компактности роль теоремы Больцано — Вейерштрасса заключается в том, что она устанавливает критерий компактности в пространстве $\mathbb{R}^n$ : компакты в $\mathbb{R}^n$ — в точности замкнутые ограниченные множества.

См. также

Примечания

Литература

Кудрявцев Л. Д. Курс математического анализа. — 5-е изд. — М.: «Дрофа», 2003. — Т. 1. — 704 с. — ISBN 5-7107-4119-1
Рыбников К. А. История математики. — М.: Издательство Московского университета, 1963. — Т. 2.
Рудин У. Основы математического анализа = Principles of Mathematical Analysis / пер. с англ. Хавина. — второе, стереотипное. — М.: «Мир», 1976.