Противоречивость теории | это... Что такое Противоречивость теории? (original) (raw)

Содержание

• 1 Определение и разновидности
• 2 Разновидности дедуктивных теорий
  • 2.1 Задание аксиом и правил вывода
    * 2.1.1 Примеры
  • 2.2 Задание только аксиом
    * 2.2.1 Примеры
  • 2.3 Задание только правил вывода
    * 2.3.1 Примеры
• 3 Свойства дедуктивных теорий
  • 3.1 Противоречивость
  • 3.2 Полнота
  • 3.3 Независимость аксиом
  • 3.4 Разрешимость
• 4 Примеры
• 5 Важнейшие выводы
• 6 Литература
• 7 Примечания
• 8 См. также

Определение и разновидности

Дедуктивная теория считается заданной, если:

1. Задан алфавит (множество) и правила образования выражений (слов) в этом алфавите.
2. Заданы правила образования формул (правильно построенных, корректных выражений).
3. Из множества формул некоторым способом выделено подмножество T теорем (доказуемых формул).

Разновидности дедуктивных теорий

В зависимости от способа построения множества теорем:

Задание аксиом и правил вывода

В множестве формул выделяется подмножество аксиом, и задается конечное число правил вывода — таких правил, с помощью которых (и только с помощью их) из аксиом и ранее выведенных теорем можно образовать новые теоремы. Все аксиомы также входят в число теорем. Иногда (например в аксиоматике Пеано) теория содержит бесконечное количество аксиом, задающихся при помощи одной или нескольких схем аксиом. Аксиомы иногда называют «скрытыми определениями».

Примеры

Таким способом задается формальная теория (формальная аксиоматическая теория, формальное (логическое) исчисление).

Задание только аксиом

Задаются только аксиомы, правила вывода считаются общеизвестными.

При таком задании теорем говорят, что задана полуформальная аксиоматическая теория.

Примеры

Геометрия

Задание только правил вывода

Аксиом нет (множество аксиом пусто), задаются только правила вывода.

По сути, заданная таким образом теория — частный случай формальной, но имеет собственное название: теория естественного вывода.

Примеры

Свойства дедуктивных теорий

Противоречивость

Теория, в которой множество теорем покрывает всё множество формул (все формулы являются теоремами, «истинными высказываниями»), называется противоречивой. В противном случае теория называется непротиворечивой. Выяснение противоречивости теории — одна из важнейших и иногда сложнейших задач формальной логики. После выяснения противоречивости теория, как правило, не имеет дальнейшего ни теоретического, ни практического применения.

Полнота

Теория называется полной, если в ней для любой формулы F выводима либо сама F, либо ее отрицание 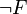. В противном случае, теория содержит недоказуемые утверждения (утверждения, которые нельзя ни доказать, ни опровергнуть средствами самой теории), и называется неполной.

Независимость аксиом

Отдельная аксиома теории считается независимой, если эту аксиому нельзя вывести из остальных аксиом. Зависимая аксиома по сути избыточна, и ее удаление из системы аксиом никак не отразится на теории. Вся система аксиом теории называется независимой, если каждая аксиома в ней независима.

Разрешимость

Теория называется разрешимой, если в ней понятие теоремы эффективно, то есть существует эффективный процесс (алгоритм), позволяющий для любой формулы за конечное число шагов определить, является она теоремой или нет.

Примеры

• Исчисление высказываний (логика высказываний, теория L)
• Теория первого порядка (теория K), и частный случай — логика первого порядка (исчисление предикатов, теория K1)
• Формальная арифметика (теория S)

Важнейшие выводы

• В 30-е гг. XX века Курт Гёдель показал, что есть целый класс теорий первого порядка, являющихся неполными. Более того, формула, утверждающая непротиворечивость теории, также невыводима средствами самой теории (см. Теоремы Гёделя о неполноте). Этот вывод имел огромное значение для математики, так как формальная арифметика (а на ней базируется теория действительных чисел, без которой нельзя представить современную математику) является как раз такой теорией первого порядка, а следовательно, формальная арифметика и все теории, содержащие ее, в том числе теория действительных чисел, являются неполными.
• Проблема неразрешимости логики предикатов. Чёрчем доказано, что не существует алгоритма, который для любой формулы логики предикатов устанавливает, логически общезначима формула или нет.
• Исчисление высказываний является непротиворечивой, полной, разрешимой теорией, причем все три утверждения доказуемы в рамках самой логики высказываний.

Литература

• Галиев Ш. И. Математическая логика и теория алгоритмов. — Казань: Издательство КГТУ им. А. Н. Туполева. 2002.

Примечания

См. также

• Аксиома выбора
• Теория множеств

Wikimedia Foundation.2010.