Фактор Лоренца | это... Что такое Фактор Лоренца? (original) (raw)

Фактор Лоренца

Быстрота́ (англ. rapidity) — в релятивистской кинематике монотонно возрастающая функция скорости, которая стремится к бесконечности, когда скорость стремится к скорости света. В отличие от скорости, для которой закон сложения нетривиален, для быстроты характерен простой закон сложения («быстрота аддитивна»).

Быстрота выражается формулой:

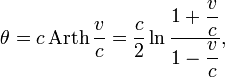
$\theta=c\,\mathrm{Arth}\,\frac{v}{c}=\frac{c}{2}\ln\frac{1+\dfrac{v}{c}}{1-\dfrac{v}{c}},$

где

θ — быстрота,
v — обычная скорость,
c — скорость света,
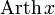$\mathrm{Arth}\,x$ — ареатангенс.

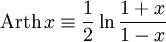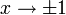
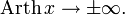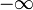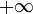Ареатангенс (или гиперболический арктангенс) $\mathrm{Arth}\,x\equiv\frac{1}{2}\ln\frac{1+x}{1-x}$ определён в области значений аргумента от −1 до +1; при $x\to\plusmn 1$ $\mathrm{Arth}\,x\to\plusmn\infty.$ Таким образом, быстрота имеет размерность скорости и при изменении скорости от − c до + c меняется от $-\infty$ до $+\infty$ . Иногда вводят также параметр быстроты 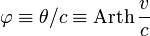$\varphi\equiv\theta/c\equiv\mathrm{Arth}\,\frac{v}{c}$ — безразмерную величину, которую иногда также называют быстротой.

В пределе малых скоростей быстрота примерно равна скорости:

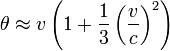$\theta\approx v\left(1+\frac{1}{3}\left(\frac{v}{c}\right)^2\right)$ при $v\ll c.$ .

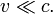Связанная с быстротой часто используемая величина — фа́ктор Ло́ренца, или Ло́ренц-фа́ктор, названный по имени Г. А. Лоренца и определяемый как

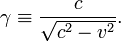
$\gamma\equiv\frac{c}{\sqrt{c^2-v^2}}.$

Лоренц-фактор равен гиперболическому косинусу параметра быстроты:

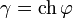$\gamma=\mathrm{ch}\,\varphi$ .

С увеличением скорости от 0 до c Лоренц-фактор γ увеличивается от 1 до 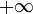$+\infty$ .

Аддитивность быстроты

Пусть в некоторой инерциальной системе отсчёта K две частицы движутся вдоль одной прямой, скорость одной из них равна _v_1, а скорость второй относительно первой равна v'2 (скорости могут быть как положительными, так и отрицательными). Обозначим скорость второй частицы в системе K через _v_2. При малых (по сравнению со скоростью света c) скоростях приближённо выполняется галилеевский закон сложения скоростей _v_2 = _v_1 + v'2. Однако в релятивистском случае эта формула не действует, и скорость второй частицы необходимо вычислять с помощью лоренцевых преобразований. Релятивистский закон сложения скоростей

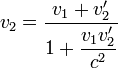
$v_2=\frac{v_1+v'_2}{1+\dfrac{v_1v'_2}{c^2}}$

отличается от галилеевского знаменателем, который при малых скоростях близок к единице. Рассмотрим соответствующие скоростям быстроты 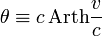$\theta \equiv c\,\mathrm{Arth}\frac{v}{c}$ . Оказывается, что быстрота второй частицы в системе отсчёта K равна сумме быстрот:

θ2 = θ1 + θ'2.

Удобство записи закона сложения скоростей в терминах быстрот привело к тому, что эта величина довольно широко используется в релятивистской кинематике, особенно в ускорительной физике. Однако следует помнить, что сложение быстрот совпадает по виду с галилеевским векторным сложением скоростей только при одномерном движении частиц.

См. также

Псевдобыстрота
Лоренцевский буст

Литература

Бабурова О. В. Релятивистская кинематика и геометрия Лобачевского // Соросовский образовательный журнал. — т. 8. — 2004. — с. 77—84 [1].
Прохоров А. М., Физическая энциклопедия. — М.: Советская энциклопедия, 1988. — Т. 1. — С. 233. — 704 с.

Wikimedia Foundation.2010.

Полезное

Смотреть что такое "Фактор Лоренца" в других словарях:

Лоренца преобразования — Преобразованиями Лоренца в физике, в частности в специальной теории относительности (СТО), называются преобразования, которым подвергаются пространственно временные координаты (x,y,z,t) каждого события при переходе от одной инерциальной системы… … Википедия
Преобразование Лоренца — Преобразованиями Лоренца в физике, в частности в специальной теории относительности (СТО), называются преобразования, которым подвергаются пространственно временные координаты (x,y,z,t) каждого события при переходе от одной инерциальной системы… … Википедия
Вывод преобразований Лоренца — может быть проделан многими способами, исходя из различных предпосылок. Преобразования Лоренца могут быть получены абстрактно, из групповых соображений (в этом случае они получаются с неопределённым ), как обобщение преобразований Галилея (что… … Википедия
Преобразования Лоренца — Преобразования Лоренца линейные (или аффинные) преобразования векторного (соответственно, аффинного) псевдоевклидова пространства, сохраняющее длины или, что эквивалентно, скалярное произведение векторов. Преобразования Лоренца… … Википедия
Лоренц-фактор — Фактор Лоренца, или лоренц фактор, гамма фактор безразмерная физическая величина, используемая в релятивистской кинематике, монотонно возрастающая положительная функция скорости. Названа по имени Г. А. Лоренца. Определяется как… … Википедия
Специальная теория относительности — Почтовая марка с формулой E = mc2, посвящённая Альберту Эйнштейну, одному из создателей СТО. Специальная теор … Википедия
Уравнения Максвелла — Классическая электродинамика … Википедия
Быстрота — (англ. rapidity) в релятивистской кинематике монотонно возрастающая функция скорости, которая стремится к бесконечности, когда скорость стремится к скорости света. В отличие от скорости, для которой закон сложения нетривиален, для… … Википедия
Список обозначений в физике — Необходимо проверить качество перевода и привести статью в соответствие со стилистическими правилами Википедии. Вы можете помочь … Википедия
Форма релятивистских объектов — Внешний вид объектов, двигающихся с релятивистской скоростью, существенно зависит от формы объекта и способа его наблюдения. Можно выделить два основных способа: одновременное фиксирование положения точек поверхности и фотографирование при помощи … Википедия