Сортировка с помощью двоичного дерева | это... Что такое Сортировка с помощью двоичного дерева? (original) (raw)

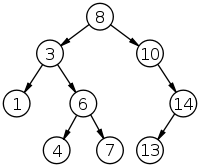
Пример двоичного дерева

Сортировка с помощью двоичного дерева (сортировка двоичным деревом, сортировка деревом, древесная сортировка, сортировка с помощью бинарного дерева, англ. tree sort) — универсальный алгоритм сортировки, заключающийся в построении двоичного дерева поиска по ключам массива (списка), с последующей сборкой результирующего массива путём обхода узлов построенного дерева в необходимом порядке следования ключей. Данная сортировка является оптимальной при получении данных путём непосредственного чтения с потока (например с файла, сокета или консоли).

Алгоритм

1. Построение двоичного дерева.

2. Сборка результирующего массива путём обхода узлов в необходимом порядке следования ключей.

Эффективность

Процедура добавления объекта в бинарное дерево имеет среднюю алгоритмическую сложность порядка O(log(n)). Соответственно, для n объектов сложность будет составлять O(n log(n)), что относит сортировку с помощью двоичного дерева к группе «быстрых сортировок». Однако, сложность добавления объекта в разбалансированное дерево может достигать O(n), что может привести к общей сложности порядка O(n²).

При физическом развёртывании древовидной структуры в памяти требуется не менее чем 4n ячеек дополнительной памяти (каждый узел должен содержать ссылки на элемент исходного массива, на родительский элемент, на левый и правый лист), однако, существуют способы уменьшить требуемую дополнительную память.

Примеры реализации

В простой форме функционального программирования на Haskell данный алгоритм будет выглядеть так:

data Tree a = Leaf | Node (Tree a) a (Tree a)

insert :: Ord a => a -> Tree a -> Tree a insert x Leaf = Node Leaf x Leaf insert x (Node t y t') | x <= y = Node (insert x t) y t' insert x (Node t y t') | x > y = Node t y (insert x t')

flatten :: Tree a -> [a] flatten Leaf = [] flatten (Node t x t') = flatten t ++ [x] ++ flatten t'

treesort :: Ord a => [a] -> [a] treesort = flatten . foldr insert Leaf

Реализация на C++:

#include
#include #include

template void binary_tree_sort(Iterator begin, Iterator end) { std::multiset<typename std::iterator_traits::value_type> tree(begin, end); std::copy(tree.begin(), tree.end(), begin); };

Пример создания бинарного дерева и сортировки на языке Java:

// Скомпилируйте и введите java TreeSort class Tree { public Tree left; // левое и правое поддеревья и ключ public Tree right; public int key;

public Tree(int k) { // конструктор с инициализацией ключа key = k; }

/* insert (добавление нового поддерева (ключа)) сравнить ключ добавляемого поддерева (К) с ключом корневого узла (X). Если K>=X, рекурсивно добавить новое дерево в правое поддерево. Если K<X, рекурсивно добавить новое дерево в левое поддерево. Если поддерева нет, то вставить на это место новое дерево */ public void insert( Tree aTree) { if ( aTree.key < key ) if ( left != null ) left.insert( aTree ); else left = aTree; else if ( right != null ) right.insert( aTree ); else right = aTree; }

/* traverse (обход) Рекурсивно обойти левое поддерево. Применить функцию f (печать) к корневому узлу. Рекурсивно обойти правое поддерево. */ public void traverse(TreeVisitor visitor) { if ( left != null) left.traverse( visitor );

  visitor.visit(this);

  if ( right != null ) 
        right.traverse( visitor );

} }

interface TreeVisitor { public void visit(Tree node); };

class KeyPrinter implements TreeVisitor { public void visit(Tree node) { System.out.println( " " + node.key ); } };

public class TreeSort { public static void main(String args[]) { Tree myTree; myTree = new Tree( 7 ); // создать дерево (с ключом) myTree.insert( new Tree( 5 ) ); // присоединять поддеревья myTree.insert( new Tree( 9 ) ); myTree.traverse(new KeyPrinter()); } }

См. также

• Двоичное дерево поиска

Алгоритмы сортировки
Теория	Сложность • О-нотация • Отношение порядка • Типы сортировки: Устойчивая • Внутренняя • Внешняя
Алгоритмы	Обменные: Пузырьком • Перемешиванием • Гномья • Быстрая • Расчёской • Выбором: Выбором • Пирамидальная • Вставками: Вставками • Шелла • Деревом • Слиянием: Слиянием • Без дополнительной памяти • Без сравнений: Подсчётом • Поразрядная • Блочная • Гибридные: Introsort • Timsort • Прочее: Топологическая • Сети • Непрактичные: Bogosort • Stooge sort • Глупая • Блинная