Статистика Бозе — Эйнштейна | это... Что такое Статистика Бозе — Эйнштейна? (original) (raw)

Статистика Бозе — Эйнштейна

Статистическая физика
$S = k_B \, \ln\Omega$
Термодинамика Молекулярно-кинетическая теория Статистики Максвелла-Больцмана Бозе-Эйнштейна · Ферми-ДиракаParastatistics · Anyonic statisticsBraid statistics Ансамбли Микроканонический · Канонический Большой каноническийИзотермо-изобарическийИзоэнатльпи-изобарический Термодинамика Уравнение состояния · Цикл Карно · Закон Дюлонга — Пти Модели Модель Дебая · Эйнштейна · Модель Изинга Потенциалы Внутренняя энергия · Энтальпия Свободная энергия Гельмгольца потенциал Гиббса · Большой термодинамический потенциал Известные учёные Максвелл · Гиббс · Больцман

В статистической механике статистика Бо́зе — Эйнште́йна определяет распределение тождественных частиц с нулевым или целочисленным спином (таковыми являются, например, фотоны и атомы гелия-4) по энергетическим уровням в состоянии термодинамического равновесия. В 1920 году она была предложена Шатьендранатом Бозе для описания фотонов. В 1924 году Альберт Эйнштейн обобщил её на системы атомов с целым спином.

Описание

Статистикам Ферми — Дирака и Бозе — Эйнштейна подчиняются системы тождественных частиц, в которых нельзя пренебречь квантовыми эффектами. Квантовые эффекты проявляются при значениях концентрации частиц (N/V) ≥ n q, где n q — это т. н. квантовая концентрация, при которой среднее расстояние между частицами равно средней волне де Бройля для идеального газа при заданной температуре. При концентрации n q волновые функции частиц «касаются» друг друга, но практически не перекрываются. Статистике Ферми — Дирака подчиняются т. н. фермионы (частицы, для которых справедлив принцип запрета Паули), а статистике Бозе — Эйнштейна — бозоны. Поскольку квантовая концентрация растёт с увеличением температуры, большинство физических систем при высоких температурах подчиняется классической статистике Максвелла — Больцмана. Исключениями являются системы с очень высокой плотностью, например белые карлики. В пределе высокой температуры или низкой концентрации частиц обе статистики переходят в классическую статистику Максвелла — Больцмана.

Бозоны, в отличие от фермионов, не подчиняются принципу запрета Паули — произвольное количество частиц может одновременно находиться в одном состоянии. Из-за этого их поведение сильно отличается от поведения фермионов при низких температурах. В случае бозонов при понижении температуры все частицы будут собираться в одном состоянии, обладающем наименьшей энергией, формируя т. н. Бозе-конденсат.

Согласно статистике Бозе — Эйнштейна, количество частиц в заданном состоянии i, равняется

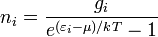
$n_i = \frac{g_i}{e^{(\varepsilon_i-\mu)/kT}-1}$

где 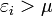$\varepsilon_i > \mu$ , ni — количество частиц в состоянии i, gi — вырождение уровня i, εi — энергия состояния i, μ — химпотенциал системы, k — постоянная Больцмана, T — абсолютное значение температуры.

В пределе 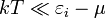$kT \ll \varepsilon_i-\mu$ статистика Бозе-Эйнштейна переходит в статистику Максвелла — Больцмана, а в пределе 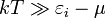$kT \gg \varepsilon_i-\mu$ — в распределение Рэлея — Джинса:

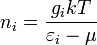$n_i = \frac{g_i kT}{\varepsilon_i-\mu}$ .

Литература

Статистика Бозе — Эйнштейна // Большая советская энциклопедия.

Cм. также

Wikimedia Foundation.2010.