Рациональная дробь | это... Что такое Рациональная дробь? (original) (raw)

Рациональная дробь

Рациональная дробь — это дробь, числителем и знаменателем которой являются многочлены. Она имеет вид

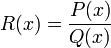
$R(x) = \frac{P(x)}{Q(x)}$

где P(x) и Q(x) некоторые многочлены.

Различают правильные и неправильные рациональные дроби, по аналогии с обычными числовыми дробями. Рациональная дробь называется правильной, если порядок знаменателя больше порядка числителя, и неправильной, если наоборот.

Любую неправильную рациональную дробь можно преобразовать в сумму некоторого многочлена и правильной рациональной дроби

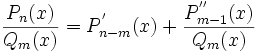
$\frac{P_n(x)}{Q_m(x)} = P^'_{n-m}(x) + \frac{P^{''}_{m-1}(x)}{Q_m(x)}$

Любую рациональную дробь многочленов с вещественными коэффициентами можно представить как сумму рациональных дробей, знаменателями которых являются выражения (x − a)k (a — вещественный корень Q(x)) либо (_x_2 + p x + q)k (где _x_2 + p x + q не имеет действительных корней), причём степени k не больше кратности соответствующих корней в многочлене Q(x). На основании этого утверждения основана теорема об интегрируемости рациональной дроби. Согласно ей, любая рациональная дробь может быть интегрирована в элементарных функциях, что делает класс рациональных дробей весьма важным в математическом анализе.

C этим связан метод выделения рациональной части в первообразной от рациональной дроби, который был предложен в 1844 году М. В. Остроградским.

См. также

Wikimedia Foundation.2010.

Полезное

Смотреть что такое "Рациональная дробь" в других словарях:

Рациональная функция — Рациональная функция это дробь, числителем и знаменателем которой являются многочлены. Она имеет вид где , многочлены от любого числа переменных. Частным случаем являются рациональные функции одного переменного: , где… … Википедия
Дробь (математика) — У этого термина существуют и другие значения, см. Дробь. 8 / 13 числитель числитель знаменатель знаменатель Две записи одной дроби Дробь в математике число, состоящее из одной или нескольких частей… … Википедия
Дробь — В Викисловаре есть статья «дробь» Наименование символа «⁄» (другое, распространённое по большей части в английском языке, название символа солидус (англ.), или слэш), например, в номерах домов. Так номер дома «5/17» читается «пять… … Википедия
РАЦИОНАЛЬНАЯ ФУНКЦИЯ — 1) Р. ф. функция w=R(z), где R(z) рациональное выражение от z, т. е. выражение, полученное из независимого переменного z и нек рого конечного набора чисел (действительных или комплексных) посредством конечного числа арифметич. действий. Р. ф.… … Математическая энциклопедия
Неправильная дробь — Четверти Рациональное число (лат. ratio отношение, деление, дробь) число, представляемое обыкновенной дробью , где m целое число, а n натуральное число. При этом число m называется числителем, а число n знаменателем дроби . Таку … Википедия
Обыкновенная дробь — Четверти Рациональное число (лат. ratio отношение, деление, дробь) число, представляемое обыкновенной дробью , где m целое число, а n натуральное число. При этом число m называется числителем, а число n знаменателем дроби . Таку … Википедия
Правильная дробь — Четверти Рациональное число (лат. ratio отношение, деление, дробь) число, представляемое обыкновенной дробью , где m целое число, а n натуральное число. При этом число m называется числителем, а число n знаменателем дроби . Таку … Википедия
Наипростейшая дробь — У этого термина существуют и другие значения, см. Дробь. Наипростейшей дробью ой степени называется рациональная функция вида где принимает натуральные значения, а точки , являющиеся полюсами функции , не обязательно геометрически различны.… … Википедия
РАЦИОНАЛЬНОЕ ЧИСЛО — число, выражаемое рациональной дробью. Формальная теория Р. ч. строится с помощью пар целых чисел. Р а ц и о н а л ь н о й д р о б ь ю наз. упорядоченная пара ( а, b )целых чисел а и b, у к рой b№0. Две рациональные дроби и наз. э к в и в а л е н … Математическая энциклопедия
Рациональные числа — Четверти Рациональное число (лат. ratio отношение, деление, дробь) число, представляемое обыкновенной дробью , где m целое число, а n натуральное число. При этом число m называется числителем, а число n знаменателем дроби . Таку … Википедия