Признак сходимости Д’Аламбера | это... Что такое Признак сходимости Д’Аламбера? (original) (raw)

Признак сходимости Д’Аламбера

Признак Д’Аламбера — признак сходимости числовых рядов, установлен Жаном Д’Аламбером в 1768 г.

Если для числового ряда

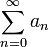
$\sum_{n=0}^\infty a_n$

существует такое число q, 0 < q < 1, что начиная с некоторого номера выполняется неравенство

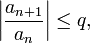
$\left| \frac {a_{n+1}} {a_{n}} \right| \le q,$

то данный ряд абсолютно сходится; если же, начиная с некоторого номера

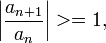
$\left| \frac {a_{n+1}} {a_{n}} \right| >= 1,$

то ряд расходится.

В частности, если существует предел

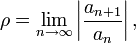
$\rho = \lim_{n \to \infty} \left| \frac {a_{n+1}} {a_n} \right|,$

то рассматриваемый ряд абсолютно сходится если ρ < 1, а если ρ > 1 — расходится (признак сходимости Д’Аламбера в предельной форме).

Примеры

Ряд

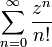
$\sum_{n=0}^\infty \frac {z^n} {n!}$

абсолютно сходится для всех комплексных z, так как

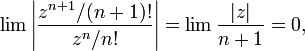
$\lim \left|\frac {{z^{n+1}}/{(n+1)!}} {{z^n}/{n!}}\right| = \lim \frac {|z|} {n+1} = 0,$

Ряд

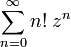
$\sum_{n=0}^\infty n! \; z^n$

расходится при всех 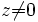$z\not=0$ , так как

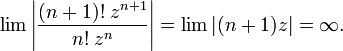
$\lim \left| \frac {(n+1)! \; z^{n+1}} {n! \; z^n} \right| = \lim |(n+1)z| = \infty.$

Если ρ = 1, то ряд может как сходиться, так и расходиться: оба ряда

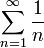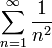
$\sum_{n=1}^\infty \frac 1 n$ и $\sum_{n=1}^\infty \frac 1 {n^2}$

удовлетворяют этому условию, причём первый ряд расходится, а второй сходится.

Юмор

Смех без причины — признак Д’Аламбера.

См. также

Wikimedia Foundation.2010.

Полезное

Смотреть что такое "Признак сходимости Д’Аламбера" в других словарях:

Признак сходимости д’Аламбера — Признак д’Аламбера признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г. Если для числового ряда существует такое число q, 0 < q < 1, что начиная с некоторого номера выполняется неравенство … Википедия
Признак сходимости Д'Аламбера — Признак Д’Аламбера признак сходимости числовых рядов, установлен Жаном Д’Аламбером в 1768 г. Если для числового ряда существует такое число q, 0 < q < 1, что начиная с некоторого номера выполняется неравенство то данный ряд абсолютно… … Википедия
Признак Раабе — (признак Раабе Дюамеля) признак сходимости знакоположительных числовых рядов, установленный Йозефом Людвигом Раабе (Joseph Ludwig Raabe) и независимо Жан Мари Дюамелем. Содержание 1 Формулировка 2 Формул … Википедия
Логарифмический признак сходимости — признак сходимости числовых рядов с положительными членами. Фактически этот признак сходимости сводится к сравнению исследуемого на сходимость ряда с обобщённым гармоническим рядом (рядом Дирихле) Формулировка Ряд сходится, если при … Википедия
Признак Д’Аламбера — (или Признак Даламбера) признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г. Если для числового ряда существует такое число , , что начиная с некоторого номера выполняется неравенство то данный ряд абсолютно сходится; если же … Википедия
Признак — в математике, логике то же, что и достаточное условие. В менее строгих науках слово «признак» употребляется, как описание фактов, позволяющих (согласно существующей теории и т.п.) сделать вывод о наличии интересующего явления. Примеры… … Википедия
Признак Куммера — общий признак сходимости числовых рядов с положительными членами, установленный Эрнстом Куммером. Содержание 1 Формулировка 2 Формулировка в предельной форме … Википедия
Признак Ермакова — признак сходимости числовых рядов с положительными членами, установленный Василием Ермаковым. Его специфика заключается в том, что он превосходит все прочие признаки своей чувствительностью . Эта работа опубликована в статьях: «Общая теория… … Википедия
Признак Жордана — признак сходимости рядов Фурье: если периодическая функция имеет ограниченную вариацию на отрезке , то её ряд Фурье сходится в каждой точке к числу ; если при этом функция непрерывна на отрезке … Википедия
Признак Бертрана — признак сходимости числовых рядов с положительными членами, установленный Жозефом Бертраном. Содержание 1 Формулировка 2 Формулировка в предельной форме … Википедия