Функциональная зависимость | это... Что такое Функциональная зависимость? (original) (raw)
Функциональная зависимость
Функциональная зависимость
В данной статье приведено общее определение математической функции. В средних школах и на нематематических специальностях высших учебных заведениях изучают более простое понятие числовой функции, являющееся частным случаем математической функции.
Содержание
- 1 Определения
- 2 Обозначения
- 3 Связанные определения
- 4 Свойства
- 5 Классы функций
- 6 Вариации и обобщения
- 7 Примечания
- 8 См. также
- 9 Литература
Определения
- Нестрогое определение: функция — это «закон», по которому каждому значению элемента x из некоторого множества X ставится в соответствие единственный элемент y из множества Y.
- Строгое определение: функция или отображе́ние — это бинарное отношение, обладающее свойством:

- Функция называется инъективной, если
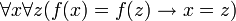
Обозначения
Связанные определения
Множество F(X) называется образом отображения F и обозначается 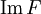 .
.
Свойства
Свойства прообразов и образов
 ;
;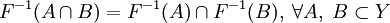 ;
;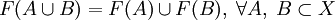 ;
;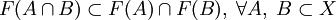 . Заметим отсутствие равенства в этом случае.
. Заметим отсутствие равенства в этом случае.
Классы функций
При необходимости можно различать отображения в зависимости от природы множеств X и Y. Если X и Y — числовые множества, такие, как 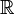 или
или 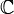 , то отображение называют функцией. Если X или Y многомерны, например,
, то отображение называют функцией. Если X или Y многомерны, например,  или
или 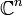 , то отображение называют ве́ктор-фу́нкцией. Если X — произвольной природы, а Y — поле, то отображение называют функциона́лом. В специальных случаях используют и другие термины: оператор, функтор, преобразование, морфизм и т. д.
, то отображение называют ве́ктор-фу́нкцией. Если X — произвольной природы, а Y — поле, то отображение называют функциона́лом. В специальных случаях используют и другие термины: оператор, функтор, преобразование, морфизм и т. д.
Вариации и обобщения
Функции нескольких аргументов
Определение функции легко обобщить на случай функции многих аргументов.
Пусть даны множества 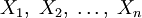 и множество Y, тогда упорядоченное множество всех кортежей
и множество Y, тогда упорядоченное множество всех кортежей 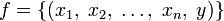 называется функцией n аргументов тогда и только тогда, когда для любых
называется функцией n аргументов тогда и только тогда, когда для любых 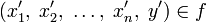 и
и 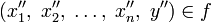 из
из 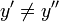 следует, что
следует, что ![x_{n}' \neq x_{n}'',\forall x\in [1,\;n]\cap\Z](https://dic.academic.ru/pictures/wiki/files/51/34b01413828b3a6b8b4f43b4c45d1446.png) .[1]
.[1]
Примечания
- ↑ Кудрявцев Л. Д. Курс математического анализа. — том 1. — М.: Высшая школа, 1981. — с. 8.
См. также
- Композиция функций
- График функции
- Сюръективность
- Инъективность
- Биективность
- Функция с множеством значений {0, 1}
- Функциональное уравнение
Литература
- Функция. Математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.
Wikimedia Foundation.2010.
Полезное
Смотреть что такое "Функциональная зависимость" в других словарях:
- функциональная зависимость — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN functional dependence … Справочник технического переводчика
- функциональная зависимость — funkcinė priklausomybė statusas T sritis fizika atitikmenys: angl. functional dependence vok. Funktionalabhängigkeit, f rus. функциональная зависимость, f pranc. dépendance fonctionnelle, f … Fizikos terminų žodynas
- Функциональная зависимость (программирование) — Функциональная зависимость концепция, лежащая в основе многих вопросов, связанных с реляционными базами данных, включая, в частности, их проектирование. Математически представляет бинарное отношение между множествами атрибутов данного… … Википедия
- полная функциональная зависимость — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN fully functional dependence … Справочник технического переводчика
- Зависимость — В Викисловаре есть статья «зависимость» Зависимость неоднозначный термин … Википедия
- ЗАВИСИМОСТЬ ФУНКЦИОНАЛЬНАЯ — см. ФУНКЦИЯ. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
- функциональная характеристика переменного резистора — Ндп. закон изменения сопротивления переменного резистора Зависимость электрического сопротивления переменного резистора от положения подвижного контакта. Примечание Функциональная характеристика может определяться аналогично через выходное… … Справочник технического переводчика
- функциональная электроннолучевая трубка — Электроннолучевой прибор, воспроизводящий в аналоговой форме функциональную зависимость между сигналами. [ГОСТ 13820 77] Тематики электровакуумные приборы EN plotting display tube FR tube fonctionnel … Справочник технического переводчика
- Функциональная семантико-стилистическая категория, ФССК — – разновидность текстовых категорий (см.), отражающая функционально стилевую дифференциацию речи (типологию текстов). ФССК – это система разноуровневых языковых средств (включая текстовые), объединенных функционально семантически и стилистически… … Стилистический энциклопедический словарь русского языка
- Функциональная характеристика переменного резистора — 49. Функциональная характеристика переменного резистора Ндп. Закон изменения сопротивления переменного резистора D. Funktioneller Widerstandsverlauf E. Resistance law F. Loi de variation Зависимость электрического сопротивления переменного… … Словарь-справочник терминов нормативно-технической документации