Момент инерции | это... Что такое Момент инерции? (original) (raw)

Момент инерции
$J = \int r^2 \mathrm dm$
Размерность	L2M
Единицы измерения
СИ	кг·м²
СГС	г·cм²

У этого термина существуют и другие значения, см. Момент.

Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения СИ: кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.

Осевой момент инерции

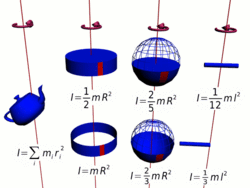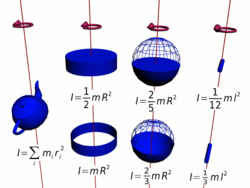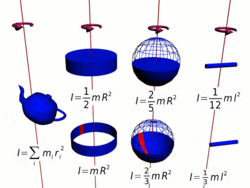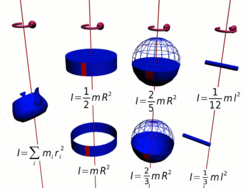
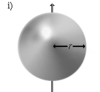
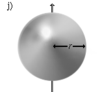
Осевые моменты инерции некоторых тел.

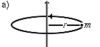
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

$J_a=\sum_{i=1}^n m_i r_i^2\,\!$ ,

где:

mi — масса _i_-й точки,
ri — расстояние от _i_-й точки до оси.

Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

$J_a=\int\limits_{(m)} r^2dm=\int\limits_{(V)} \rho r^2dV\,\!$ ,

где:

Если тело однородно, то есть его плотность всюду одинакова, то

$J_a=\rho\int\limits_{(V)} r^2dV\,\!$

Теорема Гюйгенса-Штейнера

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

~J=J_c+md^2 ,

где — полная масса тела.

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

$~J=J_c+md^2=\frac{1}{12}ml^2+m\left(\frac{l}{2}\right)^2=\frac{1}{3}ml^2$

Осевые моменты инерции некоторых тел

Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения

Тело	Описание	Положение оси a	Момент инерции Ja
	Материальная точка массы m	На расстоянии r от точки, неподвижная
	Полый тонкостенный цилиндр или кольцо радиуса r и массы m	Ось цилиндра
	Сплошной цилиндр или диск радиуса r и массы m	Ось цилиндра	$\frac{1}{2}mr^2$
	Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1	Ось цилиндра	$m \frac{r_2^2+r_1^2}{2}$
	Сплошной цилиндр длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс	${1 \over 4} m \cdot r^2 + {1 \over 12} m \cdot l^2$
	Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс	${1 \over 2} m \cdot r^2 + {1 \over 12} m \cdot l^2$
	Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его центр масс	$\frac{1}{12}ml^2$
	Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его конец	$\frac{1}{3}ml^2$
	Тонкостенная сфера радиуса r и массы m	Ось проходит через центр сферы	$\frac{2}{3}mr^2$
	Шар радиуса r и массы m	Ось проходит через центр шара	$\frac{2}{5}mr^2$
	Конус радиуса r и массы m	Ось конуса	$\frac{3}{10}mr^2$
Равнобедренный треугольник с высотой h, основанием a и массой m	Ось перпендикулярна плоскости треугольника и проходит через вершину	$\frac{1}{24}m(a^2+12h^2)$
Правильный треугольник со стороной a и массой m	Ось перпендикулярна плоскости треугольника и проходит через центр масс	$\frac{1}{12}ma^2$
Квадрат со стороной a и массой m	Ось перпендикулярна плоскости квадрата и проходит через центр масс	$\frac{1}{6}ma^2$

Вывод формул

Тонкостенный цилиндр (кольцо, обруч)

Вывод формулы

Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда

$J = \sum dJ_i = \sum R^2_idm. \qquad (1)$

Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду

$J = \sum R^2dm = R^2\sum dm = mR^2.$

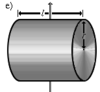
Толстостенный цилиндр (кольцо, обруч)

Вывод формулы

Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом _R_1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит

$dm = \rho dV = \rho \cdot 2\pi rhdr; \qquad dJ = r^2dm = 2\pi\rho h r^3dr.$

Момент инерции толстого кольца найдём как интеграл

$\begin{align} J & = \int^R_{R_1}dJ = 2\pi\rho h\int^R_{R_1}r^3dr = 2\pi\rho h \left. \frac{r^4}{4} \right|^R_{R_1} = \\ & = \frac{1}{2}\pi\rho h \left (R^4-R^4_1 \right) = \frac{1}{2}\pi\rho h \left (R^2-R^2_1 \right) \left (R^2+R^2_1 \right) .\end{align}$

Поскольку объём и масса кольца равны

$V = \pi \left (R^2-R^2_1 \right) h; \qquad m = \rho V = \pi\rho \left (R^2-R^2_1 \right) h,$

получаем окончательную формулу для момента инерции кольца

$J = \frac{1}{2}m \left( R^2+R^2_1 \right).$

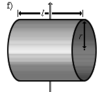
Однородный диск (сплошной цилиндр)

Вывод формулы

Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (_R_1 = 0), получим формулу для момента инерции цилиндра (диска):

$J = \frac{1}{2}mR^2.$

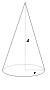
Сплошной конус

Вывод формулы

Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен

$r = \frac{Rh}{H},$

где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят

$dm = \rho V = \rho \cdot \pi r^2 dh;$

$dJ = \frac{1}{2}r^2dm = \frac{1}{2}\pi \rho r^4 dh = \frac{1}{2}\pi \rho \left( \frac{Rh}{H} \right)^4 dh;$

Интегрируя, получим

$\begin{align} J & = \int^H_0 dJ = \frac{1}{2}\pi \rho \left( \frac{R}{H} \right)^4 \int^H_0 h^4 dh = \frac{1}{2}\pi \rho \left( \frac{R}{H} \right)^4 \left. \frac{h^5}{5} \right|^H_0 = \\ & = \frac{1}{10}\pi \rho R^4H = \left( \rho \cdot \frac{1}{3}\pi R^2H \right)\frac{3}{10}R^2 = \frac{3}{10}mR^2. \end{align}$

Сплошной однородный шар

Вывод формулы

Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле

$r = \sqrt{R^2-h^2}.$

Масса и момент инерции такого диска составят

$dm = \rho dV = \rho \cdot \pi r^2 dh;$

$dJ = \frac{1}{2}r^2dm = \frac{1}{2} \pi\rho r^4 dh = \frac{1}{2} \pi\rho \left( R^2-h^2 \right)^2 dh = \frac{1}{2} \pi\rho \left( R^4-2R^2h^2+h^4 \right) dh.$

Момент инерции сферы найдём интегрированием:

$\begin{align} J & = \int^R_{-R}dJ = 2\int^R_0 dJ = \pi\rho\int^R_0 \left( R^4-2R^2h^2+h^4 \right) dh = \\ & = \pi\rho \left. \left( R^4h- \frac{2}{3}R^2h^3 + \frac{1}{5}h^5 \right) \right|^R_0 = \pi\rho \left( R^5 - \frac{2}{3}R^5 + \frac{1}{5}R^5 \right) = \frac{8}{15}\pi \rho R^5 = \\ & = \left( \frac{4}{3}\pi R^3 \rho \right) \cdot \frac{2}{5} R^2 = \frac{2}{5} m R^2. \end{align}$

Тонкостенная сфера

Вывод формулы

Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:

$J_0 = \frac{2}{5}MR^2 = \frac{8}{15}\pi \rho R^5.$

Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.

$\begin{align} J & = \frac{dJ_0}{dR}dR = \frac{d}{dR} \left( \frac{8}{15}\pi \rho R^5 \right) dR = \\ & = \frac{8}{3}\pi \rho R^4 dR = \left( \rho \cdot 4 \pi R^2 dR \right) \frac{2}{3} R^2 = \frac{2}{3} mR^2 \end{align}$

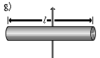
Тонкий стержень (ось проходит через центр)

Вывод формулы

Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна

$dm = \frac{mdr}{l}; \qquad dJ = r^2dm = \frac{mr^2dr}{l}.$

Интегрируя, получим

$J = \int^{l/2}_{-l/2} dJ = 2\int^{l/2}_0 dJ = \frac{2m}{l}\int^{l/2}_0 r^2dr = \frac{2m}{l} \left. \frac{r^3}{3} \right|^{l/2}_0 = \frac{2m}{l} \frac{l^3}{24} = \frac{1}{12}ml^2.$

Тонкий стержень (ось проходит через конец)

Вывод формулы

При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен

$J = J_0+mr^2 = J_0+m \left( \frac{l}{2} \right)^2 = \frac{1}{12}ml^2 + \frac{1}{4}ml^2 = \frac{1}{3}ml^2.$

Безразмерные моменты инерции планет и их спутников[1][2]

Безразмерные моменты инерции планет и их спутников

Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному _mr_2). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра. [3][4]

Центробежный момент инерции

Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:

$J_{xy}=\int\limits_{(m)} xydm=\int\limits_{(V)} xy\rho dV\,\!$

$J_{xz}=\int\limits_{(m)} xzdm=\int\limits_{(V)} xz\rho dV\,\!$

$J_{yz}=\int\limits_{(m)} yzdm=\int\limits_{(V)} yz\rho dV\,\!$

где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.

Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела.

Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.

Геометрический момент инерции

Геометрический момент инерции — геометрическая характеристика сечения вида

$J_y = \int_{F}^{} z^2dF$

$J_z = \int_{F}^{} y^2dF$

где — расстояние от центральной оси y(z) до любой элементарной площадки относительно нейтральной оси.

Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для вычисления радиуса инерции, прогиба балки, подбора сечения балок, колонн и др.

Единица измерения СИ — м4. В строительных расчетах, литературе и сортаментах металлопроката в частности указывается в см4.

Из него выражается момент сопротивления сечения:

$W=\frac{J}{r_{max}}$ .

Геометрические моменты инерции некоторых фигур
Прямоугольника высотой и шириной :	$J_y =\frac{bh^3}{12}$ $J_z =\frac{hb^3}{12}$
Прямоугольного коробчатого сечения высотой и шириной по внешним контурам и , а по внутренним и соответственно	$J_z =\frac{BH^3}{12}-\frac{bh^3}{12}=\frac{1}{12}(BH^3-bh^3)$ $J_y =\frac{HB^3}{12}-\frac{hb^3}{12}=\frac{1}{12}(HB^3-hb^3)$
Круга диаметром	$J_y=J_z =\frac{\pi d^4}{64}$

Центральный момент инерции

Центральный момент инерции ~J_O (или момент инерции относительно точки O) — это величина

$J_a=\int\limits_{(m)} r^2dm=\int\limits_{(V)} \rho r^2dV\,\!$ ,

где:

Центральный момент инерции можно выразить через главные осевые или центробежные моменты инерции: $~J_O=J_{xy}+J_{yz}+J_{xz}=\frac{1}{2}\left(J_x+J_y+J_z\right)$ .

Тензор инерции и эллипсоид инерции

Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором $~\vec s = \left \Vert s_x , s_y , s_z \right \Vert^T ,\left \vert \vec s \right \vert=1$ , можно представить в виде квадратичной (билинейной) формы:

$~ I_s= \vec s^T \cdot \hat J \cdot \vec s \qquad$ (1),

где $~ \hat J$ — тензор инерции. Матрица тензора инерции симметрична, имеет размеры $~ 3 \times 3$ и состоит из компонент центробежных моментов:

$~ \hat J = \left \Vert \begin{array}{ccc} J_{xx} & -J_{xy} & -J_{xz} \\ -J_{yx} & J_{yy} & -J_{yz} \\-J_{zx} & -J_{zy} & J_{zz} \end{array} \right \Vert$ , $~ J_{xy}= J_{yx}, J_{xz}= J_{zx}, J_{zy}= J_{yz},$
$~J_{xx}=\int\limits_{(m)} (y^2+z^2)dm , J_{yy}=\int\limits_{(m)} (x^2+z^2)dm, J_{zz}=\int\limits_{(m)} (x^2+y^2)dm$ .

Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора $~ \hat J$ :
$~ \hat J_d = \hat Q^T \cdot \hat J \cdot \hat Q ;$ $~ \hat J_d = \left \Vert \begin{array}{ccc} J_{X} & 0 & 0 \\ 0 & J_{Y} & 0 \\0 & 0 & J_{Z} \end{array} \right \Vert$ ,
где $~ \hat Q$ — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины $~ J_{X},J_{Y},J_{Z}$ — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:

$~ I_s= J_{X} \cdot s_x^2 +J_{Y} \cdot s_y^2 + J_{Z} \cdot s_z^2$ ,

откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на ~ I_s

$~ \left ( {s_x \over \sqrt {I_s}}\right )^2 \cdot J_{X} + \left ( {s_y \over \sqrt {I_s}}\right )^2 \cdot J_{Y} + \left ( {s_z \over \sqrt {I_s}}\right )^2 \cdot J_{Z} =1$

и произведя замены:

$~ \xi= {s_x \over \sqrt {I_s}}, \eta= {s_y \over \sqrt {I_s}}, \zeta= {s_z \over \sqrt {I_s}}$ ,

получаем канонический вид уравнения эллипсоида в координатах $~ \xi \eta \zeta$ :

$~ \xi^2 \cdot J_{X} + \eta^2 \cdot J_{Y} + \zeta^2 \cdot J_{Z} =1$

Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:

$~ r^2 = \xi^2 + \eta^2 + \zeta^2 = \left ( {s_x \over \sqrt {I_s}}\right )^2 + \left ( {s_y \over \sqrt {I_s}}\right )^2 + \left ( {s_z \over \sqrt {I_s}}\right )^2 = {1 \over I_s}$

См. также

Примечания

↑ Planetary Fact Sheet
↑ Showman, Adam P.; Malhotra, Renu (1999). «The Galilean Satellites» (PDF). Science 286 (5437): 77–84. DOI:10.1126/science.286.5437.77. PMID 10506564.
↑ Галкин И.Н. Внеземная сейсмология. — М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X
↑ Пантелеев В. Л. Физика Земли и планет. Гл. 3.4 — Гравитационное поле планеты

Литература

Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.) http://www.alleng.ru/d/phys/phys108.htm
Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997. http://nature.web.ru/db/msg.html?mid=1186208&s=120000000
Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с. http://www.alleng.ru/d/phys/phys99.htm
Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm
Беляев Н. М., Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.

Ссылки

	Момент инерции на Викискладе?