Релятивистская масса | это... Что такое Релятивистская масса? (original) (raw)

Эта статья о физической величине. Статью об автогонщике см. Масса, Фелипе

Ма́сса — одна из важнейших физических величин. Первоначально (XVII–XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационные свойства — вес. В современной физике понятие «количество вещества» имеет другой смысл, а под массой понимают два различных свойства физического объекта:

Теоретически, гравитационная и инертная масса равны, поэтому в большинстве случаев просто говорят о массе, не уточняя какую из них имеют в виду.

Масса тела не зависит от того, какие внешние силы и в какой момент на это тело действуют.

Содержание

Исследование единства понятия массы

Гравитационная масса — характеристика материальной точки при анализе в классической механике, которая полагается причиной гравитационного взаимодействия тел, в отличие от инертной массы, которая определяет динамические свойства тел.

Как установлено экспериментально, эти две массы пропорциональны друг другу. Не было обнаружено никаких отклонений от этого закона, поэтому новых единиц измерения для инерционной массы не вводят (используют единицы измерения гравитационной массы) и коэффициент пропорциональности считают равным единице, что позволяет говорить и о равенстве инертной и гравитационной масс.

Можно сказать, что первая проверка пропорциональности двух видов массы была выполнена Галилео Галилеем, который открыл универсальность свободного падения. Согласно опытам Галилея по наблюдению свободного падения тел, все тела, независимо от их массы и материала, падают с одинаковым ускорением свободного падения. Сейчас эти опыты можно трактовать так: увеличение силы, действующей на более массивное тело со стороны гравитационного поля Земли, полностью компенсируется увеличением его инертных свойств. Следовательно, гравитационная масса пропорциональна инертной массе[1]

На равенство инертной и гравитационной масс обратил внимание ещё Ньютон, он же впервые доказал, что они отличаются не более чем на 0,1 % (иначе говоря, равны с точностью до 10−3).. На сегодняшний день это равенство экспериментально проверено с очень высокой степенью точности (3×10−13).

Фактически, равенство гравитационной и инертной масс было сформулировано А. Эйнштейном в виде слабого принципа эквивалентности — составной части принципов эквивалентности, положенных в основу общей теории относительности. Существует также сильный принцип эквивалентности — по которому в свободно падающей системе локально выполняется специальная теория относительности. Он на сегодняшний день проверен со значительно меньшей точностью.

В классической механике — масса есть величина аддитивная (масса системы равна сумме масс составляющих её тел) и инвариантная относительно смены системы отсчёта. В релятивистской механике масса неаддитивная величина, но тоже инвариантная, и хотя здесь под массой понимается абсолютная величина 4-вектора энергии-импульса, лоренц-инвариантная.

Введение так называемой релятивистской массы, зависящей от величины скорости тела в рассматриваемой системе отсчёта, использовалось в ранних работах по теории относительности. В настоящее время термины «релятивистская масса» и «масса покоя» считаются устаревшими[2].

Определение массы

В СТО масса тела m определяется из уравнения релятивистской динамики [3]:

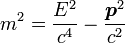m^2 = \frac{E^2}{c^4} - \frac{\boldsymbol{p}^2}{c^2},

где E — полная энергия свободного тела, p — его импульс, c — скорость света.

Определённая выше масса является релятивистским инвариантом, то есть она одна и та же во всех системах отсчёта. Если перейти в систему отсчёта, где тело покоится, то 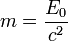m = \frac{E_0}{c^2} — масса определяется энергией покоя.

Следует однако отметить, что частицы с нулевой инвариантной массой (фотон, гравитон…) двигаются в вакууме со скоростью света (c ≈ 300000 км/сек) и поэтому не обладают системой отсчёта, в которой бы покоились.

Масса составных и нестабильных систем

Инвариантная масса элементарной частицы постоянна, и одинакова у всех частиц данного типа и их античастиц. Однако, масса массивных тел, составленных из нескольких элементарных частиц (например, ядра или атома) может зависеть от их внутреннего состояния.

Для системы, подверженной распаду (например, радиоактивному), величина энергии покоя определена лишь с точностью до постоянной Планка, делённой на время жизни: 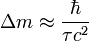\Delta m \approx \frac{\hbar}{\tau c^2}. При описании такой системы при помощи квантовой механики удобно считать массу комплексной, с мнимой частью равной означенному Δm.

Единицы массы

В системе СИ масса измеряется в килограммах. В системе СГС используются граммы. Иногда используются также другие единицы измерения массы.

Измерение массы

Основная статья: Весы

Исторический очерк

Понятие массы было введено в физику Ньютоном, до этого естествоиспытатели оперировали с понятием веса. В труде «Математические начала натуральной философии» Ньютон сначала определил «количество материи» в физическом теле как произведение его плотности на объём. Далее он указал, что в том же смысле будет использовать термин масса. Наконец, Ньютон вводит массу в законы физики: сначала во второй закон Ньютона (через количество движения), а затем — в закон тяготения, откуда сразу следует, что масса пропорциональна весу [4].

Фактически Ньютон использует только два понимания массы: как меры инерции и источника тяготения. Толкование её как меры «количества материи» — не более чем наглядная иллюстрация, и оно подверглось критике ещё в XIX веке как нефизическое и бессодержательное.

Долгое время одним из главных законов природы считался закон сохранения массы. Однако в XX веке выяснилось, что этот закон является ограниченным вариантом закона сохранения энергии, и во многих ситуациях не соблюдается.

Примечания

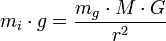
  1. ↑ Например, это видно из закона всемирного тяготения Ньютона (связывающего силу и гравитационную массу), второго закона Ньютона (связывающего силу с массой инерционной), и замеченной Галилеем независимости ускорения свободного падения от материала: m_i \cdot g = \frac{m_g \cdot M \cdot G}{r^2}
  2. ↑ См., например, дискуссию в «Успехах физических наук», вып.12, 2000: письмо Окуня).
  3. ↑ Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7, § 9. Энергия и импульс.
  4. ↑ Спасский Б. И.. История физики. М., «Высшая школа», 1977, том I, с. 135—137.

Литература

См. также

Ссылки

Wikimedia Foundation.2010.