Геометрия Лобачевского | это... Что такое Геометрия Лобачевского? (original) (raw)

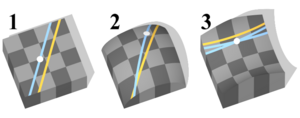
(1) евклидова геометрия; (2) геометрия Римана; (3) геометрия Лобачевского

Геометрия Лобачевского (гиперболическая геометрия) — одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского.

Евклидова аксиома о параллельных (точнее, одно из эквивалентных ей утверждений) гласит:

Через точку, не лежащую на данной прямой, проходит не более одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её.

В геометрии Лобачевского, вместо неё принимается следующая аксиома:

Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.

Широко распространено заблуждение, что в геометрии Лобачевского параллельные прямые пересекаются[1]. Геометрия Лобачевского имеет обширные применения как в математике, так и в физике. Историческое и философское её значение состоит в том, что её построением Лобачевский показал возможность геометрии, отличной от евклидовой, что знаменовало новую эпоху в развитии геометрии, математики и науки вообще.

Содержание

История

Попытки доказательства пятого постулата

Отправным пунктом геометрии Лобачевского послужил V постулат Евклида — аксиома, эквивалентная аксиоме о параллельных. Он входил в список постулатов в «Началах» Евклида. Относительная сложность и неинтуитивность его формулировки вызывала ощущение его вторичности и порождала попытки вывести его как теорему из остальных постулатов Евклида.

Среди многих пытавшихся доказать пятый постулат были, в частности, следующие крупные учёные.

При этих попытках доказательства пятого постулата математики вводили (явно или неявно) некоторое новое утверждение, казавшееся им более очевидным.

Были предприняты попытки использовать доказательство от противного:

Наконец, стало возникать понимание о том, что возможно построение теории, основанной на противоположном постулате:

Создание неевклидовой геометрии

Лобачевский в работе «О началах геометрии» (1829), первой его печатной работе по неевклидовой геометрии, ясно заявил, что V постулат не может быть доказан на основе других посылок евклидовой геометрии, и что допущение постулата, противоположного постулату Евклида, позволяет построить геометрию столь же содержательную, как и евклидова, и свободную от противоречий.

Одновременно и независимо к аналогичным выводам пришёл Янош Бойяи, а Карл Фридрих Гаусс пришёл к таким выводам ещё раньше. Однако труды Бойяи не привлекли внимания, и он вскоре оставил эту тему, а Гаусс вообще воздерживался от публикаций, и о его взглядах можно судить лишь по нескольким письмам и дневниковым записям. Например, в письме 1846 года астроному Г. Х. Шумахеру Гаусс так отозвался о работе Лобачевского:

Это сочинение содержит в себе основания той геометрии, которая должна была бы иметь место и притом составляла бы строго последовательное целое, если бы евклидова геометрия не была бы истинной… Лобачевский называет ее «воображаемой геометрией»; Вы знаете, что уже 54 года (с 1792 г.) я разделяю те же взгляды с некоторым развитием их, о котором не хочу здесь упоминать; таким образом, я не нашёл для себя в сочинении Лобачевского ничего фактически нового. Но в развитии предмета автор следовал не по тому пути, по которому шёл я сам; оно выполнено Лобачевским мастерски в истинно геометрическом духе. Я считаю себя обязанным обратить Ваше внимание на это сочинение, которое, наверное, доставит Вам совершенно исключительное наслаждение.[3]

В итоге Лобачевский выступил как первый наиболее яркий и последовательный пропагандист новой геометрии. Хотя геометрия Лобачевского развивалась как умозрительная теория, и сам Лобачевский называл её «воображаемой геометрией», тем не менее именно он впервые открыто предложил её не как игру ума, а как возможную и полезную теорию пространственных отношений. Однако доказательство её непротиворечивости было дано позже, когда были указаны её интерпретации (модели).

Утверждение геометрии Лобачевского

Лобачевский умер в 1856 году. Спустя несколько лет была опубликована переписка Гаусса, в том числе несколько восторженных отзывов о геометрии Лобачевского, и это привлекло внимание к трудам Лобачевского. Появляются переводы их на французский и итальянский языки, комментарии видных геометров. Публикуется и труд Бойяи.

В 1868 году выходит статья Э. Бельтрами об интерпретациях геометрии Лобачевского. Бельтрами определил метрику плоскости Лобачевского и доказал, что она имеет всюду постоянную отрицательную кривизну. Такая поверхность тогда уже была известна — это псевдосфера Миндинга. Бельтрами сделал вывод, что локально плоскость Лобачевского изометрична участку псевдосферы (см. ниже). Окончательно непротиворечивость геометрии Лобачевского была доказана в 1871 году, после появления модели Клейна.

Вейерштрасс посвящает геометрии Лобачевского специальный семинар в Берлинском университете (1870). Казанское физико-математическое общество организует издание полного собрания сочинений Лобачевского, а в 1893 году столетие русского математика отмечается в международном масштабе.

Модели

Модели геометрии Лобачевского дали доказательство её непротиворечивости, точнее показали, что геометрия Лобачевского столь же непротиворечива, как геометрия Евклида.

Сам Лобачевский дал основы своей аналитической геометрии, и тем самым он уже фактически наметил такую модель. Он также заметил что орисфера в пространстве Лобачевского изометрична евклидовой плоскости, тем самым фактически предложил обратную модель. Тем не менее, само понятие о модели прояснилось в работах Клейна и других.

Псевдосфера

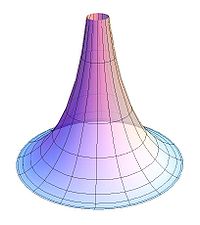
Псевдосфера

Итальянский математик Э. Бельтрами в 1868 году заметил, что геометрия на куске плоскости Лобачевского совпадает с геометрией на поверхностях постоянной отрицательной кривизны, простейший пример которых представляет псевдосфера. Если точкам и прямым на конечном куске плоскости Лобачевского сопоставлять точки и кратчайшие линии (геодезические) на псевдосфере и движению в плоскости Лобачевского сопоставлять перемещение фигуры по псевдосфере с изгибанием, то есть деформацией, сохраняющей длины, то всякой теореме геометрии Лобачевского будет отвечать факт, имеющий место на псевдосфере. При этом длины, углы, площади понимаются в смысле естественного измерения их на псевдосфере.

Однако здесь даётся только локальная интерпретация геометрии, то есть на ограниченном участке, а не на всей плоскости Лобачевского.

Модель Клейна

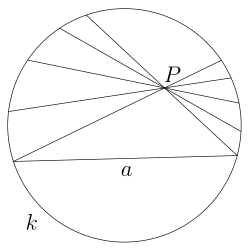
Через точку Р проходит бесконечно много «прямых», не пересекающих «прямой» а

В 1871 году Клейн предложил первую полноценную модель плоскости Лобачевского.

Плоскостью служит внутренность круга, прямой — хорда круга без концов, а точкой — точка внутри круга. «Движением» назовём любое преобразование круга в самого себя, которое переводит хорды в хорды. Соответственно, равными называются фигуры внутри круга, переводящиеся одна в другую такими преобразованиями. Тогда оказывается, что любой геометрический факт, описанный на таком языке, представляет теорему или аксиому геометрии Лобачевского. Иными словами, всякое утверждение геометрии Лобачевского на плоскости есть не что иное, как утверждение евклидовой геометрии, относящееся к фигурам внутри круга, лишь пересказанное в указанных терминах. Евклидова аксиома о параллельных здесь явно не выполняется, так как через точку P, не лежащую на данной хорде а (то есть «прямой»), проходит сколько угодно не пересекающих её хорд («прямых») (например, b, b').

В этой модели расстояние между точками A и B на хорде NM определяется через двойное отношение

\ln\left(\frac{AN}{AM}\frac{BM}{BN}\right)

Модель Пуанкаре

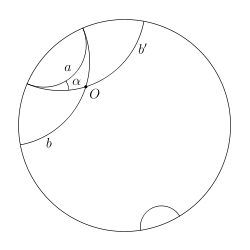
Позже Пуанкаре, в связи с задачами теории функций комплексного переменного дал другую модель. За плоскость Лобачевского принимается внутренность круга, прямыми считаются дуги окружностей, перпендикулярных окружности данного круга, и его диаметры, движениями — преобразования, получаемые комбинациями инверсий относительно окружностей, дуги которых служат прямыми.

Модель Пуанкаре замечательна тем, что в ней углы изображаются обычными углами.

Поверхность постоянной отрицательной кривизны

Другое аналитическое определение геометрии Лобачевского состоит в том, что геометрия Лобачевского определяется как геометрия риманова пространства постоянной отрицательной кривизны. Это определение было фактически дано ещё в 1854 году Риманом и включало модель геометрии Лобачевского как геометрии на поверхностях постоянной кривизны. Однако Риман не связал прямо своих построений с геометрией Лобачевского, а его доклад, в котором он о них сообщил, не был понят и был опубликован лишь после его смерти (в 1868 году).

Содержание геометрии Лобачевского

Угол параллельности

Лобачевский строил свою геометрию, отправляясь от основных геометрических понятий и своей аксиомы, и доказывал теоремы геометрическим методом, подобно тому, как это делается в геометрии Евклида. Основой служила теория параллельных линий, так как именно здесь начинается отличие геометрии Лобачевского от геометрии Евклида. Все теоремы, не зависящие от аксиомы о параллельных, являются общими для обеих геометрий; они образуют так называемую абсолютную геометрию, к которой относятся, например, теоремы о равенстве треугольников. Вслед за теорией параллельных строились другие разделы, включая тригонометрию и начала аналитической и дифференциальной геометрии.

Приведём (в современных обозначениях) несколько фактов геометрии Лобачевского, отличающих её от геометрии Евклида и установленных самим Лобачевским.

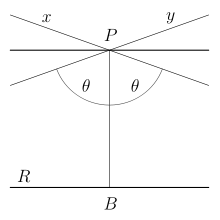
Через точку P, не лежащую на данной прямой R (см. рисунок), проходит бесконечно много прямых, не пересекающих R и находящихся с ней в одной плоскости; среди них есть две крайние x, y, которые и называются параллельными прямой R в смысле Лобачевского. В моделях Клейна (Пуанкаре) они изображаются хордами (дугами окружностей), имеющими с хордой (дугой) R общий конец (который по определению модели исключается, так что эти прямые не имеют общих точек).

Угол \theta между перпендикуляром PB из P на R и каждой из параллельных (называемый углом параллельности) по мере удаления точки P от прямой убывает от 90° до 0° (в модели Пуанкаре углы в обычном смысле совпадают с углами в смысле Лобачевского, и потому на ней этот факт можно видеть непосредственно). Параллель x с одной стороны (а y с противоположной) асимптотически приближается к а, а с другой — бесконечно от неё удаляется (в моделях расстояния определяются сложно, и потому этот факт непосредственно не виден).

Для точки, находящейся от заданной прямой на расстоянии PB = a (см. рисунок), Лобачевский дал формулу для угла параллельности П(a)[4]:

\theta = \Pi(a) = 2 \operatorname{arctg}~e^{-\frac{a}{q}}

Здесь q — некоторая постоянная, связанная с кривизной пространства Лобачевского. Она может служить абсолютной единицей длины аналогично тому, как в сферической геометрии особое положение занимает радиус сферы.

Если прямые имеют общий перпендикуляр, то они бесконечно расходятся в обе стороны от него. К любой из них можно восстановить перпендикуляры, которые не достигают другой прямой.

В геометрии Лобачевского не существует подобных, но неравных треугольников; треугольники равны, если их углы равны.

Сумма углов всякого треугольника меньше \pi и может быть сколь угодно близкой к нулю. Это непосредственно видно на модели Пуанкаре. Разность \delta = \pi-(\alpha + \beta + \gamma), где \alpha, \beta, \gamma — углы треугольника, пропорциональна его площади:

S = q^2 \cdot \delta

Из формулы видно, что существует максимальная площадь треугольника, и это конечное число: \pi q^2 .

Линия равных расстояний от прямой не есть прямая, а особая кривая, называемая эквидистантой, или гиперциклом.

Предел окружностей бесконечно увеличивающегося радиуса не есть прямая, а особая кривая, называемая предельной окружностью, или орициклом.

Предел сфер бесконечно увеличивающегося радиуса не есть плоскость, а особая поверхность — предельная сфера, или орисфера; замечательно, что на ней имеет место евклидова геометрия. Это служило Лобачевскому основой для вывода формул тригонометрии.

Длина окружности не пропорциональна радиусу, а растёт быстрее. В частности, в геометрии Лобачевского число \pi не может быть определено как отношение длины окружности к её диаметру.

Чем меньше область в пространстве или на плоскости Лобачевского, тем меньше геометрические соотношения в этой области отличаются от соотношений евклидовой геометрии. Можно сказать, что в бесконечно малой области имеет место евклидова геометрия. Например, чем меньше треугольник, тем меньше сумма его углов отличается от \pi; чем меньше окружность, тем меньше отношение её длины к радиусу отличается от 2\pi, и т. п. Уменьшение области формально равносильно увеличению единицы длины, поэтому при безграничном увеличении единицы длины формулы геометрии Лобачевского переходят в формулы евклидовой геометрии. Евклидова геометрия есть в этом смысле «предельный» случай геометрии Лобачевского.

Заполнение плоскости и пространства правильными политопами

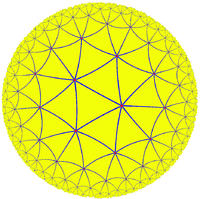
Замощение плоскости Лобачевского правильными треугольниками ({3;7})

Плоскость Лобачевского может быть замощена не только правильными треугольниками, квадратами и шестиугольниками, но и любыми другими правильными многоугольниками. При этом в одной вершине паркета должно сходиться не менее 7 треугольников, 5 квадратов, 4 пяти- и шестиугольников и 3 многоугольников с числом сторон более 6. Каждое замощение \left\{ N;M \right\} (в одной вершине сходится M N-угольников) требует строго определённого размера единичного N-угольника, в частности, его площадь должна равняться:

S_{ \left\{ N;M \right\} } = q^2 \pi \left( N - 2 - 2\frac{N}{M} \right)

Заполнение пространства Лобачевского правильными додекаэдрами ({5,3,4})

В отличие от обычного пространства, которое можно заполнить правильными многогранниками только одним способом (по 8 кубов в вершине), трёхмерное пространство Лобачевского можно заполнить правильными многогранниками четырьмя способами:

Кроме этого, существует 11 способов заполнить пространство Лобачевского правильными мозаичными орисферами.

Приложения

~x^2 + y^2 + z^2 = c^2t^2

при делении на t^2, то есть для скорости света, даёт

~v_x^2 + v_y^2 + v_z^2 = c^2

— уравнение сферы в пространстве с координатами v_x, v_y, v_z — составляющими скорости по осям х, у, z (в «пространстве скоростей»). Преобразования Лоренца сохраняют эту сферу и, так как они линейны, переводят прямые пространства скоростей в прямые. Следовательно, согласно модели Клейна, в пространстве скоростей внутри сферы радиуса с, то есть для скоростей, меньших скорости света, имеет место геометрия Лобачевского.

См. также

Примечания

  1. ↑ Параллельные прямые — в мифологии, реальности и математике Успенский В. А. Апология математики, глава 8
  2. ↑ Розенфельд Б. А. Доказательства пятого постулата Евклида средневековых математиков Хасана ибн ал-Хайсама и Льва Герсонида. — М.: ИМИ, 1958. — Т. XI. — С. 733—742.
  3. ↑ Об основаниях геометрии. Сборник классических работ по геометрии Лобачевского и развитию ее идей. М.: Гостехиздат, 1956, С.119-120.
  4. ↑ Колмогоров А. Н., Юшкевич А. П. (ред.) Математика XIX века. М.: Наука, том II, с. 62.

Труды основоположников

Литература

Ссылки