ClassificationSVM - Support vector machine (SVM) for one-class and binary classification - MATLAB (original) (raw)
Support vector machine (SVM) for one-class and binary classification
Description
ClassificationSVM is a support vector machine (SVM) classifier for one-class and two-class learning. Trained ClassificationSVM classifiers store training data, parameter values, prior probabilities, support vectors, and algorithmic implementation information. Use these classifiers to perform tasks such as fitting a score-to-posterior-probability transformation function (see fitPosterior) and predicting labels for new data (see predict).
Creation
Create a ClassificationSVM object by using fitcsvm.
Properties
SVM Properties
This property is read-only.
Data Types: single | double
This property is read-only.
Data Types: single | double
This property is read-only.
Bias term, specified as a scalar.
Data Types: single | double
This property is read-only.
Box constraints, specified as a numeric vector of _n_-by-1 box constraints. n is the number of observations in the training data (see the NumObservations property).
If you remove duplicates by using the RemoveDuplicates name-value pair argument of fitcsvm, then for a given set of duplicate observations, MATLAB sums the box constraints and then attributes the sum to one observation. MATLAB attributes the box constraints of 0 to all other observations in the set.
Data Types: single | double
This property is read-only.
Caching information, specified as a structure array. The caching information contains the fields described in this table.
| Field | Description |
|---|---|
| Size | The cache size (in MB) that the software reserves to train the SVM classifier. For details, see 'CacheSize'. |
| Algorithm | The caching algorithm that the software uses during optimization. Currently, the only available caching algorithm is Queue. You cannot set the caching algorithm. |
Display the fields of CacheInfo by using dot notation. For example, Mdl.CacheInfo.Size displays the value of the cache size.
Data Types: struct
This property is read-only.
Support vector indicator, specified as an _n_-by-1 logical vector that flags whether a corresponding observation in the predictor data matrix is a Support Vector. n is the number of observations in the training data (see NumObservations).
If you remove duplicates by using the RemoveDuplicates name-value pair argument of fitcsvm, then for a given set of duplicate observations that are support vectors, IsSupportVector flags only one observation as a support vector.
Data Types: logical
This property is read-only.
Data Types: struct
This property is read-only.
Data Types: single | double
This property is read-only.
Proportion of outliers in the training data, specified as a numeric scalar.
Data Types: double
This property is read-only.
Optimization routine used to train the SVM classifier, specified as 'ISDA', 'L1QP', or 'SMO'. For more details, see 'Solver'.
This property is read-only.
Data Types: single | double
This property is read-only.
Data Types: single | double
Other Classification Properties
This property is read-only.
Categorical predictor indices, specified as a vector of positive integers. CategoricalPredictors contains index values indicating that the corresponding predictors are categorical. The index values are between 1 and p, where p is the number of predictors used to train the model. If none of the predictors are categorical, then this property is empty ([]).
Data Types: double
This property is read-only.
Unique class labels used in training, specified as a categorical or character array, logical or numeric vector, or cell array of character vectors.ClassNames has the same data type as the class labelsY. (The software treats string arrays as cell arrays of character vectors.) ClassNames also determines the class order.
Data Types: single | double | logical | char | cell | categorical
This property is read-only.
Data Types: double
This property is read-only.
Data Types: cell
This property is read-only.
Training data gradient values, specified as a numeric vector. The length of Gradient is equal to the number of observations (NumObservations).
Data Types: single | double
This property is read-only.
Parameters used to train the ClassificationSVM model, specified as an object. ModelParameters contains parameter values such as the name-value pair argument values used to train the SVM classifier. ModelParameters does not contain estimated parameters.
Access the properties of ModelParameters by using dot notation. For example, access the initial values for estimatingAlpha by usingMdl.ModelParameters.Alpha.
This property is read-only.
Data Types: single | double
This property is read-only.
Number of observations in the training data stored in X and Y, specified as a numeric scalar.
Data Types: double
This property is read-only.
Predictor variable names, specified as a cell array of character vectors. The order of the elements in PredictorNames corresponds to the order in which the predictor names appear in the training data.
Data Types: cell
This property is read-only.
Data Types: single | double
This property is read-only.
Response variable name, specified as a character vector.
Data Types: char
This property is read-only.
Rows of the original training data stored in the model, specified as a logical vector. This property is empty if all rows are stored inX and Y.
Data Types: logical
Data Types: char | function_handle
This property is read-only.
Data Types: single | double
This property is read-only.
Observation weights used to train the SVM classifier, specified as an _n_-by-1 numeric vector. n is the number of observations (see NumObservations).
fitcsvm normalizes the observation weights specified in the 'Weights' name-value pair argument so that the elements of W within a particular class sum up to the prior probability of that class.
Data Types: single | double
This property is read-only.
Unstandardized predictors used to train the SVM classifier, specified as a numeric matrix or table.
Each row of X corresponds to one observation, and each column corresponds to one variable.
Data Types: single | double
This property is read-only.
Class labels used to train the SVM classifier, specified as a categorical or character array, logical or numeric vector, or cell array of character vectors. Y is the same data type as the input argument Y of fitcsvm. (The software treats string arrays as cell arrays of character vectors.)
Each row of Y represents the observed classification of the corresponding row of X.
Data Types: single | double | logical | char | cell | categorical
Convergence Control Properties
This property is read-only.
Convergence information, specified as a structure array.
| Field | Description |
|---|---|
| Converged | Logical flag indicating whether the algorithm converged (1 indicates convergence). |
| ReasonForConvergence | Character vector indicating the criterion the software uses to detect convergence. |
| Gap | Scalar feasibility gap between the dual and primal objective functions. |
| GapTolerance | Scalar feasibility gap tolerance. Set this tolerance, for example to 1e-2, by using the name-value pair argument 'GapTolerance',1e-2 of fitcsvm. |
| DeltaGradient | Scalar-attained gradient difference between upper and lower violators |
| DeltaGradientTolerance | Scalar tolerance for the gradient difference between upper and lower violators. Set this tolerance, for example to 1e-2, by using the name-value pair argument 'DeltaGradientTolerance',1e-2 of fitcsvm. |
| LargestKKTViolation | Maximal scalar Karush-Kuhn-Tucker (KKT) violation value. |
| KKTTolerance | Scalar tolerance for the largest KKT violation. Set this tolerance, for example, to 1e-3, by using the name-value pair argument 'KKTTolerance',1e-3 of fitcsvm. |
| History | Structure array containing convergence information at set optimization iterations. The fields are:NumIterations: numeric vector of iteration indices for which the software records convergence informationGap: numeric vector of Gap values at the iterationsDeltaGradient: numeric vector of DeltaGradient values at the iterationsLargestKKTViolation: numeric vector of LargestKKTViolation values at the iterationsNumSupportVectors: numeric vector indicating the number of support vectors at the iterationsObjective: numeric vector of Objective values at the iterations |
| Objective | Scalar value of the dual objective function. |
Data Types: struct
This property is read-only.
Number of iterations required by the optimization routine to attain convergence, specified as a positive integer.
To set the limit on the number of iterations to 1000, for example, specify 'IterationLimit',1000 when you train the SVM classifier using fitcsvm.
Data Types: double
This property is read-only.
Number of iterations between reductions of the active set, specified as a nonnegative integer.
To set the shrinkage period to 1000, for example, specify 'ShrinkagePeriod',1000 when you train the SVM classifier using fitcsvm.
Data Types: single | double
Hyperparameter Optimization Properties
This property is read-only.
Description of the cross-validation optimization of hyperparameters, specified as a BayesianOptimization object or a table of hyperparameters and associated values. This property is nonempty when the 'OptimizeHyperparameters' name-value pair argument of fitcsvm is nonempty at creation. The value of HyperparameterOptimizationResults depends on the setting of the Optimizer field in the HyperparameterOptimizationOptions structure of fitcsvm at creation, as described in this table.
| Value of Optimizer Option | Value of HyperparameterOptimizationResults |
|---|---|
| "bayesopt" (default) | Object of class BayesianOptimization |
| "gridsearch" or "randomsearch" | Table of hyperparameters used, observed objective function values (cross-validation loss), and rank of observations from lowest (best) to highest (worst) |
Object Functions
| compact | Reduce size of machine learning model |
|---|---|
| compareHoldout | Compare accuracies of two classification models using new data |
| crossval | Cross-validate machine learning model |
| discardSupportVectors | Discard support vectors for linear support vector machine (SVM) classifier |
| edge | Find classification edge for support vector machine (SVM) classifier |
| fitPosterior | Fit posterior probabilities for support vector machine (SVM) classifier |
| gather | Gather properties of Statistics and Machine Learning Toolbox object from GPU |
| incrementalLearner | Convert binary classification support vector machine (SVM) model to incremental learner |
| lime | Local interpretable model-agnostic explanations (LIME) |
| loss | Find classification error for support vector machine (SVM) classifier |
| margin | Find classification margins for support vector machine (SVM) classifier |
| partialDependence | Compute partial dependence |
| plotPartialDependence | Create partial dependence plot (PDP) and individual conditional expectation (ICE) plots |
| predict | Classify observations using support vector machine (SVM) classifier |
| resubEdge | Resubstitution classification edge |
| resubLoss | Resubstitution classification loss |
| resubMargin | Resubstitution classification margin |
| resubPredict | Classify training data using trained classifier |
| resume | Resume training support vector machine (SVM) classifier |
| shapley | Shapley values |
| testckfold | Compare accuracies of two classification models by repeated cross-validation |
Examples
Load Fisher's iris data set. Remove the sepal lengths and widths and all observed setosa irises.
load fisheriris inds = ~strcmp(species,'setosa'); X = meas(inds,3:4); y = species(inds);
Train an SVM classifier using the processed data set.
SVMModel = ClassificationSVM ResponseName: 'Y' CategoricalPredictors: [] ClassNames: {'versicolor' 'virginica'} ScoreTransform: 'none' NumObservations: 100 Alpha: [24×1 double] Bias: -14.4149 KernelParameters: [1×1 struct] BoxConstraints: [100×1 double] ConvergenceInfo: [1×1 struct] IsSupportVector: [100×1 logical] Solver: 'SMO'
Properties, Methods
SVMModel is a trained ClassificationSVM classifier. Display the properties of SVMModel. For example, to determine the class order, use dot notation.
classOrder = SVMModel.ClassNames
classOrder = 2×1 cell {'versicolor'} {'virginica' }
The first class ('versicolor') is the negative class, and the second ('virginica') is the positive class. You can change the class order during training by using the 'ClassNames' name-value pair argument.
Plot a scatter diagram of the data and circle the support vectors.
sv = SVMModel.SupportVectors; figure gscatter(X(:,1),X(:,2),y) hold on plot(sv(:,1),sv(:,2),'ko','MarkerSize',10) legend('versicolor','virginica','Support Vector') hold off
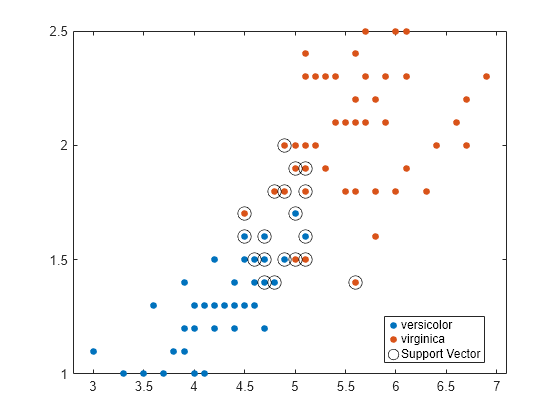
The support vectors are observations that occur on or beyond their estimated class boundaries.
You can adjust the boundaries (and, therefore, the number of support vectors) by setting a box constraint during training using the 'BoxConstraint' name-value pair argument.
Load the ionosphere data set.
Train and cross-validate an SVM classifier. Standardize the predictor data and specify the order of the classes.
rng(1); % For reproducibility CVSVMModel = fitcsvm(X,Y,'Standardize',true,... 'ClassNames',{'b','g'},'CrossVal','on')
CVSVMModel = ClassificationPartitionedModel CrossValidatedModel: 'SVM' PredictorNames: {'x1' 'x2' 'x3' 'x4' 'x5' 'x6' 'x7' 'x8' 'x9' 'x10' 'x11' 'x12' 'x13' 'x14' 'x15' 'x16' 'x17' 'x18' 'x19' 'x20' 'x21' 'x22' 'x23' 'x24' 'x25' 'x26' 'x27' 'x28' 'x29' 'x30' 'x31' 'x32' 'x33' 'x34'} ResponseName: 'Y' NumObservations: 351 KFold: 10 Partition: [1×1 cvpartition] ClassNames: {'b' 'g'} ScoreTransform: 'none'
Properties, Methods
CVSVMModel is a ClassificationPartitionedModel cross-validated SVM classifier. By default, the software implements 10-fold cross-validation.
Alternatively, you can cross-validate a trained ClassificationSVM classifier by passing it to crossval.
Inspect one of the trained folds using dot notation.
ans = CompactClassificationSVM ResponseName: 'Y' CategoricalPredictors: [] ClassNames: {'b' 'g'} ScoreTransform: 'none' Alpha: [78×1 double] Bias: -0.2210 KernelParameters: [1×1 struct] Mu: [0.8888 0 0.6320 0.0406 0.5931 0.1205 0.5361 0.1286 0.5083 0.1879 0.4779 0.1567 0.3924 0.0875 0.3360 0.0789 0.3839 9.6066e-05 0.3562 -0.0308 0.3398 -0.0073 0.3590 -0.0628 0.4064 -0.0664 0.5535 -0.0749 0.3835 … ] (1×34 double) Sigma: [0.3149 0 0.5033 0.4441 0.5255 0.4663 0.4987 0.5205 0.5040 0.4780 0.5649 0.4896 0.6293 0.4924 0.6606 0.4535 0.6133 0.4878 0.6250 0.5140 0.6075 0.5150 0.6068 0.5222 0.5729 0.5103 0.5061 0.5478 0.5712 0.5032 … ] (1×34 double) SupportVectors: [78×34 double] SupportVectorLabels: [78×1 double]
Properties, Methods
Each fold is a CompactClassificationSVM classifier trained on 90% of the data.
Estimate the generalization error.
genError = kfoldLoss(CVSVMModel)
On average, the generalization error is approximately 12%.
More About
A box constraint is a parameter that controls the maximum penalty imposed on margin-violating observations, which helps to prevent overfitting (regularization).
If you increase the box constraint, then the SVM classifier assigns fewer support vectors. However, increasing the box constraint can lead to longer training times.
The Gram matrix of a set of n vectors {_x_1,..,xn; xj ∊ Rp} is an _n_-by-n matrix with element (j,k) defined as G(xj,xk) = <_ϕ_(_xj_),_ϕ_(_xk_)>, an inner product of the transformed predictors using the kernel function ϕ.
For nonlinear SVM, the algorithm forms a Gram matrix using the rows of the predictor data_X_. The dual formalization replaces the inner product of the observations in X with corresponding elements of the resulting Gram matrix (called the “kernel trick”). Consequently, nonlinear SVM operates in the transformed predictor space to find a separating hyperplane.
KKT complementarity conditions are optimization constraints required for optimal nonlinear programming solutions.
In SVM, the KKT complementarity conditions are
for all j = 1,...,n, where f(xj)=ϕ(xj)′β+b, ϕ is a kernel function (see Gram matrix), and ξj is a slack variable. If the classes are perfectly separable, then ξj = 0 for all j = 1,...,n.
One-class learning, or unsupervised SVM, aims to separate data from the origin in the high-dimensional predictor space (not the original predictor space), and is an algorithm used for outlier detection.
The algorithm resembles that of SVM for binary classification. The objective is to minimize the dual expression
with respect to α1,...,αn, subject to
and 0≤αj≤1 for all j = 1,...,n. The value of_G_(xj,xk) is in element (j,k) of the Gram matrix.
A small value of ν leads to fewer support vectors and, therefore, a smooth, crude decision boundary. A large value of ν leads to more support vectors and, therefore, a curvy, flexible decision boundary. The optimal value of_ν_ should be large enough to capture the data complexity and small enough to avoid overtraining. Also, 0 < ν ≤ 1.
For more details, see [4].
Support vectors are observations corresponding to strictly positive estimates of _α_1,...,αn.
SVM classifiers that yield fewer support vectors for a given training set are preferred.
The SVM binary classification algorithm searches for an optimal hyperplane that separates the data into two classes. For separable classes, the optimal hyperplane maximizes a margin (space that does not contain any observations) surrounding itself, which creates boundaries for the positive and negative classes. For inseparable classes, the objective is the same, but the algorithm imposes a penalty on the length of the margin for every observation that is on the wrong side of its class boundary.
The linear SVM score function is
where:
- x is an observation (corresponding to a row of
X). - The vector β contains the coefficients that define an orthogonal vector to the hyperplane (corresponding to
Mdl.Beta). For separable data, the optimal margin length is 2/‖β‖. - b is the bias term (corresponding to
Mdl.Bias).
The root of f(x) for particular coefficients defines a hyperplane. For a particular hyperplane, f(z) is the distance from point z to the hyperplane.
The algorithm searches for the maximum margin length, while keeping observations in the positive (y = 1) and negative (y = –1) classes separate.
- For separable classes, the objective is to minimize ‖β‖ with respect to the β and_b_ subject to_yj_ f(xj) ≥ 1, for all j = 1,..,n. This is the_primal_ formalization for separable classes.
- For inseparable classes, the algorithm uses slack variables (ξj) to penalize the objective function for observations that cross the margin boundary for their class.ξj = 0 for observations that do not cross the margin boundary for their class, otherwise_ξj_ ≥ 0.
The objective is to minimize 0.5‖β‖2+C∑ξj with respect to the β,b, and ξj subject to yjf(xj)≥1−ξj and ξj≥0 for all j = 1,..,n, and for a positive scalar box constraint C. This is the primal formalization for inseparable classes.
The algorithm uses the Lagrange multipliers method to optimize the objective, which introduces_n_ coefficients_α_1,...,αn (corresponding to Mdl.Alpha). The dual formalizations for linear SVM are as follows:
- For separable classes, minimize
with respect to_α_1,...,αn, subject to ∑αjyj=0, αj ≥ 0 for all_j_ = 1,...,n, and Karush-Kuhn-Tucker (KKT) complementarity conditions. - For inseparable classes, the objective is the same as for separable classes, except for the additional condition 0≤αj≤C for all j = 1,..,n.
The resulting score function is
b^ is the estimate of the bias and α^j is the _j_th estimate of the vector α^, j = 1,...,n. Written this way, the score function is free of the estimate of β as a result of the primal formalization.
The SVM algorithm classifies a new observation z using sign(f^(z)).
In some cases, a nonlinear boundary separates the classes. Nonlinear SVM works in a transformed predictor space to find an optimal, separating hyperplane.
The dual formalization for nonlinear SVM is
with respect to_α_1,...,αn, subject to ∑αjyj=0, 0≤αj≤C for all j = 1,..,n, and the KKT complementarity conditions.G(xk,xj) are elements of the Gram matrix. The resulting score function is
For more details, see Understanding Support Vector Machines, [3], and [1].
Algorithms
- For the mathematical formulation of the SVM binary classification algorithm, see Support Vector Machines for Binary Classification and Understanding Support Vector Machines.
NaN,<undefined>, empty character vector (''), empty string (""), and<missing>values indicate missing values.fitcsvmremoves entire rows of data corresponding to a missing response. When computing total weights (see the next bullets),fitcsvmignores any weight corresponding to an observation with at least one missing predictor. This action can lead to unbalanced prior probabilities in balanced-class problems. Consequently, observation box constraints might not equalBoxConstraint.- If you specify the
Cost,Prior, andWeightsname-value arguments, the output model object stores the specified values in theCost,Prior, andWproperties, respectively. TheCostproperty stores the user-specified cost matrix (C) without modification. ThePriorandWproperties store the prior probabilities and observation weights, respectively, after normalization. For model training, the software updates the prior probabilities and observation weights to incorporate the penalties described in the cost matrix. For details, see Misclassification Cost Matrix, Prior Probabilities, and Observation Weights.
Note that theCostandPriorname-value arguments are used for two-class learning. For one-class learning, theCostandPriorproperties store0and1, respectively. - For two-class learning,
fitcsvmassigns a box constraint to each observation in the training data. The formula for the box constraint of observation_j_ is
where C_0 is the initial box constraint (see the BoxConstraint name-value argument), and_wj* is the observation weight adjusted byCostandPriorfor observation j. For details about the observation weights, seeAdjust Prior Probabilities and Observation Weights for Misclassification Cost Matrix. - If you specify Standardize as
trueand set theCost,Prior, orWeightsname-value argument, thenfitcsvmstandardizes the predictors using their corresponding weighted means and weighted standard deviations. That is,fitcsvmstandardizes predictor j (xj) using
where xjk is observation_k_ (row) of predictor j (column), and - Assume that
pis the proportion of outliers that you expect in the training data, and that you set'OutlierFraction',p.- For one-class learning, the software trains the bias term such that 100
p% of the observations in the training data have negative scores. - The software implements robust learning for two-class learning. In other words, the software attempts to remove 100
p% of the observations when the optimization algorithm converges. The removed observations correspond to gradients that are large in magnitude.
- For one-class learning, the software trains the bias term such that 100
- If your predictor data contains categorical variables, then the software generally uses full dummy encoding for these variables. The software creates one dummy variable for each level of each categorical variable.
- The
PredictorNamesproperty stores one element for each of the original predictor variable names. For example, assume that there are three predictors, one of which is a categorical variable with three levels. ThenPredictorNamesis a 1-by-3 cell array of character vectors containing the original names of the predictor variables. - The
ExpandedPredictorNamesproperty stores one element for each of the predictor variables, including the dummy variables. For example, assume that there are three predictors, one of which is a categorical variable with three levels. ThenExpandedPredictorNamesis a 1-by-5 cell array of character vectors containing the names of the predictor variables and the new dummy variables. - Similarly, the
Betaproperty stores one beta coefficient for each predictor, including the dummy variables. - The
SupportVectorsproperty stores the predictor values for the support vectors, including the dummy variables. For example, assume that there are m support vectors and three predictors, one of which is a categorical variable with three levels. ThenSupportVectorsis an _n_-by-5 matrix. - The
Xproperty stores the training data as originally input and does not include the dummy variables. When the input is a table,Xcontains only the columns used as predictors.
- The
- For predictors specified in a table, if any of the variables contain ordered (ordinal) categories, the software uses ordinal encoding for these variables.
- For a variable with k ordered levels, the software creates k – 1 dummy variables. The _j_th dummy variable is –1 for levels up to j, and +1 for levels j + 1 through k.
- The names of the dummy variables stored in the
ExpandedPredictorNamesproperty indicate the first level with the value +1. The software stores k – 1 additional predictor names for the dummy variables, including the names of levels 2, 3, ..., k.
- All solvers implement _L_1 soft-margin minimization.
- For one-class learning, the software estimates the Lagrange multipliers, _α_1,...,αn, such that
References
[1] Hastie, T., R. Tibshirani, and J. Friedman.The Elements of Statistical Learning, Second Edition. NY: Springer, 2008.
[2] Scholkopf, B., J. C. Platt, J. C. Shawe-Taylor, A. J. Smola, and R. C. Williamson. “Estimating the Support of a High-Dimensional Distribution.”Neural Comput., Vol. 13, Number 7, 2001, pp. 1443–1471.
[3] Christianini, N., and J. C. Shawe-Taylor.An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods. Cambridge, UK: Cambridge University Press, 2000.
[4] Scholkopf, B., J. C. Platt, J. C. Shawe-Taylor, A. J. Smola, and R. C. Williamson. “Estimating the Support of a High-Dimensional Distribution.” Neural Comput., Vol. 13, Number 7, 2001, pp. 1443–1471.
[5] Scholkopf, B., and A. Smola. Learning with Kernels: Support Vector Machines, Regularization, Optimization and Beyond, Adaptive Computation and Machine Learning. Cambridge, MA: The MIT Press, 2002.
Extended Capabilities
Usage notes and limitations:
- The predict and update functions support code generation.
- To integrate the prediction of an SVM classification model into Simulink®, you can use the ClassificationSVM Predict block in the Statistics and Machine Learning Toolbox™ library or a MATLAB Function block with the
predictfunction. - When you train an SVM model by using fitcsvm, the following restrictions apply.
- The value of the 'ScoreTransform' name-value pair argument cannot be an anonymous function. For generating code that predicts posterior probabilities given new observations, pass a trained SVM model tofitPosterior or fitSVMPosterior. TheScoreTransform property of the returned model contains an anonymous function that represents the score-to-posterior-probability function and is configured for code generation.
- For fixed-point code generation, the value of the 'ScoreTransform' name-value pair argument cannot be
'invlogit'. Also, the value of the 'KernelFunction' name-value pair argument must be'gaussian','linear', or'polynomial'. - For fixed-point code generation and code generation with a coder configurer, the following additional restrictions apply.
* Categorical predictors (logical,categorical,char,string, orcell) are not supported. You cannot use theCategoricalPredictorsname-value argument. To include categorical predictors in a model, preprocess them by using dummyvar before fitting the model.
* Class labels with thecategoricaldata type are not supported. Both the class label value in the training data (TblorY) and the value of theClassNamesname-value argument cannot be an array with thecategoricaldata type.
For more information, see Introduction to Code Generation.
Usage notes and limitations:
- The following object functions fully support GPU arrays:
- The following object functions offer limited support for GPU arrays:
- The object functions execute on a GPU if at least one of the following applies:
- The model was fitted with GPU arrays.
- The predictor data that you pass to the object function is a GPU array.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2014a
Starting in R2023b, training observations with missing predictor values are included in the X, Y, and W data properties. The RowsUsed property indicates the training observations stored in the model, rather than those used for training. Observations with missing predictor values continue to be omitted from the model training process.
In previous releases, the software omitted training observations that contained missing predictor values from the data properties of the model.
Starting in R2022a, the Cost property stores the user-specified cost matrix, so that you can compute the observed misclassification cost using the specified cost value. The software stores normalized prior probabilities (Prior) and observation weights (W) that do not reflect the penalties described in the cost matrix. To compute the observed misclassification cost, specify theLossFun name-value argument as "classifcost" when you call the loss or resubLoss function.
Note that model training has not changed and, therefore, the decision boundaries between classes have not changed.
For training, the fitting function updates the specified prior probabilities by incorporating the penalties described in the specified cost matrix, and then normalizes the prior probabilities and observation weights. This behavior has not changed. In previous releases, the software stored the default cost matrix in the Cost property and stored the prior probabilities and observation weights used for training in thePrior and W properties, respectively. Starting in R2022a, the software stores the user-specified cost matrix without modification, and stores normalized prior probabilities and observation weights that do not reflect the cost penalties. For more details, see Misclassification Cost Matrix, Prior Probabilities, and Observation Weights.
Some object functions use the Cost, Prior, and W properties:
- The
lossandresubLossfunctions use the cost matrix stored in theCostproperty if you specify theLossFunname-value argument as"classifcost"or"mincost". - The
lossandedgefunctions use the prior probabilities stored in thePriorproperty to normalize the observation weights of the input data. - The
resubLossandresubEdgefunctions use the observation weights stored in theWproperty.
If you specify a nondefault cost matrix when you train a classification model, the object functions return a different value compared to previous releases.
If you want the software to handle the cost matrix, prior probabilities, and observation weights in the same way as in previous releases, adjust the prior probabilities and observation weights for the nondefault cost matrix, as described in Adjust Prior Probabilities and Observation Weights for Misclassification Cost Matrix. Then, when you train a classification model, specify the adjusted prior probabilities and observation weights by using the Prior and Weights name-value arguments, respectively, and use the default cost matrix.