resubMargin - Resubstitution classification margin - MATLAB (original) (raw)
Resubstitution classification margin
Syntax
Description
`m` = resubMargin([Mdl](#mw%5F78d4a3b9-0333-4fcc-9b1b-4c24c6c1b4de%5Fsep%5Fshared-Mdl)) returns the resubstitution Classification Margin (m) for the trained classification model Mdl using the predictor data stored inMdl.X and the corresponding true class labels stored inMdl.Y.
m is returned as an _n_-by-1 numeric column vector, where n is the number of observations in the predictor data.
`m` = resubMargin([Mdl](#mw%5F78d4a3b9-0333-4fcc-9b1b-4c24c6c1b4de%5Fsep%5Fshared-Mdl),'IncludeInteractions',[includeInteractions](#mw%5F0060803c-69fc-4975-88ec-7097c4c8fded)) specifies whether to include interaction terms in computations. This syntax applies only to generalized additive models.
Examples
Estimate the resubstitution (in-sample) classification margins of a naive Bayes classifier. An observation margin is the observed true class score minus the maximum false class score among all scores in the respective class.
Load the fisheriris data set. Create X as a numeric matrix that contains four measurements for 150 irises. Create Y as a cell array of character vectors that contains the corresponding iris species.
load fisheriris X = meas; Y = species;
Train a naive Bayes classifier using the predictors X and class labels Y. A recommended practice is to specify the class names. fitcnb assumes that each predictor is conditionally and normally distributed.
Mdl = fitcnb(X,Y,'ClassNames',{'setosa','versicolor','virginica'})
Mdl = ClassificationNaiveBayes ResponseName: 'Y' CategoricalPredictors: [] ClassNames: {'setosa' 'versicolor' 'virginica'} ScoreTransform: 'none' NumObservations: 150 DistributionNames: {'normal' 'normal' 'normal' 'normal'} DistributionParameters: {3×4 cell}
Properties, Methods
Mdl is a trained ClassificationNaiveBayes classifier.
Estimate the resubstitution classification margins.
m = resubMargin(Mdl); median(m)
Display the histogram of the in-sample classification margins.
histogram(m,30,'Normalization','probability') xlabel('In-Sample Margins') ylabel('Probability') title('Probability Distribution of the In-Sample Margins')
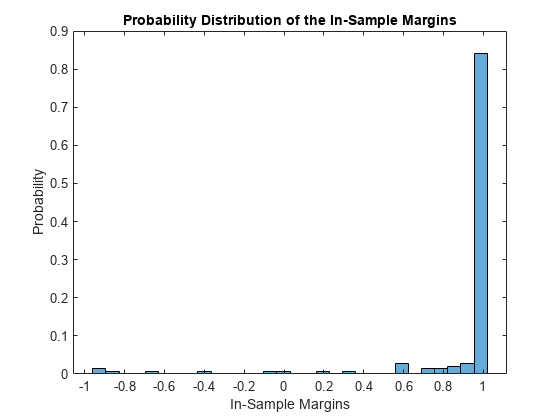
Classifiers that yield relatively large margins are preferred.
Perform feature selection by comparing in-sample margins from multiple models. Based solely on this comparison, the model with the highest margins is the best model.
Load the ionosphere data set. Define two data sets:
fullXcontains all predictors (except the removed column of 0s).partXcontains the last 20 predictors.
load ionosphere fullX = X; partX = X(:,end-20:end);
Train a support vector machine (SVM) classifier for each predictor set.
FullSVMModel = fitcsvm(fullX,Y); PartSVMModel = fitcsvm(partX,Y);
Estimate the in-sample margins for each classifier.
fullMargins = resubMargin(FullSVMModel); partMargins = resubMargin(PartSVMModel); n = size(X,1); p = sum(fullMargins < partMargins)/n
Approximately 22% of the margins from the full model are less than those from the model with fewer predictors. This result suggests that the model trained with all the predictors is better.
Compare a generalized additive model (GAM) with linear terms to a GAM with both linear and interaction terms by examining the training sample margins and edge. Based solely on this comparison, the classifier with the highest margins and edge is the best model.
Load the 1994 census data stored in census1994.mat. The data set consists of demographic data from the US Census Bureau to predict whether an individual makes over $50,000 per year. The classification task is to fit a model that predicts the salary category of people given their age, working class, education level, marital status, race, and so on.
census1994 contains the training data set adultdata and the test data set adulttest. To reduce the running time for this example, subsample 500 training observations from adultdata by using the datasample function.
rng('default') % For reproducibility NumSamples = 5e2; adultdata = datasample(adultdata,NumSamples,'Replace',false);
Train a GAM that contains both linear and interaction terms for predictors. Specify to include all available interaction terms whose _p_-values are not greater than 0.05.
Mdl = fitcgam(adultdata,'salary','Interactions','all','MaxPValue',0.05)
Mdl = ClassificationGAM PredictorNames: {'age' 'workClass' 'fnlwgt' 'education' 'education_num' 'marital_status' 'occupation' 'relationship' 'race' 'sex' 'capital_gain' 'capital_loss' 'hours_per_week' 'native_country'} ResponseName: 'salary' CategoricalPredictors: [2 4 6 7 8 9 10 14] ClassNames: [<=50K >50K] ScoreTransform: 'logit' Intercept: -28.5594 Interactions: [82×2 double] NumObservations: 500
Properties, Methods
Mdl is a ClassificationGAM model object. Mdl includes 82 interaction terms.
Estimate the training sample margins and edge for Mdl.
M = resubMargin(Mdl); E = resubEdge(Mdl)
Estimate the training sample margins and edge for Mdl without including interaction terms.
M_nointeractions = resubMargin(Mdl,'IncludeInteractions',false); E_nointeractions = resubEdge(Mdl,'IncludeInteractions',false)
E_nointeractions = 0.9516
Display the distributions of the margins using box plots.
boxplot([M M_nointeractions],'Labels',{'Linear and Interaction Terms','Linear Terms Only'}) title('Box Plots of Training Sample Margins')
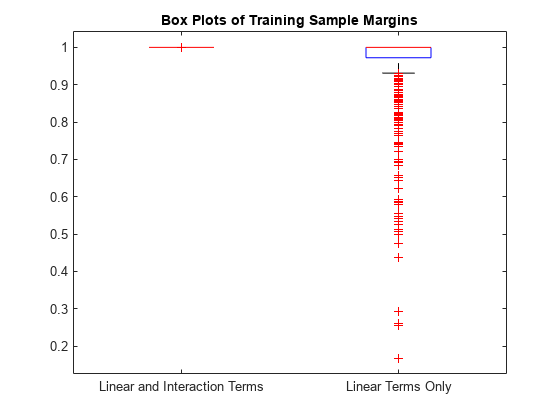
When you include the interaction terms in the computation, all the resubstitution margin values for Mdl are 1, and the resubstitution edge value (average of the margins) is 1. The margins and edge decrease when you do not include the interaction terms in Mdl.
Input Arguments
Flag to include interaction terms of the model, specified as true orfalse. This argument is valid only for a generalized additive model (GAM). That is, you can specify this argument only whenMdl is ClassificationGAM.
The default value is true if Mdl contains interaction terms. The value must be false if the model does not contain interaction terms.
Data Types: logical
More About
The classification margin for binary classification is, for each observation, the difference between the classification score for the true class and the classification score for the false class. The_classification margin_ for multiclass classification is the difference between the classification score for the true class and the maximal classification score for the false classes.
If the margins are on the same scale (that is, the score values are based on the same score transformation), then they serve as a classification confidence measure. Among multiple classifiers, those that yield greater margins are better.
Algorithms
resubMargin computes the classification margin according to the corresponding margin function of the object (Mdl). For a model-specific description, see the margin function reference pages in the following table.
Extended Capabilities
Version History
Introduced in R2012a
Starting in R2023b, the following classification model object functions use observations with missing predictor values as part of resubstitution ("resub") and cross-validation ("kfold") computations for classification edges, losses, margins, and predictions.
In previous releases, the software omitted observations with missing predictor values from the resubstitution and cross-validation computations.