Inferring Human Population Sizes, Divergence Times and Rates of Gene Flow From Mitochondrial, X and Y Chromosome Resequencing Data (original) (raw)
Abstract
We estimate parameters of a general isolation-with-migration model using resequence data from mitochondrial DNA (mtDNA), the Y chromosome, and two loci on the X chromosome in samples of 25–50 individuals from each of 10 human populations. Application of a coalescent-based Markov chain Monte Carlo technique allows simultaneous inference of divergence times, rates of gene flow, as well as changes in effective population size. Results from comparisons between sub-Saharan African and Eurasian populations estimate that 1500 individuals founded the ancestral Eurasian population ∼40 thousand years ago (KYA). Furthermore, these small Eurasian founding populations appear to have grown much more dramatically than either African or Oceanian populations. Analyses of sub-Saharan African populations provide little evidence for a history of population bottlenecks and suggest that they began diverging from one another upward of 50 KYA. We surmise that ancestral African populations had already been geographically structured prior to the founding of ancestral Eurasian populations. African populations are shown to experience low levels of mitochondrial DNA gene flow, but high levels of Y chromosome gene flow. In particular, Y chromosome gene flow appears to be asymmetric, i.e., from the Bantu-speaking population into other African populations. Conversely, mitochondrial gene flow is more extensive between non-African populations, but appears to be absent between European and Asian populations.
THE demographic history of human populations is a matter of fundamental importance for understanding the patterns of genetic variation observed throughout the genome. Demographic processes such as population growth and divergence, as well as gene flow between populations, are the primary factors contributing to the patterns of neutral DNA polymorphism. It is only when these processes can be accurately characterized that identification of genomic regions with anomalous patterns of nucleotide variability can be attributed to natural selection with confidence (Teshima et al. 2006).
A great deal has already been learned about the demographic history of human populations from genomic sequence data (Garrigan and Hammer 2006). For example, a number of studies of neutral DNA polymorphism uncover evidence for a recent, severe population bottleneck in the history of non-African populations (Reich et al. 2001; Marth et al. 2004; Voight et al. 2005). Population bottlenecks are known to reduce genetic variability (Maruyama and Fuerst 1985a,b), while inflating the genetic differences between populations (Hedrick 1999). Yet the existence of a non-African bottleneck has been inferred only through the analysis of separate population samples, an approach that neglects any effects of human population structure. Neglecting population structure and gene flow between populations may be problematic because recent gene flow can mimic the effects of other demographic events, such as changes in effective pop-ulation size (Wakeley and Aliacar 2001). Conversely, a number of other studies draw inferences about population structure without consideration of the effects of population bottlenecks, or other nonequilibrium demographic processes (Jorde et al. 2000; Romualdi et al. 2002; Charlesworth et al. 2003).
There are a handful of studies that simultaneously account for both population structure and nonequilibrium demography (Wakeley et al. 2001; Ray et al. 2003; Ramachandran et al. 2005). However, the biological inferences gleaned from such analyses are dependent upon the population genetic models assumed by the investigators. Some studies assumed an island model of population structure, in which individual populations are allowed to vary in their sizes and rates of migration (Wakeley et al. 2001; Ray et al. 2003). Under the island model, populations share common ancestry only via gene flow due to migration. Other studies assume that populations diverge, undergo bottlenecks, and subsequently remain isolated, experiencing no gene flow from neighboring populations (Prugnolle et al. 2005; Ramachandran et al. 2005). These differing assumptions can lead to alternative conclusions concerning demographic history. For example, the commonly employed statistical summary of population differentiation, _F_ST, has a genomic average value of 0.12 for autosomal single nucleotide polymorphisms between three populations representing Africa, Asia, and Europe (International Hapmap Consortium 2005). Under the island model, the expected 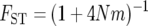 (Wright 1940), so that the inference is that continental human populations exchange an average of 1.83 migrants per generation. Alternatively, under the pure divergence model, the expected
(Wright 1940), so that the inference is that continental human populations exchange an average of 1.83 migrants per generation. Alternatively, under the pure divergence model, the expected 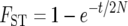 (Nei 1987). Under this model, assuming the human effective population size is N = 10,000, the inference is that populations diverged approximately t = 51 thousand years ago (KYA) and exchanged no migrants after that time (assuming a 20-year generation interval). To account more thoroughly for biological reality, it is desirable to estimate simultaneously both when populations diverged and how much gene flow occurred thereafter.
(Nei 1987). Under this model, assuming the human effective population size is N = 10,000, the inference is that populations diverged approximately t = 51 thousand years ago (KYA) and exchanged no migrants after that time (assuming a 20-year generation interval). To account more thoroughly for biological reality, it is desirable to estimate simultaneously both when populations diverged and how much gene flow occurred thereafter.
The estimation of historical human demographic parameters is also influenced by how DNA sequence polymorphism is measured and analyzed. One example is the choice of loci for inclusion in a study. Often contrasting demographic histories have been inferred for the two sex-specific loci: the mitochondrial DNA (mtDNA) and the nonrecombining Y chromosome (NRY). In many non-African populations, the mtDNA shows the signal of rapid population growth and low levels of differentiation between populations, while the NRY shows a diminished signal of population growth and much higher levels of differentiation (Seielstad et al. 1998; Rogers et al. 2000; Hammer et al. 2003; Wilder et al. 2004). Likewise, the signals of population growth also depend upon how populations are sampled. If a small number of individuals from multiple populations are pooled together in an analysis, one may easily confound population growth with population structure (Ptak and Przeworski 2002; Hammer et al. 2003). Finally, measuring DNA polymorphism by genotyping single nucleotide polymorphisms (SNPs) results in a known ascertainment bias that is minimized by resequencing entire homologous regions from multiple individuals (Nielsen 2004).
The isolation-with-migration (IM) model provides a more general framework for making inferences regarding human demographic history (Nielsen and Wakeley 2001; Hey and Nielsen 2004). This two-population model assumes that populations diverge and subsequently experience gene flow. Additionally, the IM model does not require that rates of gene flow be symmetrical between populations and each population is allowed to change size independently (Hey 2005). In this study, we analyze DNA resequencing data from the mtDNA, Y chromosome, and two X-linked introns from large samples of individuals taken from each of 10 anthropologically defined human populations. Although inference under this general model is still not without its caveats, several consistent results emerge, including severe bottlenecks in the history of non-African populations, widely varying local population sizes and rates of growth, and older divergence between African populations than between non-African populations.
MATERIALS AND METHODS
DNA samples and sequencing:
Nucleotide sequence data were obtained from 10 human populations representing major Old World population centers (Figure 1). Four populations reside in Africa: the Bakola from Cameroon (n = 25), southeastern Bantu-speakers from South Africa (referred to as SE Bantu, n = 50), the Dogon from Mali (n = 45), and San from Namibia (n = 25). Two European populations were sampled: the Dutch (n = 47) and central Italians (n = 56). Two Asian populations were sampled: Mongolians (n = 59) and Sri Lankans (n = 50). Finally, two Oceanian populations were also surveyed: Papua New Guineans (n = 24) and the Baining from New Britain (n = 50). The above values represent maximal sample sizes, which may not have been obtained for all loci (Tables 1 and 2). While all sequences were generated from the same panel of individuals, sample sizes vary slightly between this work and the previously published data (Wilder et al. 2004). All subjects were male to ensure that phased X-linked haplotypes were recovered. All sampling protocols were approved by the Human Subjects Committee at the University of Arizona, and by the regional centers where samples were collected.
Figure 1.—
Map showing the geographical locations of the 10 human populations sampled for DNA resequencing in this study.
TABLE 1.
Summary statistics describing resequencing nucleotide polymorphism (θW and π) and the frequency spectra (Tajima's D, Fu and Li's D*, and Fay and Wu's H) at the mitochondrial COIII locus and the NRY for 10 human populations
| Locus | Population | n | S | L | θW (%) | π (%) | D | D* | H |
|---|---|---|---|---|---|---|---|---|---|
| COIII | Bakola | 25 | 6 | 780 | 0.204 | 0.132 | −1.058 | −0.331 | 0.887 |
| SE Bantu | 50 | 16 | 780 | 0.458 | 0.331 | −0.857 | −1.157 | 1.127 | |
| Dogon | 42 | 5 | 780 | 0.149 | 0.094 | −0.937 | −1.794 | −0.005 | |
| San | 25 | 11 | 780 | 0.373 | 0.273 | −0.906 | −0.046 | −0.580 | |
| Mongolian | 50 | 17 | 780 | 0.487 | 0.201 | −1.831 | −3.290 | 1.140 | |
| Sri Lankan | 50 | 12 | 780 | 0.343 | 0.130 | −1.838 | −3.663 | 0.313 | |
| Dutch | 47 | 13 | 780 | 0.377 | 0.106 | −2.179 | −3.287 | −1.172 | |
| Italian | 56 | 20 | 780 | 0.558 | 0.136 | −2.370 | −4.859 | −0.968 | |
| Baining | 50 | 4 | 780 | 0.114 | 0.147 | 0.651 | −0.122 | 0.584 | |
| Papuan | 24 | 5 | 780 | 0.172 | 0.121 | −0.859 | −1.473 | −0.029 | |
| NRY | Bakola | 25 | 14 | 6673 | 0.056 | 0.060 | 0.286 | 0.317 | 1.360 |
| SE Bantu | 47 | 10 | 6653 | 0.034 | 0.044 | 0.823 | −0.475 | 1.034 | |
| Dogon | 40 | 12 | 6654 | 0.042 | 0.037 | −0.402 | −0.654 | 1.162 | |
| San | 25 | 10 | 6614 | 0.040 | 0.041 | 0.089 | 0.941 | −0.727 | |
| Mongolian | 56 | 8 | 6654 | 0.026 | 0.010 | −1.601 | −1.729 | 0.632 | |
| Sri Lankan | 43 | 7 | 6654 | 0.024 | 0.010 | −1.641 | −3.498 | 0.527 | |
| Dutch | 47 | 3 | 6654 | 0.010 | 0.009 | −0.275 | −1.752 | −0.037 | |
| Italian | 47 | 4 | 6654 | 0.014 | 0.010 | −0.679 | −2.361 | 0.146 | |
| Baining | 48 | 3 | 6651 | 0.010 | 0.020 | 1.993 | 0.899 | 0.644 | |
| Papuan | 24 | 4 | 6651 | 0.016 | 0.006 | −1.690 | −1.991 | 0.384 |
TABLE 2.
Summary statistics describing resequencing nucleotide polymorphism (θW and π), recombination rate (ρ), and the frequency spectra (Tajima's D, Fu and Li's D*, and Fay and Wu's H) at two X-linked introns for 10 human populations
| Locus | Population | n | S | L | θW (%) | π (%) | ρ (%) | D | D* | H |
|---|---|---|---|---|---|---|---|---|---|---|
| APXL | Bakola | 21 | 14 | 4972 | 0.078 | 0.073 | 0.000 | −0.244 | 0.382 | 1.157 |
| SE Bantu | 48 | 29 | 5421 | 0.121 | 0.076 | 0.268 | −1.213 | −1.360 | −0.236 | |
| Dogon | 38 | 18 | 5427 | 0.079 | 0.069 | 0.089 | −0.407 | 0.940 | −0.706 | |
| San | 25 | 15 | 5435 | 0.073 | 0.083 | 0.208 | 0.453 | 1.263 | −2.610 | |
| Mongolian | 59 | 7 | 5411 | 0.028 | 0.031 | 0.000 | 0.334 | 0.424 | 0.234 | |
| Sri Lankan | 47 | 8 | 5431 | 0.033 | 0.038 | 0.014 | 0.420 | −0.885 | −2.609 | |
| Dutch | 43 | 10 | 5426 | 0.043 | 0.056 | 0.000 | 0.929 | 0.198 | −3.394 | |
| Italian | 56 | 9 | 5427 | 0.036 | 0.047 | 0.074 | 0.804 | −0.740 | −0.751 | |
| Baining | 49 | 10 | 5422 | 0.041 | 0.038 | 0.041 | −0.245 | −2.445 | 0.602 | |
| Papuan | 19 | 7 | 5437 | 0.037 | 0.061 | 0.000 | 2.198 | 1.385 | 0.310 | |
| DMD44 | Bakola | 23 | 13 | 2969 | 0.119 | 0.105 | 0.227 | −0.398 | 0.706 | −0.300 |
| SE Bantu | 50 | 20 | 3003 | 0.149 | 0.149 | 2.708 | −0.001 | −0.218 | 0.395 | |
| Dogon | 45 | 14 | 3009 | 0.106 | 0.136 | 1.623 | 0.872 | 0.615 | −0.826 | |
| San | 25 | 11 | 2989 | 0.097 | 0.114 | 0.950 | 0.561 | 1.021 | −2.367 | |
| Mongolian | 50 | 12 | 3011 | 0.089 | 0.099 | 0.586 | 0.334 | −0.766 | −1.058 | |
| Sri Lankan | 47 | 11 | 3007 | 0.083 | 0.111 | 0.128 | 0.999 | 0.298 | 1.063 | |
| Dutch | 44 | 13 | 2988 | 0.100 | 0.104 | 0.152 | 0.119 | 0.006 | −0.628 | |
| Italian | 52 | 14 | 3007 | 0.103 | 0.128 | 0.625 | 0.732 | 1.105 | −2.103 | |
| Baining | 50 | 10 | 3009 | 0.074 | 0.119 | 0.516 | 1.733 | 1.458 | −1.319 | |
| Papuan | 24 | 7 | 2989 | 0.063 | 0.050 | 0.145 | −0.612 | 1.355 | −6.377 |
Four loci were resequenced, including two sex-specific haploid loci and two X-linked introns. The haploid data consist of 780 bp of the cytochrome oxidase subunit III (COIII) gene from the mitochondrial genome and 6650 bp encompassing 13 Alu elements on the Y chromosome (NRY). Both the COIII and NRY data sets have been previously published (Wilder et al. 2004). We chose the 13 Y chromosome regions because they were shown to have a threefold higher SNP density than other Y chromosome noncoding regions, and the COIII gene because it demonstrates considerably less homoplasy than the D-loop (Wilder et al. 2004). The X-linked sequences consist of 5441 bp of the apical-like Xenopus laevis (APXL) intron 4 and 3045 bp of the Duchenne muscular dystrophy intron 44 (DMD44). For the two X-linked introns, a single male common chimpanzee (Pan troglodytes) was also sequenced from DNA samples provided by O. Ryder. Both the amplification and sequencing primers are available from the authors upon request. Overlapping sequence fragments were assembled and aligned with the computer application Sequencher, version 4 (GeneCodes, Ann Arbor, MI).
Summary statistics and mutation rates:
Features of the sequence alignments for each locus and each population can be described by a battery of summary statistics. Levels of nucleotide polymorphism are summarized by two quantities that are moment estimators of the population mutation rate (θ = 4_N_μ for an autosomal locus, where μ is the neutral rate of mutation) under the assumptions of the standard neutral model. The unbiased estimator of Watterson (1975), θW, is calculated from the number of segregating sites (S) and summarizes the total length of ancestral coalescent genealogies. The estimator of Tajima (1983), π, is the average number of pairwise nucleotide differences and summarizes the average coalescence time. The population recombination rate (ρ = 2_Nc_ for an X-linked locus, where c is the rate of crossing over) was also estimated from the X-linked intron polymorphism data by the method of McVean et al. (2002). Differences in the mean values of θW and ρ, across all four loci, between African and non-African populations were tested for statistical significance with Hotelling's _T_2 statistic, which is a multivariate generalization of Student's t statistic. Finally, the polymorphism frequency distribution was summarized with three complementary statistics. The statistic D is based on the normalized difference θW − π (Tajima 1989), D* summarizes the number of singletons (Fu and Li 1993), and H is the difference between π and an estimator of θ weighted by the frequency of derived polymorphisms (Fay and Wu 2000). The probabilities of the observed summaries of the polymorphism frequency spectra under the standard neutral model were obtained via coalescent simulation using the program ms (http://home.uchicago.edu/∼rhudson1/source/mksamples.html). In each case, the simulated samples had the same number of segregating sites as the actual sample and the rate of crossing over was taken from the estimates of ρ described above.
Mutation rates for each locus were estimated for the purposes of converting scaled parameter estimates into demographic estimates. For the two haploid loci, the COIII and NRY mutation rates were taken from Wilder et al. (2004). For the two X-linked introns, the net pairwise sequence difference with the chimpanzee outgroup (Nei 1987) was calculated and then divided by twice the assumed human–chimpanzee divergence of six million years to obtain the per year estimate of the neutral nucleotide substitution rate. For all calculations involving quantities measured in units of generations, the human generation time is assumed to be 20 years.
Isolation-with-migration model:
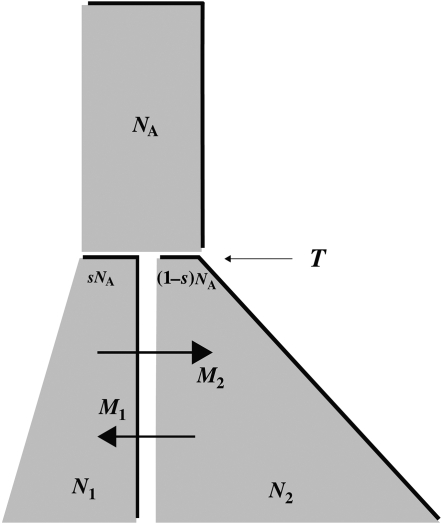
There are seven basic parameters in the two-population IM model: the current effective size of the two populations (_N_C1 and _N_C2), the ancestral effective population size (_N_A), the number of generations since the populations split (T), the proportion of _N_A that founded population 1 (s), the rate of gene flow into population 1 (_M_1) and the rate of gene flow into population 2 (_M_2) (Figure 2). All parameters, besides s, can be scaled by the neutral mutation rate μ by setting (as an autosomal example) θ1 = 4_N_C1μ, θ2 = 4_N_C2μ, θA = 4_N_Aμ, t = _T_μ, _m_1 = _M_1/μ and _m_2 = _M_2/μ. A vector of all parameters that are free to vary is collectively denoted by λ = {θ1, θ2, θA, t, s, _m_1, m_2}. The IM model allows the two descendant populations to change size exponentially over the course of T generations, such that 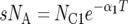 or
or 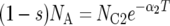 , where α_i is the intrinsic rate of exponential growth per generation for population i. Finally, it is important to note that the IM model does not take into account the effects of either natural selection or intragenic recombination.
, where α_i is the intrinsic rate of exponential growth per generation for population i. Finally, it is important to note that the IM model does not take into account the effects of either natural selection or intragenic recombination.
Figure 2.—
A schematic of the isolation-with-migration (IM) model. The IM model includes two populations that diverge from one another at time T from a common ancestral population of size _N_A. After time T, the ancestral population splits into two daughter populations, one of size _sN_A and the other of size (1 − s)_N_A. The populations are allowed to grow (or shrink) exponentially until the current generation. Over the course of these T generations, gene flow can occur between the two populations and can occur at different rates in each direction.
Parameter estimation:
Inferences regarding the set of parameters in the IM model (λ) can be made from multilocus DNA polymorphism data using a Markov chain Monte Carlo (MCMC) technique (Nielsen and Wakeley 2001; Hey and Nielsen 2004). By specifying a prior probability distribution for λ, a Bayesian approach can be taken to approximating the posterior probability distribution of parameters, given a nonrecombining DNA polymorphism data set at the _i_th of l sampled loci (Xi):
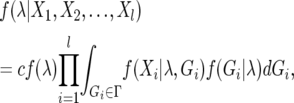
where Gi is a genealogical history at the _i_th locus with sample space Γ, c is a constant that ensures the posterior probability sums to unity, and f (λ) is the prior probability distribution of parameters λ, which is assumed to be uniform along some specified interval. This integral can be evaluated using Monte Carlo simulation of the coalescent process, where f (Gi | λ) is the joint density function for both coalescence and migration events (Beerli and Felsenstein 1999). Under the infinite sites model of mutation, f (Xi | λ, Gi) can be calculated by mapping mutations in Xi onto the simulated genealogy, Gi. However, most genealogies sampled from Γ are expected to contribute little to the overall likelihood, therefore genealogical sampling efficiency is improved with a proposal algorithm for updates in Gi that is similar to the “conditional coalescent” proposal algorithm of Beerli and Felsenstein (1999).
A Markov chain describing (λ, Gi) can be constructed with stationary distribution 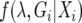 . The posterior distribution of λ is estimated by sampling from the chain at stationarity (i.e., after an initial “burn-in” period of 105 steps). Updates in the chain are accepted according to a Metropolis–Hastings criterion given by Nielsen and Wakeley (2001). Different parameters in λ may be updated at different rates, the t parameter updates especially slowly, which may cause the chain to converge to an incorrect stationary distribution. Multiple Metropolis-coupled Markov chains were run simultaneously to improve the mixing of parameters. The swapping of parameters between Metropolis-coupled chains was governed by a two-step scheme, at each step the heating term (β) for the _i_th chain,
. The posterior distribution of λ is estimated by sampling from the chain at stationarity (i.e., after an initial “burn-in” period of 105 steps). Updates in the chain are accepted according to a Metropolis–Hastings criterion given by Nielsen and Wakeley (2001). Different parameters in λ may be updated at different rates, the t parameter updates especially slowly, which may cause the chain to converge to an incorrect stationary distribution. Multiple Metropolis-coupled Markov chains were run simultaneously to improve the mixing of parameters. The swapping of parameters between Metropolis-coupled chains was governed by a two-step scheme, at each step the heating term (β) for the _i_th chain, 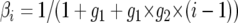 , and we elected to have _g_1 = 0.05 and _g_2 = 2. Overall mixing of the unheated chain was assessed both through the observed autocorrelation of parameters in λ and through its updated acceptance rates.
, and we elected to have _g_1 = 0.05 and _g_2 = 2. Overall mixing of the unheated chain was assessed both through the observed autocorrelation of parameters in λ and through its updated acceptance rates.
The IM program (http://lifesci.rutgers.edu∼heylab/HeylabSoftware.htm#IM) was run on all data sets for 10 million steps of a single chain with the following bounded uniform priors: 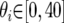 ;
; 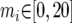 for i = 1, 2;
for i = 1, 2; 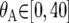 ;
; 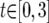 ;
; 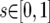 . If these ranges did not contain the full marginal posterior probability density, the upper bound was increased incrementally. Once plausible ranges were found, up to eight Metropolis-coupled chains of 10 million steps were run. The number of chains was determined by how well the t parameter mixed in the initial runs. If >15% of proposed updates to t were accepted, a minimum of three chains was always run. Additional runs were performed in which each of the four loci was allowed to experience independent rates of gene flow.
. If these ranges did not contain the full marginal posterior probability density, the upper bound was increased incrementally. Once plausible ranges were found, up to eight Metropolis-coupled chains of 10 million steps were run. The number of chains was determined by how well the t parameter mixed in the initial runs. If >15% of proposed updates to t were accepted, a minimum of three chains was always run. Additional runs were performed in which each of the four loci was allowed to experience independent rates of gene flow.
In some cases, the data had to be modified to fit the assumptions of the IM model, specifically that mutations occur according to an infinite-sites model and that there is no intragenic recombination. The four-gamete test was applied to all two-population polymorphism data sets to test compatibility with these two assumptions (Hudson and Kaplan 1985). If polymorphic sites in the nonrecombining haploid data sets were found to have pairs with all four gametic types, back mutation was assumed to be responsible and a finite-sites model of mutation was used (Hasegawa et al. 1985). X-linked sites with all four gametic types were assumed to be the result of recombination events and were subsequently eliminated from the data set in one of two ways. If only a small number of haplotypes were recombinants (i.e., one or two), those haplotypes were excluded from the analysis. If more than two haplotypes were recombinants, the minimum number of incongruent sites was eliminated such that the data fit the infinite-sites model of mutation. The most sites eliminated by this latter criterion were 5 of 17 polymorphic DMD44 sites in the SE Bantu–Dogon comparison. The IM input files are available from the Hammer lab website (http://hammerlab.biosci.arizona.edu/publications/supplementary_data/XPOP_DATA.zip).
Due to the heavy computational burden of analyzing all 45 pairwise combinations of the 10 populations, analysis was carried out on only a subset of possible comparisons. Thirteen pairs of populations were chosen on the basis of geography. Finally, to check the convergence of all chains to the correct stationary distribution, a minimum of three independent replicates was performed and all reported maximum-likelihood parameter estimates represent the mean of these replicate runs of the IM program. The command lines used for IM program are provided in supplemental Table S1 at http://www.genetics.org/supplemental/.
RESULTS
A total of 16.2 kb of resequencing data from the mtDNA, Y, and X chromosomes were obtained from >400 individuals sampled from 10 human populations. Total levels of multilocus DNA polymorphism are significantly higher in African than non-African populations (Hotelling's _T_2 = 85.70; P = 0.004): non-African populations have 26% of the level of African NRY diversity, 38% of the African COIII diversity, 61% at APXL, and 91% at DMD44 (Tables 1 and 2). African X-linked sequences are also estimated to have greater population recombination rates (Table 2), although this difference is not statistically significant (T 2 = 6.43; P = 0.127). Estimated population recombination rates are nearly an order of magnitude higher, on average, for the DMD44 locus compared with the APXL locus. The population mutation and recombination rates are significantly correlated among the 10 populations for both APXL (r = 0.779; P = 0.008) and DMD44 (r = 0.734; P = 0.016).
Summary statistics describing the polymorphism frequency spectra can provide preliminary insights into which loci are most impacted by deviations from mutation-drift equilibrium (Tables 1 and 2). For example, negative values of Tajima's D statistic at the COIII locus indicate an excess of low frequency polymorphisms over that expected under mutation-drift equilibrium (the standard neutral model). Coalescent simulations of the standard neutral model indicate that this excess is significant in several non-African populations: Mongolians (P = 0.013), Sri Lankans (P = 0.011), Dutch (P = 0.001), and Italians (P < 0.001). The NRY locus shows a significant excess of low frequency polymorphisms only for the Mongolians (P = 0.032), Sri Lankans (P = 0.031), and Papuans (P = 0.019), while the Baining show a significant deficit of low frequency polymorphisms (P = 0.033). The X-linked introns also show a significant deficit of low frequency polymorphisms at APXL in the San (D* = 1.263; P = 0.032), the Papuans (P = 0.008), and in the Baining at DMD44 (P = 0.036). The Papuans also have a significant excess of high frequency derived polymorphism at DMD44 (H = −6.377; P = 0.004). Finally, the neutral mutation rates per locus per year were estimated as 1.23 × 10−5 for COIII, 8.88 × 10−6 for NRY, 6.02 × 10−6 for APXL, and 2.27 × 10−6 for DMD44.
MCMC convergence and diagnostics:
For each two-population data set, from which IM parameters were estimated, four independent replicates of Metropolis-coupled Markov chains were run. Convergence of the unheated Markov chains to their true stationary distributions were verified by examining whether each replicate independently converges to similar parameter values and whether the model parameters within each of the four replicates mixes well. The resulting marginal posterior probability distributions for the thirteen pairwise population comparisons are included as supplemental Figures S1–S13 at http://www.genetics.org/supplemental/. In almost all cases, each of the four replicates yields a posterior distribution with identical modes. The most troubling instances of failure to converge involve θA, the ancestral effective population size parameter. For the SE Bantu–Bakola, SE Bantu–Dogon, and Dutch–Italian comparisons, independent replicates did not result in identical modes of the posterior distributions (supplemental Figures S3, S4, and S13 at http://www.genetics.org/supplemental/).
There are also several instances of diffuse marginal posterior probability distributions. A diffuse posterior distribution is relatively flat and lacks a well-defined mode. In 5 of 13 comparisons, the current effective population size parameter (_N_C) for non-African populations has diffuse marginal posteriors. Likewise, the splitting time parameters (t) for the Dogon–San and Bakola–San comparisons also have diffuse posterior distributions (Figure 3). Finally, the migration parameters in the Dutch–Italian comparison are also characterized by diffuse posteriors (supplemental Figure S13 at http://www.genetics.org/supplemental/). In each of the above mentioned cases, the parameter estimates were very large relative to those of other data sets. This undesirable property of the posterior distributions is likely to be the result of a lack of information in the data.
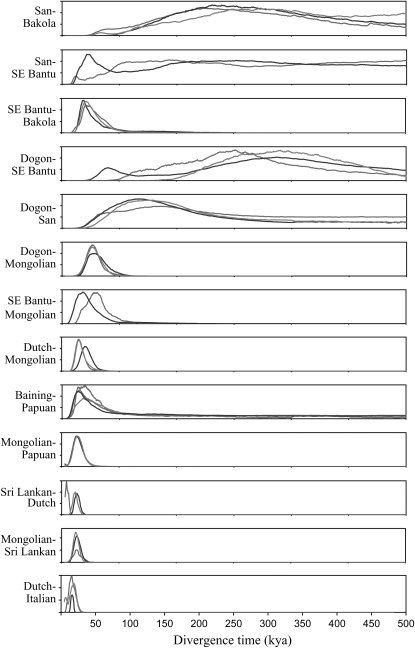
Figure 3.—
Posterior probability distributions for the divergence time parameter in the IM model in 13 pairwise population comparisons. Each curve represents an independent run of the MCMC algorithm. The timescale shown at the bottom is in thousands of years before the present.
For posterior distributions that do appear to sample from stationary distributions, it is important to check whether the chains mixed adequately, thereby providing reassurance that the chains did not converge to the wrong stationary distribution (i.e., local maxima). The effective sample size (ESS) and update acceptance rates (R) for the unheated chain are provided in supplemental Table S2 at http://www.genetics.org/supplemental/. The θA, t, and s parameters consistently show both R < 10% and ESS < 50. However, in each instance of poor mixing behavior, the four independent replicates converged to identical modes in their posterior probability distributions.
Effective population sizes:
The resulting marginal posterior distributions for both θ1 and θ2 indicate a large variance in the current effective population sizes among regional human populations (Table 3). As mentioned in the previous section, the current effective sizes of Eurasian populations and one African population (the SE Bantu) are estimated to be very large and all have relatively diffuse marginal posterior distributions. Many of these data sets also have significantly negative values of Tajima's D and Fu and Li's D* statistics (Tables 1 and 2), which indicate rapid population growth. In these cases, modes upward of 100,000 individuals are unlikely to be reliable. In contrast, multilocus data from African and Oceanian populations yield unimodal posterior distributions with modes greater than 10,000 individuals. Table 3 shows that some individual populations have different estimates of the current effective population size in different comparisons. One example is the Dogon population in the Dogon–SE Bantu vs. Dogon–San comparisons. In the highly recombining SE Bantu data set, the estimate of _N_C for the Dogon is much smaller than in the San data set, which has less recombination. One putative explanation for this discrepancy stems from different numbers of segregating sites having to be eliminated due to their failure to pass the four-gamete test in different two-population data sets.
TABLE 3.
Estimates of divergence time (T) and of current (_N_C) and ancestral (_N_A) effective sizes for the 13 comparisons of the 10 sampled human populations
| Population 1 | Population 2 | T (yr) | _N_C1 | _N_A1 | _N_C2 | _N_A2 |
|---|---|---|---|---|---|---|
| Bakola | San | 214,469 | 13,898 | 3,191 | 11,624 | 1,905 |
| San | SE Bantu | 176,527 | 9,644 | 2,917 | 23,153 | 7,004 |
| Bakola | SE Bantu | 174,357 | 7,217 | 7,166 | 23,643 | 4,754 |
| Dogon | SE Bantu | 169,554 | 3,283 | 230 | 29,970 | 4,825 |
| Dogon | San | 145,177 | 9,638 | 4,400 | 9,418 | 3,041 |
| Dogon | Mongolian | 39,496 | 8,794 | 10,128 | 70,489 | 1,494 |
| SE Bantu | Mongolian | 39,449 | 17,672 | 6,403 | 76,731 | 1,251 |
| Mongolian | Dutch | 25,456 | 57,179 | 3,498 | 116,378 | 275 |
| Papuan | Baining | 23,794 | 2,889 | 35 | 1,549 | 4,125 |
| Mongolian | Papuan | 18,596 | 121,053 | 4,405 | 10,800 | 172 |
| Sri Lankan | Dutch | 13,451 | 214,659 | 1,087 | 178,457 | 5,213 |
| Mongolia | Sri Lankan | 11,629 | 55,181 | 4,966 | 437,695 | 2,466 |
| Dutch | Italian | 7,128 | 112,115 | 3,283 | 262,541 | 3,135 |
Estimates of the ancestral effective population size tend to be more uniform across comparisons than estimates of _N_C. Recall that the estimate of _sN_A or (1 − s)_N_A reflects the size of the ancestral population at time T when it split into the two descendant populations. The analysis indicates that only two of the sampled populations have declined in size since their founding, the Dogon of Mali and the Baining of New Britain (Table 3). The estimated intrinsic rate of exponential growth is on the order of 10−4 per year for all other non-African populations, while the rate is on the order of 10−5 for all other African populations (results not shown). This reflects not only the larger current vs. ancestral effective size of non-African populations, but also the older founding times and larger founding effective sizes of the sampled African populations.
The founding effective sizes of many non-African populations are estimated to be quite small, compared with those of African populations. The smallest founding effective size is for the Papua New Guineans and is estimated to be only 35 individuals, with a 95% confidence interval of 30–250 individuals (Table 3). In two comparisons with the Asian populations, the Dutch population shows very small founding sizes, between 172 and 275 individuals, while in comparison with the more recently diverged Italian population the founding size of the Dutch is larger. It is interesting that from the Dogon–Mongolian and the SE Bantu–Mongolian comparisons, the founding non-African population size is estimated to be 1500 individuals, with a 95% confidence interval of 46–2000 individuals. Although divergence times among African populations are more ancient than among non-African populations, the founding effective size of the African populations tends to be larger (Table 3).
Population divergence times:
The marginal posterior distributions for t indicate that divergence times between non-African populations all occur no earlier than the Upper Paleolithic, <40 KYA (Figure 3). The minimum divergence time between non-African populations is from the Dutch–Italian comparison, which yields a marginal posterior distribution with a mode at 7 KYA. The deepest non-African divergence times are the Dutch–Mongolian comparison (25 KYA) and the Baining–Papuan comparison (24 KYA). Alternatively, African populations show substantially deeper divergence times, often >50 KYA (Figure 3). Some within-Africa comparisons yield very old divergence times, although exact estimates are difficult to make because of diffuse posterior distributions. However, posterior distributions for within-Africa divergence times all have well-defined lower bounds. The African and non-African comparisons (Dogon–Mongolian and SE Bantu–Mongolian) indicate that ancestral Eurasian populations split from ancestral African populations as recently as 40 KYA, with a 95% confidence interval of 24–68 KYA.
Rates of gene flow:
The estimated rates of locus-specific unidirectional gene flow for the 13 population comparisons are given in Table 4. There are six cases of highly asymmetrical gene flow, for which the estimated effective number of migrants per generation is high (2_Nm_ ≫ 1) in one direction, but negligible (2_Nm_ ≪ 1) in the other. Between sub-Saharan African populations, asymmetrical rates of gene flow are detected originating from the Dogon into the SE Bantu population for the COIII locus, from the SE Bantu into the Bakola population for the NRY locus, from the San into the SE Bantu for the APXL locus, and in the opposite direction for the X-linked DMD44 locus. The SE Bantu–Dogon comparison is the only one within Africa that shows strong support for gene flow at the mtDNA locus, while all African comparisons show some evidence of gene flow for the NRY locus. Highly asymmetrical rates of gene flow between non-African populations are inferred for the COIII locus originating from the Baining into the Papuan population and for the NRY locus originating from the Papuan into the Mongolian population.
TABLE 4.
Estimates of the locus-specific rates of gene flow per generation (2_Nm_) for the 13 population comparisons
| COIII | NRY | APXL | DMD44 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Population 1 | Population 2 | 2_N_1_m_1 | 2_N_2_m_2 | 2_N_1_m_1 | 2_N_2_m_2 | 2_N_1_m_1 | 2_N_2_m_2 | 2_N_1_m_1 | 2_N_2_m_2 |
| Bakola | San | 0.02 | 1.81 | 5.43 | 2.14 | 0.24 | 0.03 | 3.01 | 0.95 |
| San | SE Bantu | 0.57 | 0.20 | 3.79 | 1.58 | 0.56 | 6.96 | 6.74 | 10.43 |
| Bakola | SE Bantu | 0.02 | 0.09 | 18.24 | 0.15 | 2.82 | 1.12 | 0.12 | 8.85 |
| Dogon | SE Bantu | 0.02 | 92.65 | 6.33 | 1.89 | 19.19 | 19.11 | 8.93 | 22.13 |
| Dogon | San | 0.02 | 1.89 | 1.02 | 3.62 | 6.15 | 6.67 | 0.32 | 1.56 |
| Dogon | Mongolian | 0.23 | 0.25 | 0.17 | 0.19 | 1.83 | 0.08 | 0.05 | 0.15 |
| SE Bantu | Mongolian | 4.09 | 50.83 | 0.58 | 0.74 | 0.38 | 0.65 | 2.38 | 2.74 |
| Mongolian | Dutch | 1.45 | 1.00 | 2.44 | 0.08 | 0.21 | 0.10 | 229.43 | 4.44 |
| Papuan | Baining | 6.25 | 0.23 | 0.03 | 2.16 | 0.56 | 1.41 | 0.51 | 0.04 |
| Mongolian | Papuan | 79.43 | 25.30 | 28.17 | 0.14 | 2.06 | 62.12 | 0.35 | 0.33 |
| Sri Lankan | Dutch | 0.22 | 1.14 | 1.45 | 4.32 | 6.50 | 28.92 | 5.45 | 2.25 |
| Mongolian | Sri Lankan | 123.49 | 11.56 | 72.13 | 159.86 | 0.02 | 1.41 | 29.14 | 821.86 |
| Dutch | Italian | 679.27 | 4690.12 | 493.90 | 860.31 | 2.56 | 296.42 | 662.66 | 446.19 |
High levels of reciprocal gene flow are inferred more often for X-linked loci in comparisons involving both African and non-African populations (Table 4). The only examples of bidirectional gene flow for the haploid loci include the COIII locus in the Mongolian–Papuan comparison and both COIII and NRY in the Dutch–Italian comparison. However, the Dutch–Italian comparison shows high levels of gene flow across all four loci and highly diffuse multilocus marginal posterior distributions for the migration parameters. The Mongolian–Sri Lankan comparison shows high levels of reciprocal gene flow at all loci, except APXL. Notably, the Dutch–Sri Lankan comparison shows relatively low levels of gene flow at all loci, except APXL.
At the level of intercontinental comparisons, there is little gene flow inferred between African and non-African populations, but high levels between Eurasia and Oceania. Only the COIII locus in the SE Bantu–Mongolian shows convincing evidence of gene flow between African and non-African populations. This is not the case for the Dogon–Mongolian comparison, in which all loci show little evidence for historical gene flow. In the Mongolian–Papuan comparison, all loci, except DMD44 show some evidence for either asymmetrical or reciprocal gene flow.
DISCUSSION
The resequencing of four loci from three compartments of the human genome in large samples from each of 10 populations reveals a wide range of nucleotide polymorphism patterns. Sub-Saharan African populations have the highest levels of polymorphism across all four loci, Eurasian populations have lower levels characterized by more low frequency nucleotide variants, while Oceanian populations show the lowest levels of multilocus polymorphism. To understand the demographic processes responsible for these global patterns of polymorphism, a general isolation-with-migration (IM) model was fit to multilocus data sets representing 13 pairwise population comparisons. The parameters of the IM model include current and founding effective population sizes, population divergence times, and rates of gene flow. Parameter estimates portray a complex demographic history for anatomically modern humans over the last 200,000 years.
Diversification and growth of human populations:
The earliest diversification events among the sampled populations are estimated to have occurred among extant sub-Saharan African populations; in some cases these events occurred more than 100 KYA. The oldest diversification dates are estimated to be ∼200 KYA between African hunter-gatherer populations; these times are in close proximity to the estimated time for the emergence of the anatomically modern human phenotype in Africa ∼195 KYA (McDougall et al. 2005). These results suggest that extant African hunter-gatherer populations diversified early in anatomically modern human history. Our estimates of African divergence times generally accord with times previously obtained from studies of classical protein markers, microsatellite, Y chromosome, and mtDNA data (Cavalli-Sforza et al. 1996; Knight et al. 2003; Zhivotovsky et al. 2003). The effective population size of this ancestral African population is estimated to be between 5000 and 11,000 breeding individuals. Three of the four sampled African populations show little evidence for population growth since their divergence.
The founding of non-African populations is estimated to have occurred 40 KYA, with a 95% confidence interval of 24–68 KYA. This range encompasses previous estimates of 40–50 KYA from Y chromosome data (Shen et al. 2000; Thomson et al. 2000), 52–60 KYA from the mtDNA (Watson et al. 1997; Ingman et al. 2000), and 37–57 KYA from autosomal microsatellites (Zhivotovsky et al. 2003). The results of the IM analysis also indicate a severe population bottleneck(s) at the time of the non-African founding event, in which the founding population(s) is estimated to have been only 1500 breeding individuals. Our inferences concerning non-African bottleneck times are consistent with those from studies of single-population demographic history, which estimate non-African bottleneck times at ∼40 KYA (Voight et al. 2005), 27–53 KYA (Reich et al. 2001), and 58–112 KYA (Marth et al. 2004). In the IM model, it is assumed that descendant populations begin exponential growth subsequent to their founding event. This constraint on the inference of bottleneck times in the IM model means that we still cannot definitively address the question of whether human populations began to grow dramatically in the Middle Paleolithic or more recently, during the agricultural revolution of the Neolithic. Moreover, it is not possible to discern the effects of multiple or independent bottlenecks in the history of non-African populations, if they occurred.
Finally, the IM analysis estimates that European and Asian populations were the first non-African populations to diversify, beginning 25 KYA. This divergence time is closely followed by divergence between the two Oceanian populations ∼24 KYA. Within Asia and Europe, divergence times are estimated to be more recent, ranging from 7 to 13 KYA and were accompanied by high levels of population growth. These estimated non-African population diversification times are slightly more recent than published estimates from autosomal protein and microsatellite data (Cavalli-Sforza et al. 1996; Zhivotovsky et al. 2003).
It is interesting to note that at the time of the founding of the ancestral non-African population, three of the four sampled African populations had already split from one another. The conclusion that non-African populations are derived from a structured ancestral African population raises the possibility that only a subset of African populations contributed genetic material to the founding non-African population. This implication is in accord with the conclusions of Satta and Takahata (2004), who argue that the high probability of ancestral haplotypes being found in Africa is most compatible with a model of ancestral African population structure, where some African demes did not participate in the out-of-Africa expansion. One potential avenue for future research would be to calculate divergence times between non-African demes and many thoroughly sampled African demes to find the pair with the minimum divergence time.
Patterns of gene flow:
In the IM model, gene flow between two populations can be assumed to occur with independent rates in each direction. Furthermore, rates of gene flow may be estimated separately for each locus included in the analysis. This permits the estimation of sex-specific migration rates gleaned from the uniparentally-inherited NRY and mtDNA. If high gene flow is defined as more than one effective migrant per generation (i.e., Nm > 1), there are a total of 14 cases of inferred asymmetrical high level gene flow (Table 4). Of these 14 cases, 10 involve the sex-specific haploid loci (8 NRY and 2 COIII) and 4 involve the X-linked loci. Additionally, 9 of the 14 cases are between African populations and 5 involve the non-African comparisons. In contrast, 7 of a total of 19 cases of inferred high levels of reciprocal gene flow involve the haploid loci and 12 involve the X-linked loci.
While all within-Africa comparisons show some evidence of NRY gene flow, most cases of asymmetrical NRY gene flow involve the SE Bantu population. In these comparisons, Y chromosome lineages preferentially emigrate out of the SE Bantu population. The continental expansion of the agricultural Bantu-speaking population approximately 3–4 KYA was likely to be an important event shaping patterns of African genetic diversity (Wood et al. 2005), and may be the cause of these sex-specific gene flow patterns. In the SE Bantu–Bakola comparison, there is support for low levels of gene flow at the COIII locus, but also strong support for Y chromosome gene flow from the SE Bantu into the Bakola, consistent with previous conclusions from Y chromosome studies (Destro-Bisol et al. 2004). There is only one within-Africa comparison in which high levels of gene flow are estimated for the COIII locus: the SE Bantu population preferentially receives female-specific lineages from the Dogon.
High levels of female-specific gene flow appear to be more common between non-African populations than between African populations. Only between the continental European and Asian populations does there appear to be a dearth of female-mediated gene flow (Table 4). The analysis further suggests high levels of gene flow at three of the four sampled loci between continental Asian and Oceanian populations in agreement with the pattern described by Lum et al. (1998), who found low levels of differentiation between Papuans and continental east Asian populations for mtDNA, but high differentiation for autosomal microsatellites. Interestingly, similar to the findings of Wilder and Hammer (2007), gene flow appears to be relatively low between the two Oceanian populations.
One particularly complex pattern of gene flow involves the Sri Lankan population. For three of the four resequencing loci, Sri Lankans are estimated to receive extremely high levels of gene flow from the Mongolian population, while negligible levels are detected in either direction at the APXL locus. Interestingly, when Sri Lankans are analyzed in conjunction with the Dutch sample, there is strong evidence for reciprocal gene flow between the two populations at the APXL locus. Other studies of autosomal markers have noted genetic affinities between Indian and European populations (Bamshad et al. 2001; Watkins et al. 2003). This appears to be a case where the Sri Lankan genome is a mosaic resulting from gene flow from different regional populations.
Predictions of the IM model:
The contrast between patterns of polymorphism seen at loci with different effective population sizes is often informative for inferring historical demographic events, such as population bottlenecks (Fay and Wu 1999). The inferences presented in this article are gleaned from three different compartments of the human genome, each with a different effective population size. However, given the wealth of human autosomal polymorphism data available, it is important to ask: How well do our inferences under the IM model (limited to these four loci) predict patterns of polymorphism seen in larger genomic data sets? To address this question, we simulated under the IM model with parameter values resulting from our analysis.
Because large-scale surveys of resequenced autosomal noncoding polymorphism are currently available for only a single African, Asian, and European population (Hausa, Han Chinese, and Italian; Voight et al. 2005), we substituted the Dogon–Mongolian and Dutch–Mongolian parameter estimates into our simulations for the purpose of comparison. We record the genomic sampling distribution of two summary statistics, _F_ST and Tajima's D, from 10,000 simulated replicates to assess how well they agree with the observed genomic distribution estimated from 50 resequence loci. The ms program was used for coalescent simulations (command lines can be found in supplemental Table S3 at http://www.genetics.org/supplemental/). Figure 4 shows the resulting genomic distributions of the two statistics under our inferred parameterization of the IM model.
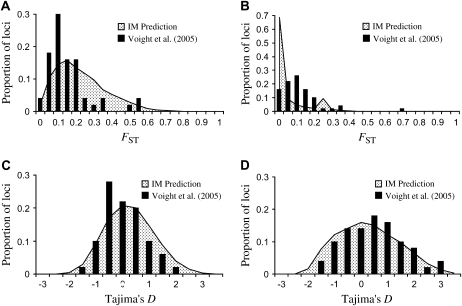
Figure 4.—
Comparison between the distributions of _F_ST values predicted between African and non-African populations (A), under the inferred parameters of the IM model, and those observed at 50 autosomal loci resequenced by Voight et al. (2005). (B) The predicted and observed distributions of _F_ST between European and Asian populations. The predicted and observed distributions of Tajima's D statistic are also given for the African population (C) and the Asian population (D).
To test whether the predicted and observed distributions are sampled from the same underlying probability distribution, a two-sided Kolmogorov–Smirnov test was performed. The observed and predicted distributions for _F_ST between African and non-African populations are significantly different (P < 0.01), with the mean predicted _F_ST = 0.20 and the mean observed _F_ST = 0.14. However, this may represent a difference in the _F_ST values between non-African populations and the Dogon vs. the Hausa, respectively. Likewise, the inferred IM model predicts _F_ST = 0.06 between European and Asian populations, while _F_ST = 0.09 is observed. In this case, the observed and expected distributions are significantly different (P < 0.01). The observed and predicted distributions of African Tajima's D values are not significantly different (P = 0.20), although the data of Voight et al. (2005) have a slightly more negative mean Tajima's D than predicted under the IM model. Finally, differences between the distributions of Asian Tajima's D values are also not statistically significant (P = 0.39), although the mean observed D value is slightly more positive than expected under the IM model.
The inferences under the IM model made here predict a larger degree of genetic divergence between African and non-African populations than is observed. Conversely, the IM model predicts too little genetic differentiation between European and Asian population, compared to the observed distribution. This may be an artifact of obtaining the observed and expected distributions from different populations, or it may reflect the uncertainty in the IM parameter estimates. Unlike, the genetic differentiation statistics, the IM model accurately predicts the observed frequency spectrum statistic. Taken together, these results suggest that the estimates of population size and growth under the IM model may be more reliable than the estimates of divergence time and migration rates.
The problem of unsampled populations:
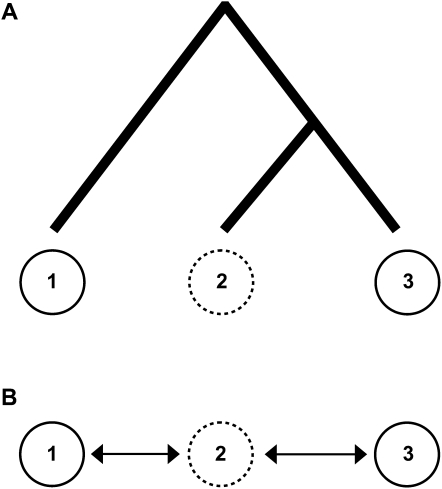
The presence of unsampled populations embedded in a network of populations can be a significant problem for inferring the true pattern of gene flow (Beerli 2004; Slatkin 2005). Unsampled populations can be particularly troublesome in cases of inferred asymmetrical gene flow. One can envision a simple three population model in which populations 1 and 3 are sampled, but intermediary population 2 remains unsampled (Figure 5A). Now, assume that populations 2 and 3 are recently diverged from one another and do not exchange genes, but ongoing gene flow does occur between the more distantly related populations 1 and 2. From this model, there would appear to be asymmetrical gene flow from population 3 into population 1. This “apparent” pattern of gene flow is a byproduct of the fact that unsampled genes in population 2 (that are closely related to genes from population 3) move into population 1, but genes coming from population 1 into population 2 are not sampled and do not migrate into population 3. In this case, the integrity of the biological inference of asymmetrical gene flow between populations 1 and 3 is compromised because, in fact, there is no asymmetrical gene flow occurring at all.
Figure 5.—
A schematic to illustrate the effect of gene flow with unsampled populations. In A, although populations 2 and 3 are more closely related, population 2 only exchanges genes with the more distantly related population 1. If only populations 1 and 3 are sampled (solid circles), this combination of factors may result in a misleading signal of asymmetrical gene flow between populations 1 and 3. However, if gene flow can occur between all populations (sampled or unsampled), as in the linear stepping stone model in B, no such misleading pattern of asymmetrical gene flow is expected.
Concerns over the inference of asymmetrical gene flow are, however, limited to specific models, such as those presented in Figure 5A. The question, as it relates to human populations, becomes, How likely is it that there are closely related, unsampled populations that exchange genes with more distantly related sampled populations? The answer to this question may ultimately depend on how correlated ancestry and geography are in the spatial distribution of extant human populations. The inference problem outlined in the preceding paragraph does not arise in geographically explicit models where all populations (sampled or unsampled) experience nonzero levels of gene flow. For example, consider a linear stepping stone model with intermediary unsampled populations (Figure 5B). If all populations in the network experience gene flow with their neighboring populations, the inference of asymmetrical gene flow from an IM analysis will capture the true pattern of gene flow between the sampled populations. Thus, the misguided inference of asymmetrical gene flow is likely to be restricted to cases where an unsampled portion of a population's range experiences high levels of gene flow.
Conclusions:
While no model can accurately capture all of the processes that affect biological populations, the IM model represents an improvement over traditional models that rely heavily upon the assumptions that populations either do not have shared history apart from gene flow (e.g., Wright's island model), or that populations diverge in isolation. Such generality comes at the expense of the model being parameter rich and thus inference with MCMC techniques can be computationally prohibitive and challenging. Fitting the IM model to this modest four-locus data set confirms and refines previous inferences of a strong non-African population bottleneck(s) and much deeper divergence times between African than non-African populations. However, the IM analysis also suggests a locally dynamic pattern of gene flow and highlights the effect of the expansion of a single population (as exemplified by the Bantu-speaking population) on patterns of within-continent genetic differentiation. Similarly, the IM results suggest a complex relationship between extant sub-Saharan African and non-African populations, in which non-African populations may have descended from only a subset of African populations. Finally, the inference of recurrent population diversification and bottlenecking cautions that explaining human genomic polymorphism may not be achievable through the use of simple, equilibrium models.
Acknowledgments
We thank Zahra Mobasher for excellent technical assistance, A. Di Rienzo for sharing her resequence data, and J. Hey and J. Wakeley for insightful discussion. Publication of this work was made possible by grant GM-53566 from the National Institute of General Medical Sciences (to M.F.H.). Its contents are solely the responsibility of the authors and do not necessarily reflect the official views of the National Institutes of Health.
References
- Bamshad, M., T. Kivisild, W. S. Watkins, M. E. Dixon, C. E. Ricker et al., 2001. Genetic evidence on the origins of Indian caste populations. Genome Res. 11**:** 994–1004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beerli, P., 2004. Effect of unsampled populations on the estimation of population sizes and migration rates between sampled populations. Mol. Ecol. 13**:** 827–836. [DOI] [PubMed] [Google Scholar]
- Beerli, P., and J. Felsenstein, 1999. Maximum-likelihood estimation of migration rates and effective population numbers in two populations using a coalescent approach. Genetics 152**:** 763–773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavalli-Sforza, L. L., P. Menozzi and A. Piazza, 1996. The History and Geography of Human Genes. Princeton University Press, Princeton, NJ.
- Charlesworth, B., D. Charlesworth and N. H. Barton, 2003. The effects of genetic and geographic structure on neutral variation. Annu. Rev. Ecol. Syst. 34**:** 99–125. [Google Scholar]
- Destro-Bisol, G., F. Donati, V. Coia, I. Boschi, F. Verginelli et al., 2004. Variation of female and male lineages in sub-Saharan populations: the importance of sociocultural factors. Mol. Biol. Evol. 21**:** 1673–1682. [DOI] [PubMed] [Google Scholar]
- Fay, J. C., and C. I. Wu, 2000. Hitchhiking under positive Darwinian selection. Genetics 155**:** 1405–1413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fay, J. C., and C. I. Wu, 1999. A human population bottleneck can account for the discordance between patterns of mitochondrial versus nuclear DNA variation. Mol. Biol. Evol. 16**:** 1003–1005. [DOI] [PubMed] [Google Scholar]
- Fu, Y. X., and W. H. Li, 1993. Statistical tests of neutrality of mutations. Genetics 133**:** 693–709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garrigan, D., and M. F. Hammer, 2006. Reconstructing human origins in the genomics era. Nat. Rev. Genet. 7**:** 669–680. [DOI] [PubMed] [Google Scholar]
- Hammer, M. F., F. Blackmer, D. Garrigan, M. W. Nachman and J. A. Wilder, 2003. Human population structure and its effects on sampling Y chromosome sequence variation. Genetics 164**:** 1495–1509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasegawa, M., H. Kishino and T. Yano, 1985. Dating of the human-ape splitting by a molecular clock of mitochondrial DNA. J. Mol. Evol. 22**:** 160–174. [DOI] [PubMed] [Google Scholar]
- Hedrick, P. W., 1999. Perspective: highly variable loci and their interpretation in evolution and conservation. Evolution 53**:** 313–318. [DOI] [PubMed] [Google Scholar]
- Hey, J., 2005. On the number of New World founders: a population genetic portrait of the peopling of the Americas. PLoS Biol. 3**:** e193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hey, J., and R. Nielsen, 2004. Multilocus methods for estimating population sizes, migration rates, and divergence time, with applications to the divergence of Drosophila pseudoobscura and D. persimilis. Genetics 167**:** 747–760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson, R. R., and N. L. Kaplan, 1985. Statistical properties of the number of recombination events in the history of a sample of DNA sequences. Genetics 111**:** 147–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ingman, M., H. Kaessmann, S. Paabo and U. Gyllensten, 2000. Mitochondrial genome variation and the origin of modern humans. Nature 408**:** 708–713. [DOI] [PubMed] [Google Scholar]
- International HapMap Consortium, 2005. A haplotype map of the human genome. Nature 437**:** 1299–1320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorde, L. B., W. S. Watkins, M. J. Bamshad, M. E. Dixon, C. E. Ricker et al., 2000. The distribution of human genetic diversity: a comparison of mitochondrial, autosomal, and Y-chromosome data. Am. J. Hum. Genet. 66**:** 979–988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knight, A., P. A. Underhill, H. M. Mortensen, L. A. Zhivotovsky, A. A. Lin et al., 2003. African Y chromosome and mtDNA divergence provides insight into the history of click languages. Curr. Biol. 13**:** 464–473. [DOI] [PubMed] [Google Scholar]
- Lum, J. K., R. L. Cann, J. J. Martinson and L. B. Jorde, 1998. Mitochondrial and nuclear genetic relationships among Pacific Island and Asian populations. Am. J. Hum. Genet. 63**:** 613–624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marth, G. T., E. Czabarka, J. Murvai and S. T. Sherry, 2004. The allele frequency spectrum in genome-wide human variation data reveals signals of differential demographic history in three large world populations. Genetics 166**:** 351–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maruyama, T., and P. A. Fuerst, 1985. a Population bottlenecks and nonequilibrium models in population genetics. II. Number of alleles in a small population that was formed by a recent bottleneck. Genetics 111**:** 675–689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maruyama, T., and P. A. Fuerst, 1985. b Population bottlenecks and nonequilibrium models in population genetics. III. Genic homozygosity in populations which experience periodic bottlenecks. Genetics 111**:** 691–703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDougall, I., F. H. Brown and J. G. Fleagle, 2005. Stratigraphic placement and age of modern humans from Kibish, Ethiopia. Nature 433**:** 733–736. [DOI] [PubMed] [Google Scholar]
- McVean, G., P. Awadalla and P. Fearnhead, 2002. A coalescent-based method for detecting and estimating recombination from gene sequences. Genetics 160**:** 1231–1241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nei, M., 1987. Molecular Evolutionary Genetics. Columbia University Press, New York.
- Nielsen, R., 2004. Population genetic analysis of ascertained SNP data. Hum. Genomics 1**:** 218–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen, R., and J. Wakeley, 2001. Distinguishing migration from isolation: a Markov chain Monte Carlo approach. Genetics 158**:** 885–896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prugnolle, F., A. Manica and F. Balloux, 2005. Geography predicts neutral genetic diversity of human populations. Curr. Biol. 15**:** R159–R160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ptak, S. E., and M. Przeworski, 2002. Evidence for population growth in humans is confounded by fine-scale population structure. Trends Genet. 18**:** 559–563. [DOI] [PubMed] [Google Scholar]
- Ramachandran, S., O. Deshpande, C. C. Roseman, N. A. Rosenberg, M. W. Feldman et al., 2005. Support from the relationship of genetic and geographic distance in human populations for a serial founder effect originating in Africa. Proc. Natl. Acad. Sci. USA 102**:** 15942–15947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ray, N., M. Currat and L. Excoffier, 2003. Intra-deme molecular diversity in spatially expanding populations. Mol. Biol. Evol. 20**:** 76–86. [DOI] [PubMed] [Google Scholar]
- Reich, D. E., M. Cargill, S. Bolk, J. Ireland, P. C. Sabeti et al., 2001. Linkage disequilibrium in the human genome. Nature 411**:** 199–204. [DOI] [PubMed] [Google Scholar]
- Rogers, E. J., A. C. Shone, S. Alonso, C. A. May and J. A. Armour, 2000. Integrated analysis of sequence evolution and population history using hypervariable compound haplotypes. Hum. Mol. Genet. 9**:** 2675–2681. [DOI] [PubMed] [Google Scholar]
- Romualdi, C., D. Balding, I. S. Nasidze, G. Risch, M. Robichaux et al., 2002. Patterns of human diversity, within and among continents, inferred from biallelic DNA polymorphisms. Genome Res. 12**:** 602–612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satta, Y., and N. Takahata, 2004. The distribution of the ancestral haplotype in finite stepping-stone models with population expansion. Mol. Ecol. 13**:** 877–886. [DOI] [PubMed] [Google Scholar]
- Seielstad, M. T., E. Minch, and L. L. Cavalli-Sforza, 1998. Genetic evidence for a higher female migration rate in humans. Nat. Genet. 20**:** 278–280. [DOI] [PubMed] [Google Scholar]
- Shen, P., F. Wang, P. A. Underhill, C. Franco, W. H. Yang et al., 2000. Population genetic implications from sequence variation in four Y chromosome genes. Proc. Natl. Acad. Sci. USA 97**:** 7354–7359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slatkin, M., 2005. Seeing ghosts: the effect of unsampled populations on migration rates estimated for sampled populations. Mol. Ecol. 14**:** 67–73. [DOI] [PubMed] [Google Scholar]
- Tajima, F., 1983. Evolutionary relationship of DNA sequences in finite populations. Genetics 105**:** 437–460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tajima, F., 1989. Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics 123**:** 585–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teshima, K. M., G. Coop and M. Przeworski, 2006. How reliable are empirical genomic scans for selective sweeps? Genome Res. 16**:** 702–712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomson, R., J. K. Pritchard, P. Shen, P. J. Oefner and M. W. Feldman, 2000. Recent common ancestry of human Y chromosomes: evidence from DNA sequence data. Proc. Natl. Acad. Sci. USA 97**:** 7360–7365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voight, B. F., A. M. Adams, L. A. Frisse, Y. Qian, R. R. Hudson et al., 2005. Interrogating multiple aspects of variation in a full resequencing data set to infer human population size changes. Proc. Natl. Acad. Sci. USA 102**:** 18508–18513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakeley, J., and N. Aliacar, 2001. Gene genealogies in a metapopulation. Genetics 159**:** 893–905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakeley, J., R. Nielsen, S. N. Liu-Cordero and K. Ardlie, 2001. The discovery of single-nucleotide polymorphisms and inferences about human demographic history. Am. J. Hum. Genet. 69**:** 1332–1347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watkins, W. S., A. R. Rogers, C. T. Ostler, S. Wooding, M. J. Bamshad et al., 2003. Genetic variation among world populations: inferences from 100 Alu insertion polymorphisms. Genome Res. 13**:** 1607–1618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watson, E., P. Forster, M. Richards and H. J. Bandelt, 1997. Mitochondrial footprints of human expansions in Africa. Am. J. Hum. Genet. 61**:** 691–704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watterson, G. A., 1975. On the number of segregating sites in genetical models without recombination. Theor. Popul. Biol. 7**:** 256–276. [DOI] [PubMed] [Google Scholar]
- Wilder, J. A., S. B. Kingan, Z. Mobasher, M. M. Pilkington and M. F. Hammer, 2004. Global patterns of human mitochondrial DNA and Y-chromosome structure are not influenced by higher migration rates of females versus males. Nat. Genet. 36**:** 1122–1125. [DOI] [PubMed] [Google Scholar]
- Wilder, J. A., and M. F. Hammer, 2007. Extraordinary population structure among the Baining of New Britain, pp. 199–207 in Genes, Language, and Culture History in the Southwest Pacific, edited by J. S. Friedlaender. Oxford University Press, Oxford.
- Wood, E. T., D. A. Stover, C. Ehret, G. Destro-Bisol, G. Spedini et al., 2005. Contrasting patterns of Y chromosome and mtDNA variation in Africa: evidence for sex-biased demographic processes. Eur. J. Hum. Genet. 13**:** 867–876. [DOI] [PubMed] [Google Scholar]
- Wright, S., 1940. Breeding structure of populations in relation to speciation. Am. Nat. 74**:** 232–248. [Google Scholar]
- Zhivotovsky, L. A., N. A. Rosenberg and M. W. Feldman, 2003. Features of evolution and expansion of modern humans, inferred from genomewide microsatellites. Am. J. Hum. Genet. 72**:** 1171–1186. [DOI] [PMC free article] [PubMed] [Google Scholar]