pi – Store norske leksikon (original) (raw)
Pi i fonten Computer Modern
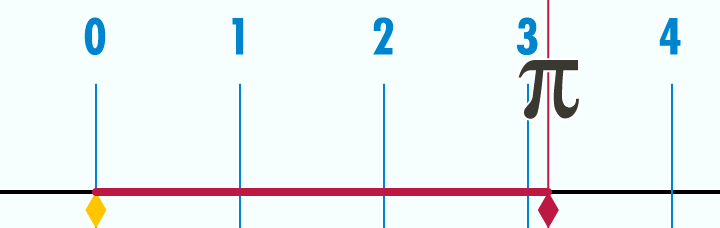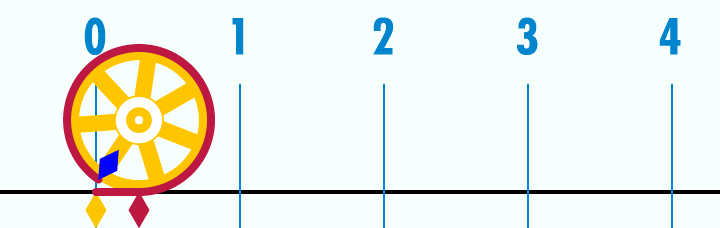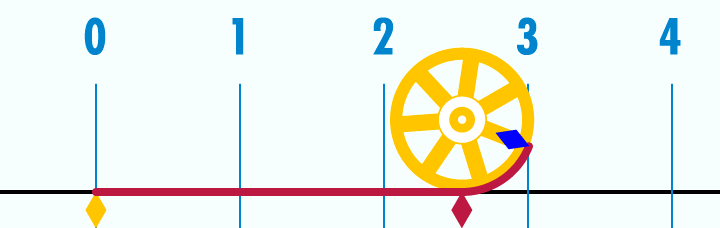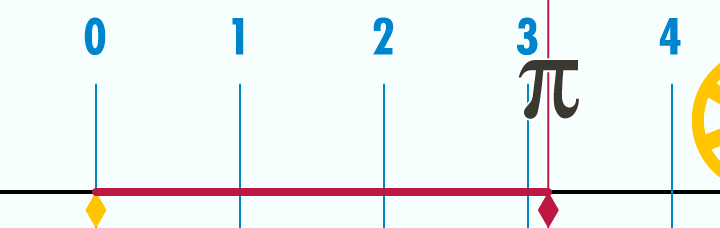
Figuren illustrerer forholdet mellom sirkelens diameter, omkrets og verdien av pi.
Pi er en gresk bokstav som svarer til vår bokstav p. Med greske bokstaver skrives stor pi som Π og liten pi som π.
I matematikken betegner π forholdet mellom omkretsen og diameteren av en sirkel. Omkretsen av en sirkel er altså π ganger så lang som diameteren av den samme sirkelen. Dette kan skrives som \(O = \pi \cdot d\), der O er omkretsen og d er diameteren til sirkelen. Det kan også skrive som \(O = 2 \pi \cdot r\), der r er radiusen.
Videre er arealet av en sirkel gitt som \(A = \pi \cdot r^2\).
Tallet π er omtrent lik 3,141 592 653 589. Det er et irrasjonalt tall med uendelig mange desimaler. Det er dessuten et transcendent tall.
Beregning av π
Ved hjelp av datamaskiner har π blitt beregnet med flere billiarder desimaler. Allerede i oldtiden klarte man å finne tilnærmelsesverdier for π. Arkhimedes beregnet grensene \(3 \frac{10}{71} < \pi < 3 \frac{1}{7}\) ved hjelp av inn- og omskrevne polygoner (mangekanter).
Tallet π forekommer i flere forbindelser i matematikken, og man har funnet mange uendelige uttrykk og rekkeutviklinger for π. Ved å bruke et endelig antall av leddene i en slik rekke finner man en tilnærming til π. Med flere ledd får man en bedre tilnærming, altså flere korrekte desimaler. En av de mest kjente er Leibniz' formel \(\frac{\pi}{4} = 1 – \frac{1}{3} + \frac{1}{5} – \frac{1}{7} + \frac{1}{9} – \frac{1}{11} + \dots\).
Historikk
Betegnelsen π omtales første gang i en engelsk lærebok av William Jones fra 1706, men den kom først i alminnelig bruk gjennom Leonhard Eulers verker.
Johann H. Lambert påviste i 1766 at π er et irrasjonalt tall. Carl Louis Ferdinand von Lindemann beviste i 1882 at π er et transcendent tall, det vil si at det ikke er rot i noen algebraisk ligning med rasjonale koeffisienter. Av dette følger at problemet med sirkelens kvadratur er uløselig. Det betyr at det er umulig å konstruere (med passer og linjal) et kvadrat med samme areal som en gitt sirkel.