Магнитный диполь | это... Что такое Магнитный диполь? (original) (raw)

Классическая электродинамика

Магнитное поле соленоида
Электричество · Магнетизм Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Электродинамика Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-ток · 4-потенциал Известные учёные Генри Кавендиш Майкл Фарадей Андре-Мари Ампер Густав Роберт Кирхгоф Джеймс Клерк (Кларк) Максвелл Генри Рудольф Герц Альберт Абрахам Майкельсон Роберт Эндрюс Милликен

Магнитное поле Земли примерно совпадает с полем диполя. Однако «N» и «S» (северный и южный) полюса отмечены «географически», то есть противоположно принятому обозначению для полюсов магнитного диполя.

Диполь — идеализированная система, служащая для приближенного описания распространения поля. Дипольное приближение основано на разложении потенциалов поля в ряд по степеням радиус-вектора и отбрасывании всех членов выше первого порядка. Полученные функции будут эффективно описывать поле в случае если

Размеры излучающей поле системы малы по сравнению с рассматриваемыми расстояниями, так что отношение характерного размера системы к длине радиус-вектора является малой величиной и имеет смысл рассмотрение лишь первых членов разложения потенциалов в ряд.
Член первого порядка в разложении не равен 0, в противном случае нужно использовать приближение более высокой мультипольности.
В уравнениях рассматриваются градиенты потенциалов не выше первого порядка.

Типичный пример диполя — два бесконечно близких заряда, равных по величине и противоположных по знаку. Поле такой системы полностью описывается дипольным приближением.

Содержание

1 Дипольный момент системы
- 1.1 Электрический диполь
- 1.2 Магнитный диполь
2 Поле колеблющегося диполя
- 2.1 Поле на близких расстояниях
- 2.2 Дипольное излучение (излучение в волновой зоне)
3 Литература
4 См. также

Дипольный момент системы

Эквипотенциальные поверхности электрического диполя

Электрический диполь

Силовые линии электрического диполя

Электрический диполь — идеализированная электронейтральная система, состоящая из точечных и равных по абсолютной величине положительного и отрицательного электрических зарядов.

Другими словами, электрический диполь представляет из себя совокупность двух равных по абсолютной величине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга

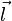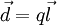Произведение вектора $\vec l$ , проведённого от отрицательного заряда к положительному, на абсолютную величину зарядов $q\,$ , называется дипольным моментом: $\vec d=q\vec l$ .

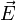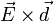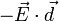Во внешнем электрическом поле $\vec E$ на диполь действует момент сил ${\vec E}\times{\vec d}$ , который стремится повернуть его так, чтобы дипольный момент развернулся вдоль направления поля. Потенциальная энергия диполя в электрическом поле равна $-{\vec E}\cdot{\vec d}$ .

Вдали от диполя напряжённость его электрического поля убывает с расстоянием R как 1 / _R_3, то есть быстрее, чем у точечного заряда.

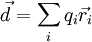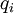Любая электронейтральная система в некотором приближении может рассматриваться как электрический диполь с моментом $\vec d = \sum_i q_i {\vec r}_i$ , где $q_i\,$ — заряд _i_-го элемента, 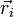${\vec r}_i$ — его радиус-вектор. При этом дипольное приближение будет корректным, если расстояние, на котором изучается электрическое поле системы, велико по сравнению с её характерными размерами.

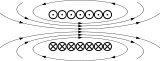
Магнитный диполь

Магнитный диполь — аналог электрического, который можно представить себе как систему двух «магнитных зарядов» (эта аналогия условна, так как магнитных зарядов, с точки зрения современной электродинамики, не существует). В качестве модели магнитного диполя можно рассматривать небольшую (по сравнению с расстояниями, на которых изучается генерируемое диполем магнитное поле) плоскую замкнутую проводящую рамку площади 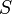$S\,$ , по которой течёт ток 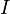$I\,$ . 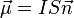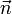При этом магнитным моментом диполя (в системе СГСМ) называют величину ${\vec \mu} = I S {\vec n}$ , где ${\vec n}$ — единичный вектор, направленный перпендикулярно плоскости рамки в том направлении, с которого ток в рамке течёт против часовой стрелки.

Поле колеблющегося диполя

В этом разделе рассматривается поле, создаваемое точечным электрическим диполем 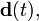$\mathbf{d}(t),$ находящимся в заданной точке пространства.

Поле на близких расстояниях

Эволюция поля колеблющегося электрического диполя в реальном времени. Диполь находится в точке (60,60) и колеблется по вертикали с частотой 1 рад/с (~0.16 Гц)

Поле точечного диполя, колеблющегося в вакууме, имеет вид

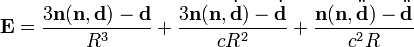
$\mathbf{E} = \frac{3 \mathbf{n} (\mathbf{n}, \mathbf{d})-\mathbf{d}}{R^3} + \frac{3 \mathbf{n} (\mathbf{n}, \dot \mathbf{d}) - \dot \mathbf{d}}{c R^2} + \frac{ \mathbf{n} (\mathbf{n}, \ddot \mathbf{d}) - \ddot \mathbf{d}}{c^2 R}$

$\mathbf{B} = \left[\frac{\dot \mathbf{d}}{c R^2} + \frac{\ddot \mathbf{d}}{R c^2} , \mathbf{n} \right] = \left[\mathbf{n} , \mathbf{E} + \frac{\mathbf{d}}{R^3}\right]$ ,

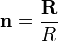где $\mathbf{n} = \frac{\mathbf{R}}{R}$ — единичный вектор в рассматриваемом направлении, c — скорость света.

Этим выражениям можно придать несколько другую форму, если ввести вектор Герца

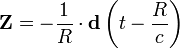
$\mathbf{Z} = - \frac{1}{R} \cdot \mathbf{d}\left(t-\frac{R}{c}\right)$

Напомним, что диполь покоится в начале координат, так что 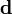$\mathbf{d}$ является функцией одной переменной. Тогда

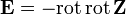
$\mathbf{E} = - \operatorname{rot}\,\operatorname{rot}\,\mathbf{Z}$

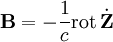
$\mathbf{B} = - \frac{1}{c}\operatorname{rot}\,\dot\mathbf{Z}$

При этом потенциалы поля можно выбрать в виде

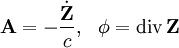
$\mathbf{A} = - \frac{\dot \mathbf{Z}}{c}, ~~ \phi = \operatorname{div}\,\mathbf{Z}$

Указанные формулы можно применять всегда, когда применимо дипольное приближение.

Дипольное излучение (излучение в волновой зоне)

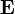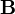Приведённые формулы существенно упрощаются, если размеры системы много меньше длины излучаемой волны, то есть скорости зарядов много меньше c, а поле рассматривается на расстояниях много больших, чем длина волны. Такую область поля называют волновой зоной. Распространяющуюся волну можно в этой области считать практически плоской. Из всех членов в выражениях для $\mathbf{E}$ и $\mathbf{B}$ существенными оказываются только члены, содержащие вторые производные от 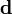$\mathbf{d}$ , так как

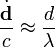
$\frac{\dot \mathbf{d}}{c} \approx \frac{d}{\lambda}$

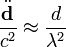
$\frac{\ddot \mathbf{d}}{c^2} \approx \frac{d}{\lambda^2}$

Выражения для полей принимают вид

$\mathbf{B} = \frac{1}{c^2 R}[\ddot \mathbf{d},\mathbf{n}], ~~ \mathbf{B} = [\mathbf{n} , \mathbf{E}]$

![\mathbf{E} = \frac{1}{c^2 R}\left[ [\ddot \mathbf{d},\mathbf{n}] , \mathbf{n} \right], ~~ \mathbf{E} = [\mathbf{B} , \mathbf{n}]](https://dic.academic.ru/pictures/wiki/files/101/ee8c127945423b770e8bdd993be8375a.png)

В плоской волне интенсивность излучения в телесный угол d o равна

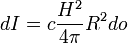$dI = c \frac{H^2}{4\pi}R^2 do$ ,

поэтому для дипольного излучения

$dI = \frac{1}{4 \pi c^3}[\ddot \mathbf{d}, \mathbf{n}]^2 do = \frac{\ddot d^2}{4\pi c^3}\sin^2{\theta} do$

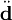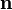где θ — угол между векторами $\ddot\mathbf{d}$ и $\mathbf{n}$ . Найдём полную излучаемую энергию. Учитывая, что 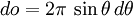$do = 2\pi\, \sin{\theta}\, d\theta$ , проинтегрируем выражение по _d_θ от 0 до π. Полное излучение равно

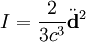
$I = \frac{2}{3 c^3} {\ddot\mathbf{d}}^2$

Укажем спектральный состав излучения. Он получается заменой вектора 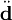$\ddot \mathbf{d}$ на его Фурье-компоненту и одновременным умножением выражения на 2. Таким образом:

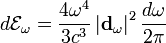
$d \mathcal{E}_\omega = \frac{4 \omega^4}{3 c^3} \left| \mathbf{d}_\omega \right|^2 \frac{d\omega}{2\pi}$

Литература

Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7

См. также

Структурная химия
Химическая связь:	Ароматичность \| Ковалентная связь	Ионная связь	Металлическая связь	Водородная связь	Донорно-акцепторная связь	Таутомерия
Отображение структуры:	Функциональная группа \| Структурная формула	Химическая формула	Лиганд
Электронные свойства:	Электроотрицательность \| Сродство к электрону	Энергия ионизации	Диполь	Правило октета
Стереохимия:	Асимметрический атом \| Изомерия	Конфигурация	Хиральность	Конформация

Wikimedia Foundation.2010.