Проблема слабого CP-нарушения | это... Что такое Проблема слабого CP-нарушения? (original) (raw)

В физике элементарных частиц нарушение _CP_-инвариантности — это нарушение постулируемой _CP_-симметрии законов физики. Оно играет важную роль в теориях космологии, которые пытаются объяснить превосходство материи над антиматерией в нашей Вселенной. Открытие нарушения _CP_-симметрии в 1964 г. в процессах распада нейтральных каонов привело к Нобелевской премии по физике в 1980 г. для его первооткрывателей Джеймса Кронина и Вэла Фитча. В 1967 г., Андрей Сахаров показал, что _CP_-нарушение являлось одним из необходимых условий для практически полного уничтожения антивещества на раннем этапе развития Вселенной. В 1973 г., пытаясь найти объяснение _CP_-нарушению в распадах нейтральных каонов и отталкиваясь от идеи Николы Кабиббо о смешивании двух поколений кварков, Макото Кобаяши и Тошихидэ Маскава предсказали существование третьего. Действительно, _b_-кварк был открыт в 1977 г., _t_-кварк - в 1995. Предсказанные теорией Кобаяши и Маскавы различия свойств B и анти-B мезонов, включая прямое _CP_-нарушение, были открыты на экспериментах Нобелевской премии по физике 2008 г.

Содержание

Что такое CP?

CP — это произведение двух симметрий: C — зарядовое сопряжение, которое превращает частицу в ее античастицу, и P — чётность, которая создает зеркальное изображение физической системы. Сильное взаимодействие и электромагнитное взаимодействие являются инвариантными по отношению к комбинированной операции CP преобразования, но эта симметрия немного нарушается в процессе некоторых типов слабого распада. Исторически CP-симметрия была предложена для восстановления порядка после открытия нарушения чётности в 1950-е.

Идея симметрии чётности в том, что уравнения физики инвариантны относительно зеркальной инверсии. Это ведет к предсказанию того, что зеркальное изображение реакции (например, химической реакции или радиоактивного распада) происходит также как и сама реакция. Симметрия чётности соблюдается для всех реакций, связанных с электромагнетизмом и сильными взаимодействиями. До 1956 г. закон сохранения чётности считался одним из фундаментальных геометрических законов сохранения (как и закон сохранения энергии и закон сохранения импульса). Однако в 1956 г. тщательный критический анализ накопленных экспериментальных данных физиками Чжэндао Ли и Чжэньнин Янг выявил, что сохранение четности не проверялось в процессах слабого взаимодействия. Они предложили несколько возможных экспериментов. Первый эксперимент был основан на бета-распаде ядер кобальта-60 и был проведён в 1956 г. группой под руководством Ву Цзяньсюн, и показали, что в процессах слабого взаимодействия P-симметрия нарушается или, как можно показать, некоторые реакции происходят не так же часто, как их зеркальные двойники.

В общем и целом, симметрия квантовомеханической системы может быть восстановлена, если будет найдена другая симметрия S так, что общая симметрия PS останентся ненарушенной. Это хитрое место в структуре Гильбертова пространства было осознано вскоре после открытия нарушения чётности, и зарядовое сопряжение было предложено в качестве искомой симметрии для восстановления порядка.

Попросту говоря, зарядовое сопряжение — это простая симметрия между частицами и античастицами, так что CP-симметрия была предложена в 1957 г. Львом Ландау как истинная симметрия между материей и антиматерией. Другими словами, процесс, в котором все частицы меняются со своими античастицами, считается эквивалентным зеркальному отображению данного процесса.

Нарушение CP-симметрии

Диаграмма каонной осцилляции

Эти две диаграммы — диаграммы Фейнмана, представляющие основные вклады в амплитуду каонной (K-Kbar) осцилляции

В 1964 г. Джеймс Кронин и Вэл Фитч показали (впервые об этом было объявлено на 12-й Дубне), что CP-симметрия тоже может быть нарушена, за это открытие им досталась Нобелевская премия по физике 1980 г. Их открытие показало, что слабые взаимодействия нарушают не только симметрию зарядового сопряжения C между частицами и античастицами и симметрию чётности P, но также и их комбинацию. Открытие потрясло физику элементарных частиц и подняло вопросы, до сих пор требующие ответа в самом сердце физики элементарных частиц и космологии. Отсутствие точной CP-симметрии, но также и факт, что симметрия почти соблюдается, создали великую загадку.

В 1964 г. Кристенсоном, Крониным, Фитчем и Тёрлеем было открыто нарушение CP-симметрии в экспериментах по распаду каонов; в физических явлениях сохраняется только более слабый вариант симметрии — CPT-инвариантность. Кроме C и P, существует третья операция — обращение времени (T), которая соответствует обратимости движения. Инвариантность относительно обращения времени означает, что если движение разрешено законами физики, то обратное движение также разрешено. Комбинация CPT составляет точную симметрию всех типов фундаментальных взаимодействий. Из-за CPT-симметрии нарушение CP-симметрии эквивалентно нарушению T-симметрии. Нарушение CP-симметрии предполагает несохранение T, исходя из предположения, что CPT-теорема верна. В этой теореме, которая считается одним из основных принципов квантовой теории поля, зарядовое сопряжение, чётность и обращение времени применяются вместе.

Тип нарушения CP-симметрии, открытый в 1964 г., был связан с тем фактом, что нейтральные каоны могут превращаться в свои античастицы (в которых кварки заменяются антикварками) и наоборот, но подобное превращение не происходит с одинаковой вероятностью в обоих направлениях; это было названо косвенным нарушением CP-симметрии.

Несмотря на масштабные поиски, других признаков нарушения CP-симметрии не было известно до 1990-х, когда результаты эксперимента NA31 в ЦЕРНе доказали нарушение CP-симметрии в процессах распада все тех же нейтральных каонов, так называемое прямое нарушение CP-симметрии. Открытие было спорным, и окончательное доказательство пришло лишь в 1999 г. после экспериментов KTeV в Фермилабе и экспериментов NA48 в ЦЕРНе.

В 2001 г. в новом поколении экспериментов, включая эксперимент SLAC) и эксперимент Белль при Организации по исследованиям на ускорителях высоких энергий — Япония (КЕК), наблюдалось нарушение CP-симметрии, используя B-мезоны [1]. До этих экспериментов была вероятность того, что нарушение CP-симметрии ограничивается физикой каонов. Эти эксперименты развеяли все сомнения в том, что взаимодействия Стандартной модели нарушают CP. В 2007 г., подобные эксперименты показали существование и прямого нарушения CP-симметрии для B-мезонов (см. ссылки).

Нарушение CP-симметрии включается в Стандартную модель посредством включения комплексной фазы в CKM-матрицу, описывающей смешивание кварков. В такой схеме необходимым условием для появления комплексной фазы и нарушения CP-симметрии является существование по меньшей мере трёх поколений кварков.

Нет никаких экспериментальных подтверждений нарушения CP-симметрии в квантовой хромодинамике; см. ниже.

Сильная CP-проблема

В физике элементарных частиц сильная CP-проблема — это загадочный вопрос, почему в квантовой хромодинамике (КХД) не нарушается CP-симметрия.

КХД не нарушает CP-симметрию также просто, как и теория электрослабого взаимодействия; в отличие от электрослабой теории, в которой калибровочные поля связываются в киральные токи, созданные фермионными полями, глюоны связываются в векторные токи. Эксперименты не показывают никакого нарушения CP-симметрии в области КХД. Например, общее нарушение CP-симметрии в области КХД создало бы электрический дипольный момент у нейтрона, который был бы порядка 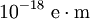10^{-18}\ \rm{e\cdot{}m} (заряд электрона, умноженный на метр), в то время как экспериментальная верхняя граница приблизительно в триллион раз меньше.

Это проблема, потому что в конце концов есть естественные члены в лагранжиане КХД, которые могут нарушать CP-симметрию.

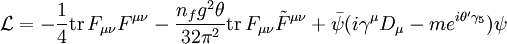
{\mathcal L} = -\frac{1}{4} {\mathrm {tr}\,} F_{\mu\nu}F^{\mu\nu}-\frac{n_f g^2\theta}{32\pi^2} {\mathrm {tr}\,}F_{\mu\nu}\tilde F^{\mu\nu}+\bar \psi(i\gamma^\mu D_\mu - m e^{i\theta'\gamma_5})\psi

При ненулевом выборе КХД θ-угла и хиральной фазы кварковой массы θ' можно ожидать, что CP-симметрия будет нарушена. Обычно считается, что хиральная фаза кварковой массы может стать вкладом в общий эффективный 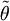\tilde\theta-угол, но остаётся необъяснённым, почему Природа выбрала невероятно малое значение этого угла вместо произвольного значения между 0 и 2π; специальный выбор θ-угла, очень близкого к нулю (в этом случае), является примером точной настройки в физике.

Нарушение CP-симметрии и дисбаланс между материей и антиматерией

Один из нерешенных теоретических вопросов в физике — почему вселенная состоит в основном из материи, а не из равных частей материи и антиматерии. Можно показать, что для создания дисбаланса между материей и антиматерией из начального баланса, должны быть удовлетворены условия Сахарова, одним из которых является нарушение CP-симметрии в экстремальных условиях первых секунд после Большого взрыва. Объяснения, не использующие нарушение CP-симметрии, менее удачны, поскольку они покоятся на предположении, что дисбаланс материя-антиматерия существовал изначально или на других экзотических предположениях.

После Большого взрыва должны были появиться одинаковые количества материи и антиматерии, если CP-симметрия сохранялась; в таком случае, произошла бы тотальная аннигиляция обоих. То есть, нуклоны аннигилировали бы с антинуклонами, электроны с позитронами, и так далее для всех элементарных частиц. Это бы привело к морю фотонов во вселенной без материи. Поскольку очевидно, что наша вселенная не море фотонов без материи, после Большого взрыва физические законы действовали по-разному для материи и антиматерии, то есть нарушалась CP-симметрия.

Стандартная модель предполагает только два пути нарушения CP-симметрии. Один из них, о котором шла речь выше, содержится в лагранжиане КХД и экспериментально не доказан; можно ожидать, что он приведёт либо к отсутствию нарушения симметрии, либо к намного более сильному нарушению этой симметрии. Второй из них, использующий слабое взаимодействие, был экспериментально проверен, но может служить объяснением только для малой части нарушений CP-симметрии. Предсказано, что он достаточен для чистой массы нормальной материи, эквивалентной всего лишь одной галактике в известной вселенной.

Поскольку Стандартная модель не достаточно аккуратно объясняет эти расхождения, становится ясно, что текущая Стандартная модель имеет серьезные дыры (помимо очевидной с гравитацией). Более того, эксперименты по заполнению этих связанных с CP-симметрией дыр не требуют практически невозможных энергий, как того требуют исследования по квантовой гравитации (см. Планковская масса).

Ссылки

Wikimedia Foundation.2010.