Гармонический осциллятор | это... Что такое Гармонический осциллятор? (original) (raw)

У этого термина существуют и другие значения, см. Осциллятор.

Гармони́ческий осцилля́тор (в классической механике) — система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x (согласно закону Гука):

$F = -k x \,$

где k — коэффициент жёсткости системы.

Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.

Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.

Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами отклонения), груз на пружине, торсионный маятник и акустические системы. Среди других аналогов гармонического осциллятора стоит выделить электрический гармонический осциллятор (см. LC-цепь).

Содержание

1 Свободные колебания
- 1.1 Консервативный гармонический осциллятор
  * 1.1.1 Простое гармоническое движение
  * 1.1.1.1 Динамика простого гармонического движения
  * 1.1.1.2 Энергия простого гармонического движения
  * 1.1.1.3 Примеры
  * 1.1.1.3.1 Груз на пружине
  * 1.1.1.3.2 Универсальное движение по окружности
  * 1.1.1.3.3 Груз как простой маятник
- 1.2 Затухающий гармонический осциллятор
2 Вынужденные колебания
3 Литература
4 См. также
5 Примечания

Свободные колебания

Консервативный гармонический осциллятор

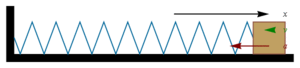
В качестве модели консервативного гармонического осциллятора возьмём груз массы m, закреплённый на пружине жёсткостью k.

Пусть x — смещение груза относительно положения равновесия. Тогда, согласно закону Гука, на него будет действовать возвращающая сила:

$F = -k x. \,$

Используя второй закон Ньютона, запишем

$a = -\frac{k}{m}x. \,$

Обозначая ${\omega_0}^2 = k/m$ и заменяя ускорение a на вторую производную от координаты по времени $\ddot x,$ напишем:

$\ddot x + \omega_0^2 x = 0.$

Это дифференциальное уравнение описывает поведение консервативного гармонического осциллятора. Коэффициент $\omega_0$ называют циклической частотой осциллятора. (Здесь имеется в виду круговая частота, измеряющаяся в радианах в секунду. Чтобы перевести её в частоту, выражающуюся в Герцах, надо разделить круговую частоту на $2 \pi$ )

Будем искать решение этого уравнения в виде:

$x(t) = A \sin\left(\omega t + \varphi\right).$

Здесь A — амплитуда, ω — частота колебаний (пока не обязательно равная собственной частоте), φ — начальная фаза.

Подставляем в дифференциальное уравнение.

$\ddot x (t) = -A \omega^2 \sin(\omega t + \varphi),$

$-A \omega^2 \sin(\omega t + \varphi) + \omega_0^2 A \sin(\omega t + \varphi) = 0.$

Амплитуда сокращается. Значит, она может иметь любое значение (в том числе и нулевое — это означает, что груз покоится в положении равновесия). На синус также можно сократить, так как равенство должно выполняться в любой момент времени t. Таким образом, остаётся условие на частоту колебаний:

$-\omega^2 + \omega_0^2 = 0,$

$\omega = \pm \omega_0.$

Отрицательную частоту можно отбросить, так как произвол в выборе этого знака покрывается произволом выбора начальной фазы.

движение по кругу и движение гармоническое

Общее решение уравнения записывается в виде:

$x(t) = A \sin\left(\omega_0 t + \varphi\right),$

где амплитуда A и начальная фаза φ — произвольные постоянные. Эта запись исчерпывает все решения дифференциального уравнения, так как позволяет удовлетворить любым начальным условиям (начальному положению груза и его начальной скорости).

Итого, консервативный гармонический осциллятор может совершать чисто гармонические колебания с частотой, равной его собственной частоте, с амплитудой любой величины и с произвольной начальной фазой.

Кинетическая энергия записывается в виде

$T = \frac{1}{2} m \left(\frac{dx}{dt}\right)^2 = \frac{1}{2} k A^2 \cos^2(\omega_0 t + \varphi),$

и потенциальная энергия есть

$U = \frac{1}{2} k x^2 = \frac{1}{2} k A^2 \sin^2(\omega_0 t + \varphi),$

тогда полная энергия имеет постоянное значение

$E = \frac{1}{2} k A^2.$

Простое гармоническое движение

Простое гармоническое движение — это движение простого гармонического осциллятора, периодическое движение, которое не является ни вынужденным, ни затухающим. Тело в простом гармоническом движении подвергается воздействию единственной переменной силы, которая по модулю прямо пропорциональна смещению x от положения равновесия и направлена в обратную сторону.

Это движение является периодическим: тело колеблется около положения равновесия по синусоидальному закону. Каждое последующее колебание такое же, как и предыдущее, и период, частота и амплитуда колебаний остаются постоянными. Если принять, что положение равновесия находится в точке с координатой, равной нулю, то смещение x тела от положения равновесия в любой момент времени даётся формулой:

$x(t) = A\cos\left(2\pi\!f t+\varphi\right),$

где A — амплитуда колебаний, f — частота, φ — начальная фаза.

Частота движения определяется характерными свойствами системы (например, массой движущегося тела), в то время как амплитуда и начальная фаза определяются начальными условиями — перемещением и скоростью тела в момент начала колебаний. Кинетическая и потенциальная энергии системы также зависят от этих свойств и условий.

Простое гармоническое движение. На этой анимированной картинке по вертикальной оси отложена координата частицы (x в формуле), а по горизонтальной оси отложено время (t).

Простое гармоническое движение может быть математическими моделями различных видов движения, таких как колебание пружины. Другими случаями, которые могут приближённо рассматриваться как простое гармоническое движение, являются движение маятника и вибрации молекул.

Простое гармоническое движение является основой некоторых способов анализа более сложных видов движения. Одним из таких способов является способ, основанный на преобразовании Фурье, суть которого сводится к разложению более сложного вида движения в ряд простых гармонических движений.

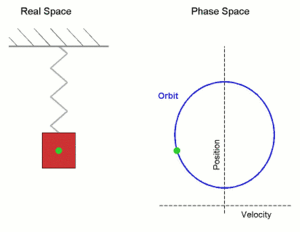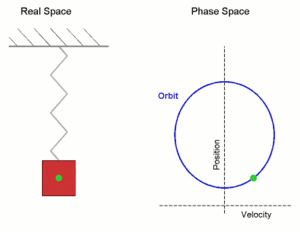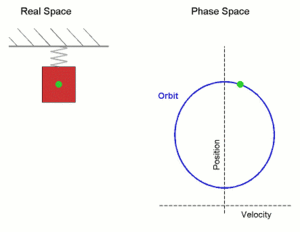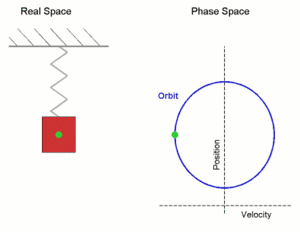
Простое гармоническое движение, показанное одновременно в реальном пространстве и в фазовом пространстве. Здесь ось скорости и ось положения показаны иначе по сравнению с обычным изображением осей координат — это сделано для того, чтобы оба рисунка соответствовали друг другу. Real Space — реальное пространство; Phase Space — фазовое пространство; velocity — скорость; position — положение (позиция).

Типичным примером системы, в которой происходит простое гармоническое движение, является идеализированная система груз-пружина, в которой груз присоединён к пружине. Если пружина не сжата и не растянута, то на груз не действует никаких переменных сил, и груз находится в состоянии механического равновесия. Однако, если груз вывести из положения равновесия, пружина деформируется, и с её стороны на груз будет действовать сила, которая будет стремиться вернуть груз в положение равновесия. В случае системы груз-пружина такой силой является сила упругости пружины, которая подчиняется закону Гука:

F = -kx,

где

F — возвращающая сила,

x — перемещение груза (деформация пружины),

k — коэффициент жёсткости пружины.

Любая система, в которой происходит простое гармоническое движение, обладает двумя ключевыми свойствами:

Когда система выведена из состояния равновесия, должна существовать возвращающая сила, стремящаяся вернуть систему в равновесие.
Возвращающая сила должна в точности или приближённо быть пропорциональна перемещению.

Система груз-пружина удовлетворяет обоим этим условиям.

Однажды смещённый груз подвергается действию возвращающей силы, ускоряющей его, и стремящейся вернуть в начальную точку, то есть, в положение равновесия. По мере того, как груз приближается к положению равновесия, возвращающая сила уменьшается и стремится к нулю. Однако в положении x = 0 груз обладает некоторым количеством движения (импульсом), приобретённым благодаря действию возвращающей силы. Поэтому груз проскакивает положение равновесия, начиная снова деформировать пружину (но уже в противоположном направлении). Возвращающая сила будет стремиться замедлить его, пока скорость не станет равной нулю; и сила вновь будет стремиться вернуть груз в положение равновесия.

Пока в системе нет потерь энергии, груз будет колебаться как описано выше; такое движение называется периодическим.

Дальнейший анализ покажет, что в случае системы груз-пружина движение является простым гармоническим.

Динамика простого гармонического движения

Для колебания в одномерном пространстве, учитывая Второй закон Ньютона (F = m d²_x_/d_t_²) и закон Гука (F = −kx, как описано выше), имеем линейное дифференциальное уравнение второго порядка:

$m\frac{\mathrm{d}^2 x}{\mathrm{d}t^2} = -kx,$

где

m — масса тела,

x — его перемещение относительно положения равновесия,

k — постоянная (коэффициент жёсткости пружины).

Решение этого дифференциального уравнения является синусоидальным; одно из решений таково:

$x(t) = A\cos(\omega t + \varphi),$

где A, ω и φ — постоянные величины, и положение равновесия принимается за начальное.[1] Каждая из этих постоянных представляет собой важное физическое свойство движения: A — это амплитуда, ω = 2π_f_ — круговая частота, и φ — начальная фаза.[2]

Положение, скорость и ускорение гармонического осцилятора

Используя приёмы дифференциального исчисления, скорость и ускорение как функция времени могут быть найдены по формулам:

$v(t) = \frac{\mathrm{d} x}{\mathrm{d} t} = - A\omega \sin(\omega t+\varphi),$

$a(t) = \frac{\mathrm{d}^2 x}{\mathrm{d}t^2} = - A \omega^2 \cos( \omega t+\varphi).$

Положение, скорость и ускорение простого гармонического движения на фазовой плоскости

Ускорение может быть также выражено как функция перемещения:

$a(x) = -\omega^2 x.\!$

Поскольку ma = −m_ω²_x = −kx, то

$\omega^2 = \frac{k}{m}.$

Учитывая, что ω = 2π_f_, получим

$f = \frac{1}{2\pi}\sqrt{\frac{k}{m}},$

и поскольку T = 1/f, где T — период колебаний, то

$T = 2\pi\sqrt{\frac{m}{k}}.$

Эти формулы показывают, что период и частота не зависят от амплитуды и начальной фазы движения.

Энергия простого гармонического движения

Кинетическая энергия K системы в зависимости от времени t такова:

$K(t) = \frac{1}{2} mv(t)^2 = \frac{1}{2}m\omega^2A^2\sin^2(\omega t + \varphi) = \frac{1}{2}kA^2 \sin^2(\omega t + \varphi),$

и потенциальная энергия есть

$U(t) = \frac{1}{2} k x(t)^2 = \frac{1}{2} k A^2 \cos^2(\omega t + \varphi).$

Полная механическая энергия системы, однако, имеет постоянное значение

$E = K + U = \frac{1}{2} k A^2.$

Примеры

Система груз-пружина без затухания, в которой происходит простое гармоническое движение.

Простое гармоническое движение представлено в различных простых физических системах, и ниже приведены некоторые примеры.

Груз на пружине

Масса m, прикреплённая к пружине с постоянной жёсткостью k, является примером простого гармонического движения в пространстве. Формула

$T= 2 \pi \sqrt{\frac{m}{k}}$

показывает, что период колебаний не зависит от амплитуды и ускорения свободного падения.

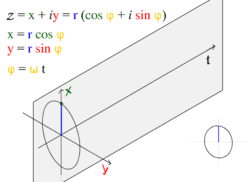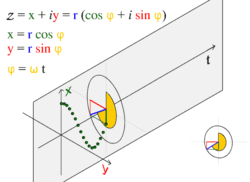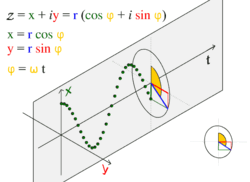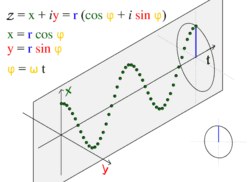
Универсальное движение по окружности

Простое гармоническое движение в некоторых случаях можно рассматривать как одномерная проекция универсального движения по окружности. Если объект движется с постоянной угловой скоростью ω по окружности радиуса r, центром которой является начало координат плоскости x − y, то такое движение вдоль каждой из координатных осей является простым гармоническим с амплитудой r и круговой частотой ω.

Груз как простой маятник

Движение маятника, не имеющего затуханий, можно приближённо рассматривать как простое гармоническое движение, если амплитуда колебаний очень мала в сравнении с длиной стержня.

В приближении малых углов движение простого маятника является близким к простому гармоническому. Период колебаний такого маятника, прикреплённого к стержню длиной ℓ с ускорением свободного падения g даётся формулой

$T = 2 \pi \sqrt{\frac{\ell}{g}}.$

Это показывает, что период колебаний не зависит от амплитуды и массы маятника, но зависит от ускорения свободного падения g, поэтому при той же самой длине маятника, на Луне он будет качаться медленнее, так как там слабее гравитация и меньше значение ускорения свободного падения.

Указанное приближение является корректным только при небольших углах отклонения, поскольку выражение для углового ускорения пропорционально синусу координаты:

$\ell m g \sin\theta=I \alpha,$

где

I — момент инерции; в данном случае I = m ℓ 2.

Когда угол θ мал, можно считать, что sin θ ≈ θ, и выражение принимает вид:

$\ell m g \theta=I \alpha$

что делает угловое ускорение прямо пропорциональным углу θ, а это удовлетворяет определению простого гармонического движения.

Затухающий гармонический осциллятор

Взяв за основу ту же модель, добавим в неё силу вязкого трения. Сила вязкого трения направлена против скорости движения груза относительно среды и пропорциональна этой скорости. Тогда полная сила, действующая на груз, записывается так:

$F = -k x - \alpha v \,$

Проводя аналогичные действия, получаем дифференциальное уравнение, описывающее затухающий осциллятор:

$\ddot x + 2 \gamma \dot x + \omega_0^2 x = 0$

Здесь введено обозначение: $2 \gamma = \frac{\alpha }{ m}$ . Коэффициент $\gamma$ носит название постоянной затухания. Он тоже имеет размерность частоты.

Решение же распадается на три случая.

При малом трении ( $\gamma < \omega_0$ ) общее решение записывается в виде:

$x(t) = A e^{-\gamma t} sin(\omega_f t + \varphi)$ , где $\omega_f = \sqrt{\omega_0^2 - \gamma^2}$ — частота свободных колебаний.

Затухание $\gamma = \omega_0$ называют критическим. Начиная с такого значения показателя затухания, осциллятор будет совершать так называемое неколебательное движение. В граничном случае движение происходит по закону:

$\ x(t) = (A + B t)e^{-\gamma t}$

При сильном же трении $\gamma > \omega_0$ решение выглядит следующим образом:

$x(t) = A e^{-\beta_1 t} + B e^{-\beta_2 t}$ , где $\beta_{1,2}=\gamma \pm \sqrt{\gamma^2 - \omega_0^2}$

Критическое затухание примечательно тем, что именно при критическом затухании осциллятор быстрее всего стремится в положение равновесия. Если трение меньше критического, он дойдёт до положения равновесия быстрее, однако «проскочит» его по инерции, и будет совершать колебания. Если трение больше критического, то осциллятор будет экспоненциально стремиться к положению равновесия, но тем медленнее, чем больше трение.

Поэтому в стрелочных индикаторах (например, в амперметрах) обычно стараются ввести именно критическое затухание, чтобы прочитать его показания можно было максимально быстро.

Затухание осциллятора также часто характеризуют безразмерным параметром, называемым добротностью. Добротность обычно обозначают буквой . По определению, добротность равна:

$Q = \frac{\omega_0}{2 \gamma}$

Чем больше добротность, тем медленнее затухают колебания осциллятора.

У осциллятора с критическим затуханием добротность равна 0,5. Соответственно, добротность указывает характер поведения осциллятора. Если добротность больше 0,5, то свободное движение осциллятора представляет собой колебания; со временем он пересечёт положение равновесия неограниченное количество раз. Добротность, меньшая или равная 0,5, соответствует неколебательному движению осциллятора; в свободном движении он пересечёт положение равновесия не более одного раза.

Добротность иногда называют коэффициентом усиления осциллятора, так как при некоторых способах возбуждения при совпадении частоты возбуждения с резонансной амплитуда колебаний оказывается примерно в раз больше, чем при возбуждении на низкой частоте.

Также добротность примерно равна количеству колебательных циклов, за которое амплитуда колебаний уменьшается в раз, умноженному на $\pi$ .

В случае колебательного движения затухание ещё характеризуют такими параметрами, как:

Время жизни колебаний (оно же время затухания, оно же время релаксации) τ — время, за которое амплитуда колебаний уменьшится в e раз.

$\tau=1 / \gamma.$

Это время рассматривается как время, необходимое для затухания (прекращения) колебаний (хотя формально свободные колебания продолжаются бесконечно долго).

Логарифмический декремент затухания. Определяется как логарифм отношения двух последовательных максимальных отклонений в одну сторону: $d = \operatorname{ln} ( x_{max \; n} / x_{max \; n+1} ).$ Величина, обратная d, есть количество колебаний, которое пройдёт за время затухания τ.

Вынужденные колебания

Колебания осциллятора называют вынужденными, когда на него производится некоторое дополнительное воздействие извне. Это воздействие может производиться различными средствами и по различным законам. Например, силовым возбуждением называется воздействие на груз силой, зависящей только от времени по определённому закону. Кинематическим возбуждением называют воздействие на осциллятор движением точки закрепления пружины по заданному закону. Возможно также воздействие трением, когда, например, среда, с которой груз испытывает трение, совершает движение по заданному закону.

Литература

Бутиков Е. И. Собственные колебания линейного осциллятора. Учебное пособие

См. также

Примечания

↑ Решение приведённого дифференциального уравнения можно записать с помощью функции синуса:
$x(t) = A\sin(\omega t +\varphi)$
И это тоже верное решение, поскольку известно общее равенство cos θ = sin(π/2 — θ). Используя тригонометрические соотношения, можно записать
$A\cos(\omega t +\varphi) = A\cos(\varphi)\cos(\omega t)-A\sin(\varphi)\sin(\omega t),$
и таким образом
$a\cos(\omega t) + b\sin(\omega t)$
также является верным решением при соответствующим образом выбранных постоянных a и b.
↑ Максимальное перемещение (то есть амплитуда), x_max, имеет место, когда cos(ω_t + φ) = 1, и таким образом, когда x_max = A. Таким образом, A является амплитудой.
Поскольку
$\cos(\omega t + \varphi) = \cos(\omega t + 2\pi + \varphi) = \cos(\omega(t + 2\pi/\omega) + \varphi),$
то величина 2π/ω является периодом T (время, за которое совершается одно полное колебание). Также, поскольку T = 1/f, ω = 2π_f является угловой скоростью.