Нечёткая логика | это... Что такое Нечёткая логика? (original) (raw)

Нечёткая логика (англ. fuzzy logic) и теория нечётких множеств — раздел математики, являющийся обобщением классической логики и теории множеств. Понятие нечёткой логики было впервые введено профессором Лютфи Заде в 1965 году. В его статье понятие множества было расширено допущением, что функция принадлежности элемента к множеству может принимать любые значения в интервале [0...1], а не только 0 или 1. Такие множества были названы нечёткими. Также автором были предложены различные логические операции над нечёткими множествами и предложено понятие лингвистической переменной, в качестве значений которой выступают нечёткие множества.

Предметом нечёткой логики является построение моделей приближенных рассуждений человека и использование их в компьютерных системах[1].

Содержание

Направления исследований нечёткой логики

В настоящее время существует по крайней мере два основных направления научных исследований в области нечёткой логики:

Математические основы

Символическая нечёткая логика

Символическая нечёткая логика основывается на понятии t-нормы. После выбора некоторой t-нормы (а её можно ввести несколькими разными способами) появляется возможность определить основные операции над пропозициональными переменными: конъюнкцию, дизъюнкцию, импликацию, отрицание и другие.

Нетрудно доказать теорему о том, что дистрибутивность, присутствующая в классической логике, выполняется только в случае, когда в качестве t-нормы выбирается t-норма Гёделя.

Кроме того, в силу определенных причин, в качестве импликации чаще всего выбирают операцию, называемую residium (она, вообще говоря, также зависит от выбора t-нормы).

Определение основных операций, перечисленных выше, приводит к формальному определению базисной нечёткой логики, которая имеет много общего с классической булевозначной логикой (точнее, с исчислением высказываний).

Существуют три основных базисных нечётких логики: логика Лукасевича, логика Гёделя и вероятностная логика (англ. product logic). Интересно, что объединение любых двух из трёх перечисленных выше логик приводит к классической булевозначной логике.

Теория приближенных вычислений

Основное понятие нечёткой логики в широком смысле — нечёткое множество, определяемое при помощи обобщенного понятия характеристической функции. Затем вводятся понятия объединения, пересечения и дополнения множеств (через характеристическую функцию; задать можно различными способами), понятие нечёткого отношения, а также одно из важнейших понятий — понятие лингвистической переменной.

Вообще говоря, даже такой минимальный набор определений позволяет использовать нечёткую логику в некоторых приложениях, для большинства же необходимо задать ещё и правило вывода (и оператор импликации).

Нечеткая логика и нейронные сети

Поскольку нечеткие множества описываются функциями принадлежности, а t-нормы и k-нормы обычными математическими операциями, можно представить нечеткие логические рассуждения в виде нейронной сети. Для этого функции принадлежности надо интерпретировать как функции активации нейронов, передачу сигналов как связи, а логические t-нормы и k-нормы, как специальные виды нейронов, выполняющие математические соответствующие операции. Существует большое разнообразие подобных нейро-нечетких сетей neuro-fuzzy network (англ.) . Например, ANFIS ( Adaptive Neuro fuzzy Inference System) - адаптивная нейро-нечеткая система вывода.[2] (англ.)

Она может быть описана в универсальной форме аппроксиматоров как

y(x)=\sum^{N}_{i=1} \phi_i(x)*\theta_i ,

кроме того, этой формулой могут быть описаны также некоторые виды нейронных сетей, такие как радиально базисные сети (RBF), многослойные персептроны (MLP), а также вейвлеты и сплайны.

Примеры

Нечёткое множество, содержащее число 5

Нечёткое множество, содержащее число 5, можно задать, например, такой характеристической функцией: \mu_A \left( x \right) = \left( 1+\left| x - 5 \right| ^ n \right) ^{-1}

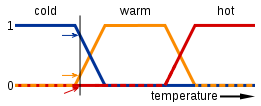
Пример определения лингвистической переменной

В обозначениях, принятых для лингвистической переменной:

Fuzzy logic temperature en.svg

Характеристические функции:

Правило G порождает новые термы с использованием союзов «и», «или», «не», «очень», «более или менее».

См. также

Примечания

  1. ↑ В. В. Круглов, M. И. Дли, Р. Ю. Голунов. Нечеткая логика и искусственные нейронные сети. — М.: Физматлит, 2000. — 224 с. ISBN 5-94052-027-8.
  2. ↑ Jang, J.-S. R., "ANFIS: Adaptive-Network-based Fuzzy Inference Systems," IEEE Transactions on Systems, Man, and Cybernetics, Vol. 23, No. 3, pp. 665-685, May 1993.

Литература

Ссылки

Просмотр этого шаблона Инженерия знаний
Общие понятия Данные · Метаданные · Знания · Метазнание · Представление знаний · База знаний · Онтология · Семантическая паутина
Жёсткие модели Продукции · Семантические сети · Фреймы · Логическая модель
Мягкие методы Нейросети · Эволюционное моделирование · Нечёткая логика
Применения Экспертные системы · Интеллектуальный анализ данных · Извлечение информации · Виртуальные собеседники · Гибридные интеллектуальные системы
Искусственный интеллект · Машинное обучение · Обработка естественного языка