Октамино | это... Что такое Октамино? (original) (raw)

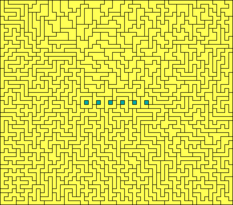
369 свободных октамино

Октамино — полимино 8-го порядка, то есть плоская фигура, состоящая из восьми равных квадратов, соединённых сторонами. С фигурами октамино, как со всеми полимино, связано много задач занимательной математики.

Если не считать различными фигуры, совпадающие при поворотах и зеркальных отражениях, то различных («свободных») форм октамино насчитывается 369 (см.рисунок)[1]. Существует 704 видов «односторонних» октамино (если зеркальные отражения считаются различными фигурами) и 2725 видов «фиксированных» октамино (различными считаются также и повороты).[2]

Классификация фигур октамино по свойствам симметрии

369 свободных фигур октамино по их свойствам симметрии можно разделить на 8 категорий:

316 фигур октамино (на рисунке изображены серым цветом) асимметричны;
23 октамино (изображены красным) имеют ось симметрии, параллельную линиям квадратной сетки;
5 октамино (изображены зелёным) имеют диагональную ось симметрии;
18 октамино (изображены синим) имеют центральную (вращательную) симметрию второго порядка;
1 октамино (изображено жёлтым) имеют центральную (вращательную) симметрию четвёртого порядка;
4 октамино (изображены фиолетовым) имеют две оси симметрии, параллельных линиям сетки;
1 октамино (изображено оранжевым) имеет две диагональных оси симметрии.
1 октамино (изображено сине-зелёным) имеет четыре оси симметрии — две параллельных линиям сетки и две диагональных.

Октамино — наименьший порядок полимино, в котором реализуются все восемь возможных типов симметрии. Следующий порядок полимино с этим свойством — додекамино (двенадцатиклеточное полимино).

Если зеркальные отражения фигур считать различными, то первая, четвёртая и пятая категории удваиваются в численности, что даёт дополнительно 335 октамино, то есть в общей сложности 704 односторонних октамино.

Если повороты также рассматривать как различные фигуры, то

фигуры первой категории могут быть ориентированы восемью различными способами;
фигуры из категорий со второй по четвёртую — четырьмя;
фигуры из категорий с пятой по седьмую — двумя;
единственная фигура из последней категории может быть ориентирована единственным образом.

Это даёт $316 \times 8 + (23 + 5 + 18) \times 4 + (1 + 4 + 1)\times 2 + 1 = 2725$ фиксированных октамино.

Составление фигур из октамино

Октамино с отверстиями

Укладка октамино в прямоугольник 51×58 с 6 отверстиями

Укладка октамино в три прямоугольника 29×34, каждый с двумя отверстиями

Среди 369 свободных октамино есть 6 фигур с отверстиями («неодносвязные»). Из этого следует, что сплошное покрытие какого-либо прямоугольника площадью $369\times8=2952$ квадратов полным набором октамино невозможно. Однако они могут быть уложены в некоторые прямоугольники площадью 2958 квадратов с шестью одноклеточными отверстиями. Поскольку число 2958 представляет собою произведение простых множителей 2×3×17×29, то можно поставить вопрос о составлении прямоугольников 6×493, 17×174, 29×102, 34×87 и 51×58.

Для прямоугольника 51×58 существует решение с симметричным расположением отверстий, представленное на рисунке. Существует также укладка октамино в три прямоугольника 29×34, каждый с двумя отверстиями вблизи центра. Комбинируя их различными способами, можно получить прямоугольник 34×87 или 29×102 с симметричным расположением трёх пар отверстий. Решения для прямоугольников 6×493 и 17×174 пока не известны.

Примечания

↑ Голомб С. В. Полимино. — Пер. с англ. В.Фирсова. — М.: Мир, 1975. — 207 с., ил.
↑ Octomino — from Wolfram MathWorld

Полиформы
Полимино	Домино · Тримино · Тетрамино · Пентамино · Гексамино · Гептамино · Октамино · Нонамино
Другие	Connect (игра) · Полиаболо · Поликуб · Полидрафтер · Полигекс · Полиамонд · Полиоминоид · Полистик