Многочлены Чебышёва | это... Что такое Многочлены Чебышёва? (original) (raw)

Многочле́ны Чебышёва — две последовательности многочленов T n(x) и U n(x), 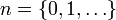$n=\{0,1,\dots\}$ названные в честь Пафнутия Львовича Чебышёва.
Многочлены Чебышёва играют важную роль в теории приближений, поскольку корни многочленов Чебышёва первого рода используются в качестве узлов в интерполяции алгебраическими многочленами.

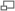
Многочлены Чебышёва первого рода

Многочлен Чебышёва первого рода T n(x) характеризуется как многочлен степени n со старшим коэффициентом 2_n_ - 1, который меньше всего отклоняется от нуля на интервале [ − 1,1]. Впервые рассмотрены самим Чебышёвым.

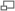
Многочлены Чебышёва второго рода

Многочлен Чебышёва второго рода U n(x) характеризуется как многочлен степени n со старшим коэффициентом 2_n_, интеграл от абсолютной величины которого по интервалу [ − 1,1] принимает наименьшее возможное значение. Впервые рассмотрены в совместной работе двух учеников Чебышёва — Коркина и Золотарёва.

Рекурсивное определение

Многочлены Чебышёва первого рода T n(x) могут быть определены с помощью рекуррентного соотношения:

$T_0(x) = 1 \,$

$T_1(x) = x \,$

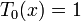
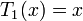
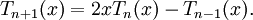
$T_{n+1}(x) = 2xT_n(x) - T_{n-1}(x). \,$

Многочлены Чебышёва второго рода U n(x) могут быть определены с помощью рекуррентного соотношения:

$U_0(x) = 1 \,$

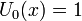
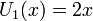
$U_1(x) = 2x \,$

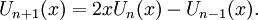
$U_{n+1}(x) = 2xU_n(x) - U_{n-1}(x). \,$

Явные формулы

Многочлены Чебышёва являются решениями уравнения Пелля:

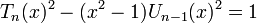
$T_n(x)^2 - (x^2-1) U_{n-1}(x)^2 = 1\,$

в кольце многочленов с вещественными коэффициентами и удовлетворяют тождеству:

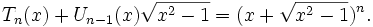
$T_n(x) + U_{n-1}(x)\sqrt{x^2-1} = (x + \sqrt{x^2-1})^n.$

Из последнего тождества также следуют явные формулы:

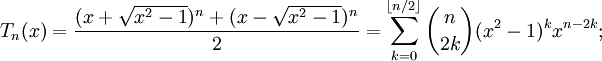
$T_n(x)=\frac{(x+\sqrt{x^2-1})^n+(x-\sqrt{x^2-1})^n}{2} = \sum_{k=0}^{\lfloor n/2\rfloor} \binom{n}{2k} (x^2-1)^k x^{n-2k};$

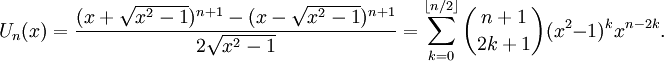
$U_n(x)=\frac{(x+\sqrt{x^2-1})^{n+1}-(x-\sqrt{x^2-1})^{n+1}}{2\sqrt{x^2-1}} = \sum_{k=0}^{\lfloor n/2\rfloor} \binom{n+1}{2k+1} (x^2-1)^k x^{n-2k}.$

Тригонометрическое определение

Многочлены Чебышёва первого рода 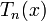$T_n(x)\,$ могут быть также определены с помощью равенства:

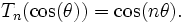
$T_n(\cos(\theta))=\cos(n\theta). \,$

или, что почти эквивалентно,

$T_n(z)=\cos(n \arccos(z))\,$

Многочлены Чебышёва второго рода U n(x) могут быть также определены с помощью равенства:

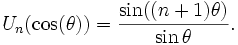
$U_n(\cos(\theta)) = \frac{\sin((n+1)\theta)}{\sin\theta}.$

Примеры

Несколько первых многочленов Чебышёва первого рода

$T_0(x) = 1 \,$

$T_1(x) = x \,$

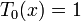
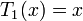
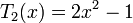
$T_2(x) = 2x^2 - 1 \,$

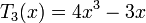
$T_3(x) = 4x^3 - 3x \,$

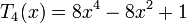
$T_4(x) = 8x^4 - 8x^2 + 1 \,$

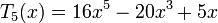
$T_5(x) = 16x^5 - 20x^3 + 5x \,$

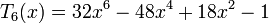
$T_6(x) = 32x^6 - 48x^4 + 18x^2 - 1 \,$

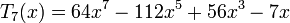
$T_7(x) = 64x^7 - 112x^5 + 56x^3 - 7x \,$

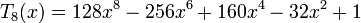
$T_8(x) = 128x^8 - 256x^6 + 160x^4 - 32x^2 + 1 \,$

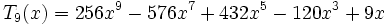
$T_9(x) = 256x^9 - 576x^7 + 432x^5 - 120x^3 + 9x \,$

Несколько первых многочленов Чебышёва второго рода

$U_0(x) = 1 \,$

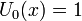
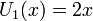
$U_1(x) = 2x \,$

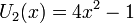
$U_2(x) = 4x^2 - 1 \,$

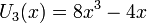
$U_3(x) = 8x^3 - 4x \,$

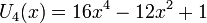
$U_4(x) = 16x^4 - 12x^2 + 1 \,$

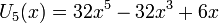
$U_5(x) = 32x^5 - 32x^3 + 6x \,$

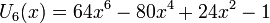
$U_6(x) = 64x^6 - 80x^4 + 24x^2 - 1 \,$

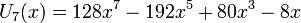
$U_7(x) = 128x^7 - 192x^5 + 80x^3 - 8x \,$

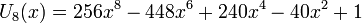
$U_8(x) = 256x^8 - 448 x^6 + 240 x^4 - 40 x^2 + 1 \,$

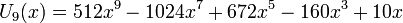
$U_9(x) = 512x^9 - 1024 x^7 + 672 x^5 - 160 x^3 + 10 x \,$

Свойства

Многочлены Чебышёва обладают следующими свойствами:

T n(1) = 1	T n( − 1) = ( − 1)n	T_2_n(0) = ( − 1)n	T_2_n + 1(0) = 0
U n(1) = n + 1	U_2_n(0) = ( − 1)n	U_2_n + 1(0) = 0

Вариации и обобщения

Вопрос о многочленах минимальной нормы с фиксированными коэффициентами при двух старших степенях был рассмотрен позднее Золотарёвым, найденные им полиномы носят название многочлены Золотарёва.
многочлены Фабера

Ссылки

Васильев Н., Зелевинский А. Многочлены Чебышёва и рекуррентные соотношения // Квант. — 1982. — № 1. — С. 12-19.
Сайт, посвящённый методу дискретных особенностей в задачах математической физики, который основан на интерполяционных формулах с использованием полиномов Чебышёва

Литература

Кампе де Ферье Ж., Кемпбелл Р., Петьо Г., Фогель Т. Функции математической физики. — М.: Физматлит, 1963.

Ортогональные многочлены
Многочлены Бернштейна-Сеге • Многочлены Бесселя • Многочлены Гегенбауера • Многочлены Гейне-Ахиезера • Многочлены Лагерра • Многочлены Лежандра • Многочлены Полачека • Многочлены Чебышёва • [Многочлены Эрмита]] • Многочлены Якоби

Ортогональные многочлены

Многочлены Бернштейна-Сеге • Многочлены Бесселя • Многочлены Гегенбауера • Многочлены Гейне-Ахиезера • Многочлены Лагерра • Многочлены Лежандра • Многочлены Полачека • Многочлены Чебышёва • [Многочлены Эрмита]] • Многочлены Якоби