Градиентный спуск | это... Что такое Градиентный спуск? (original) (raw)

Градиентный спуск — метод нахождения локального экстремума (минимума или максимума) функции с помощью движения вдоль градиента. Для минимизации функции в направлении градиента используются методы одномерной оптимизации, например, метод золотого сечения. Также можно искать не наилучшую точку в направлении градиента, а какую-либо лучше текущей.

Наиболее простой в реализации из всех методов локальной оптимизации. Имеет довольно слабые условия сходимости, но при этом скорость сходимости достаточно мала (линейна). Шаг градиентного метода часто используется как часть других методов оптимизации, например, метод Флетчера - Ривса.

Описание

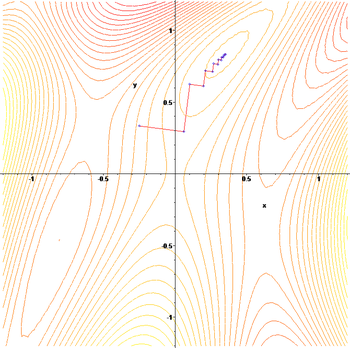
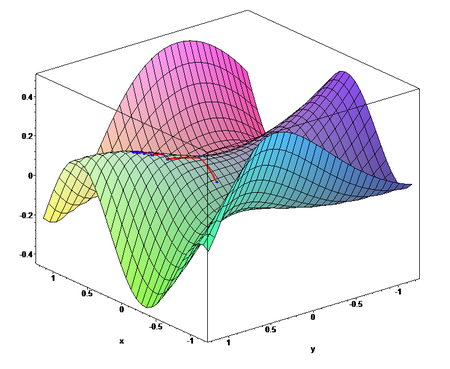
Иллюстрация последовательных приближений к точке экстремума в направлении наискорейшего спуска (красн.) в случае дробного шага. Синим отмечены линии уровня.

Пусть целевая функция имеет вид:

$F(\vec{x}):\;\mathbb{X}\to\mathbb{R}$ .

И задача оптимизации задана следующим образом:

$F(\vec{x})\to\min_{\vec{x}\in\mathbb{X}}\!$

Основная идея метода заключается в том, чтобы идти в направлении наискорейшего спуска, а это направление задаётся антиградиентом $-\nabla F$ :

$\overrightarrow{x}^{[j+1]}=\overrightarrow{x}^{[j]}-\lambda^{[j]}\nabla F(\overrightarrow{x}^{[j]}) \!$

где $\lambda^{[j]}$ выбирается

постоянной, в этом случае метод может расходиться;
дробным шагом, т.е. длина шага в процессе спуска делится на некое число;
наискорейшим спуском: $\lambda^{[j]}=\mathrm{argmin}_{\lambda} \,F(\vec{x}^{[j]}-\lambda^{[j]}\nabla F(\vec{x}^{[j]})) \!$

Алгоритм

Задают начальное приближение и точность расчёта $\vec{x}^0, \quad \varepsilon$
Рассчитывают $\overrightarrow{x}^{[j+1]}=\overrightarrow{x}^{[j]}-\lambda^{[j]}\nabla F(\overrightarrow{x}^{[j]}) \!$ , где $\lambda^{[j]}=\mathrm{argmin}_{\lambda} \,F(\vec{x}^{[j]}-\lambda^{[j]}\nabla F(\vec{x}^{[j]})) \!$
Проверяют условие остановки:

Соотношение Канторовича

Для квадратичной функции вида $\frac{x^T \Gamma x }{2} + c^T x, \Gamma^T=\Gamma$ метод наискорейшего градиентного поиска сходится из любой начальной точки x_0 со скоростью геометрической прогрессии (линейно) со знаменателем, не превосходящим значение . При этом справедливы следующие оценки:

$\exists a=a(x_0), T>0: 0 \le a \le q = \frac{\left ( \lambda_{min} / \lambda_{max} - 1 \right )^2}{\left ( \lambda_{min} / \lambda_{max} + 1 \right )^2}$ ,

$f(x_k)<f(x^*) \le a^k (f(x_0)-f(x^*))$ ,

$\|x_k - x^* \| \le T a^{k/2} \| x_0 - x^* \|$ ,

где $\lambda_{min}$ и $\lambda_{max}$ - минимальное и максимальное собственные числа числа матрицы вторых производных $\nabla^2 f(x) = \Gamma$ .

Таким образом, поскольку функция близка в малом к своей квадратичной аппроксимации, скорость сходимости, в окрестности точки минимума, зависит от отношения собственных чисел. Чем больше это отношение, тем хуже сходимость метода.

Пример

Применим градиентный метод к функции $F(x,y)=\sin\left(\frac{1}{2} x^2 - \frac{1}{4} y^2 + 3 \right) \cos(2 x+1-e^y)$ . Тогда последовательные приближения будут выглядеть так:

Усовершенствование

Метод градиентного спуска оказывается очень медленным при движении вдоль оврага ( см. овражные функции). Примером такой функции является функции Розенброка. Более эффективным считается метод сопряжённых градиентов.

Ссылки

J. Mathews. Module for Steepest Descent or Gradient Method.

Литература

Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов. — М.: Высш. шк., 1986.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.
Коршунов Ю.М., Коршунов Ю.М. Математические основы кибернетики. — М.: Энергоатомиздат, 1972.
Максимов Ю.А.,Филлиповская Е.А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
Максимов Ю.А. Алгоритмы линейного и дискретного программирования. — М.: МИФИ, 1980.
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.
С. Ю. Городецкий, В. А. Гришагин. Нелинейное программирование и многоэкстремальная оптимизация. — Нижний Новгород: Издательство Нижегородского Университета, 2007. — С. 357-363.

Методы оптимизации
Одномерные	Метод золотого сечения • Дихотомия • Метод парабол • Перебор по сетке • Метод Фибоначчи • Троичный поиск
Прямые методы	Метод Гаусса • Метод Нелдера — Мида • Метод Хука — Дживса • Метод конфигураций • Метод Розенброка
Первого порядка	Градиентный спуск • Метод Зойтендейка • Покоординатный спуск • Метод сопряжённых градиентов • Квазиньютоновские методы • Алгоритм Левенберга — Марквардта
Второго порядка	Метод Ньютона • Метод Ньютона — Рафсона
Стохастические	Метод Монте-Карло • Имитация отжига • Эволюционные алгоритмы • Дифференциальная эволюция • Муравьиный алгоритм • Метод роя частиц
Методы линейного программирования	Симплекс-метод • Алгоритм Гомори • Метод эллипсоидов • Метод потенциалов
Методы нелинейногопрограммирования	Последовательное квадратичное программирование