Псевдоскалярное произведение | это... Что такое Псевдоскалярное произведение? (original) (raw)

Псевдоскалярным[1] или косым произведением векторов  и
и  на плоскости называется число
на плоскости называется число

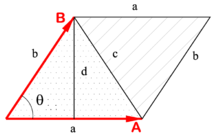
где  — угол вращения (против часовой стрелки) от
— угол вращения (против часовой стрелки) от  к
к  . Если хотя бы один из векторов
. Если хотя бы один из векторов  и
и  нулевой, то полагают
нулевой, то полагают  . Геометрически псевдоскалярное произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора. С её помощью удобно работать с площадями многоугольников, выражать условия коллинеарности векторов и находить углы между ними.
. Геометрически псевдоскалярное произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора. С её помощью удобно работать с площадями многоугольников, выражать условия коллинеарности векторов и находить углы между ними.
Псевдоскалярное произведение существует только для 2-мерных векторов, его аналогом в трехмерном пространстве является тройное скалярное произведение.
Свойства
где « » и «
» и « » соответственно — векторное и скалярное произведение, а
» соответственно — векторное и скалярное произведение, а  — единичный вектор нормали к плоскости. Знак плюс берется в случае, если правый базис на плоскости, дополненный вектором
— единичный вектор нормали к плоскости. Знак плюс берется в случае, если правый базис на плоскости, дополненный вектором  , образует также правый базис; в противном случае минус.
, образует также правый базис; в противном случае минус.

- Это выражение также можно записать через символ Леви-Чивиты в двумерном пространстве:

См. также
Ссылки
- ↑ Прасолов В. В., Задачи по планиметрии. — 4-е изд., дополненное — М.: МЦНМО, 2001. — 584 с. ; ISBN 5-900916-82-0.