Проектор (алгебра) | это... Что такое Проектор (алгебра)? (original) (raw)

У этого термина существуют и другие значения, см. Проектор.

В линейной алгебре и функциональном анализе линейный оператор P, действующий в линейном пространстве, называется прое́ктором (а также опера́тором проекти́рования и проекцио́нным опера́тором) если _P_2 = P. Иногда проекционный оператор называют идемпотентным.

Несмотря на свою абстрактность, это определение обобщает идею построения геометрической проекции.

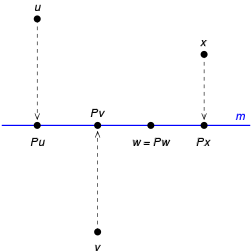
В качестве определения можно использовать следующее свойство проектора: линейный оператор 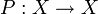$P:X\to X$ является проектором, если и только если существуют такие подпространства U и V пространства X, что X раскладывается в их прямую сумму, и при этом для любого элемента 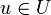$u\in U$ имеем P u = u, а для любого элемента 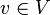$v\in V$ имеем P v = 0. Подпространство U называется образом, а V — ядром проектора P.

В общем случае, разложение линейного пространства в прямую сумму неединственно. Поэтому, для подпространства V пространства X, вообще говоря, существует много проекторов, образ или ядро которого совпадает с V.

Свойства проекционных операторов

Пусть I — тождественный оператор. Если P - проектор, то I − P - тоже проектор, причём ker_I_ − P = Im_P_ и Im_I_ − P = ker_P_.
В конечномерном нормированном пространстве все проекционные операторы непрерывны.
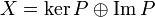Для банахова же пространства проекционный оператор будет непрерывным, если его образ замкнут, при этом ядро проектора тоже окажется замкнутым. Таким образом, непрерывный проектор задаёт разложение пространства в прямую сумму замкнутых подпространств: $X=\ker P \oplus \mathrm{Im}\, P$ .
Собственными значениями проектора могут быть только 0 и 1. Соответствующими собственными подпространствами проектора будут его ядро и образ.

Комбинации проекторов

Пусть _P_1 и _P_2 проекторы заданные на пространстве X и проектирующие на подпространства _M_1 и _M_2 соответственно. Тогда

Примеры

Ортогональная проекция (смотрите ниже) точек (x, y, z) пространства _R_3 на плоскость Oxy задаётся матрицей

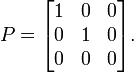
$P = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix}.$

Действует на точки она следующим образом:

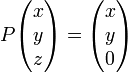
$P \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x \\ y \\ 0 \end{pmatrix}$

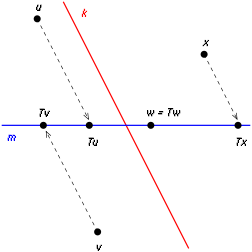
Преобразование T является косоугольной проекцией вдоль k на прямую m. _U_=m и _V_=k.

Простейший неортогональный проектор осуществляет косоугольную проекцию точек плоскости на прямую. Он задаётся матрицей:

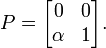
$P = \begin{bmatrix} 0 & 0 \\ \alpha & 1 \end{bmatrix}.$

Легко показать, что это действительно проектор:

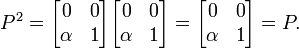
$P^2 = \begin{bmatrix} 0 & 0 \\ \alpha & 1 \end{bmatrix} \begin{bmatrix} 0 & 0 \\ \alpha & 1 \end{bmatrix} = \begin{bmatrix} 0 & 0 \\ \alpha & 1 \end{bmatrix} = P.$

Проекция, задаваемая P, ортогональна, если и только если α = 0.

Ортогональный проектор

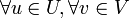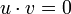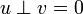Если пространство X - гильбертово, то есть обладает скалярным произведением (а значит и понятием ортогональности), то можно ввести понятие ортогональный проектор. Ортогональный проектор — это частный случай проектора, когда выше упомянутые подпространства U и V ортогональны друг другу, иными словами, когда $\forall u\in U, \forall v\in V$ (u,v) = 0, или $u\cdot v =0$ , или $u\perp v =0$ . В этом случае проекция элемента $x\in X$ является ближайшим к нему элементом пространства U.

Литература

Треногин В. А. Функциональный анализ. — М.: Наука, 1980. — 495 с.
Халмош П. Конечномерные векторные пространства = Finite-dimensional vector spaces. — М.: Физматгиз, 1963. — 264 с.