Инверсия (геометрия) | это... Что такое Инверсия (геометрия)? (original) (raw)

У этого термина существуют и другие значения, см. Инверсия.

Инверсия (от лат. inversio — обращение) относительно окружности есть преобразование евклидовой плоскости, переводящее обобщённые окружности (окружности либо прямые) в обобщённые окружности, при котором одна из окружностей поточечно переводится в себя.

Содержание

1 Определение
2 Свойства
3 Построение
4 Координатные представления
- 4.1 Декартовы координаты
- 4.2 Полярные координаты
5 Применение
6 Примечания
7 Ссылки

Определение

Инверсия

Пусть в евклидовой плоскости задана некоторая окружность $\Gamma$ с центром (называемым полюсом или центром инверсии, эта точка выколота) и радиусом . Инверсия точки относительно $\Gamma$ есть точка , лежащая на луче такая, что

$|OP'|\cdot|OP|=R^2.$

Инверсия переводит внутреннюю область окружности во внешнюю, и обратно.

Часто к плоскости добавляют «бесконечно удалённую точку» $\infty$ и считают её инверсным образом , а — инверсным образом $\infty$ . В этом случае, инверсия является биективным преобразованием этой расширенной «круговой плоскости».

Аналогично определяется инверсия евклидова пространства относительно сферы и инверсия в евклидовых пространствах более высоких размерностей.

Свойства

Образ центра окружности не является центром образа

Инверсия относительно окружности $\Gamma$ с центром O обладает следующими основными свойствами:

Инверсия является инволюцией: если точка P переходит в точку Q, то и точка Q переходит в точку P.
Прямая, проходящая через O, переходит в себя.
Прямая, не проходящая через O, переходит в окружность, проходящую через O с выколотой точкой O; и обратно, окружность, проходящая через O, переходит в прямую, не проходящую через O.
Окружность, не проходящая через O, переходит в окружность, не проходящую через O (при этом образ её центра не является центром образа).
Инверсия является конформным отображением второго рода (т. е. она сохраняет углы между кривыми и меняет ориентацию).
Окружность или прямая, перпендикулярная к $\Gamma$ , переходит в себя.

Построение

Построение образа точки при инверсии относительно окружности

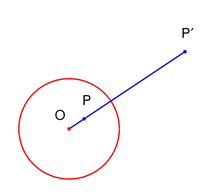
Получить образ P' точки P при инверсии относительно данной окружности с центром O можно следующим образом[1]:

Если расстояние от P до O больше радиуса окружности — провести из P касательную к окружности, тогда перпендикуляр к прямой OP из точки касания пересечёт эту прямую в искомой точке P'
Если расстояние от P до O меньше радиуса окружности — провести через P перпендикуляр к OP, а через точку его пересечения с окружностью — касательную к ней, которая пересечёт OP в искомой точке P'
Если расстояние от P до O равно радиусу окружности, образ P совпадёт с ней самой

Координатные представления

Декартовы координаты

Инверсия относительно единичной окружности с центром в начале координат задаётся соотношением

$(x,y)\mapsto \left(\frac{x}{x^2+y^2},\frac{y}{x^2+y^2}\right)$ .

Если точку плоскости задать одной комплексной координатой z=x+iy , то это выражение можно представить в виде

$z\mapsto (\bar z)^{-1}$ ,

где $\bar z$ — комплексно сопряжённое число для . Данная функция комплексного переменного является антиголоморфной, откуда, в частности, следует конформность инверсии.

В общем случае, инверсия относительно окружности с центром в точке O=(x_0,y_0) и радиусом задаётся соотношением

$(x,y)\mapsto \left(x_0+\frac{r^2(x-x_0)}{(x-x_0)^2+(y-y_0)^2},y_0+\frac{r^2(y-y_0)}{(x-x_0)^2+(y-y_0)^2}\right)$ .

Полярные координаты

Инверсия относительно окружности радиуса с центром в начале координат задаётся соотношением

$(\phi,\rho)\mapsto (\phi,r^2/\rho)$ .

Применение

С помощью инверсии можно решить известную задачу Аполлония, математически описать принцип действия механизма Липкина — Посселье.

Примечания

↑ Погорелов А. В. Геометрия. — М.: Наука, 1983. — С. 41—42. — 288 с.

Ссылки

	Инверсия (геометрия) на Викискладе?

Ануфриенко С. А. Симметрия относительно окружности.
Бакельман И. Я. Инверсия. Популярные лекции по математике, Вып. 44, М., Наука, 1966.
Жижилкин И. Д. Инверсия. М.: МЦНМО, 2009.
Курант Р., Роббинс Г. Что такое математика?. Гл. III, § 4.