Двойной факториал | это... Что такое Двойной факториал? (original) (raw)

Факториа́л числа n (обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел до n включительно:

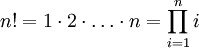$n! = 1\cdot 2\cdot\ldots\cdot n =\prod_{i=1}^n i$ .

По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.

Эта функция часто используется в комбинаторике, теории чисел и функциональном анализе.

Иногда словом «факториал» неформально называют восклицательный знак.

Свойства

Комбинаторное определение

В комбинаторике факториал определяется как количество перестановок множества из n элементов. Например, элементы множества {A,B,C,D} можно линейно упорядочить 4!=24 способами:

ABCD BACD CABD DABC ABDC BADC CADB DACB ACBD BCAD CBAD DBAC ACDB BCDA CBDA DBCA ADBC BDAC CDAB DCAB ADCB BDCA CDBA DCBA

Связь с гамма-функцией

Факториал связан с гамма-функцией от целочисленного аргумента соотношением:

n! = Γ(n + 1)

Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел. Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при 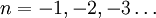$n=-1, -2, -3\ldots$ .

Формула Стирлинга

Формула Стирлинга — асимптотическая формула для вычисления факториала:

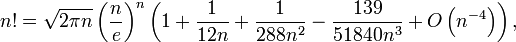
$n! = \sqrt{2\pi n}\left(\frac{n}{e}\right)^n \left(1 + \frac{1}{12 n} + \frac{1}{288 n^2} - \frac{139}{51840 n^3}+O\left(n^{-4}\right)\right),$

см. O-большое. Коэффициенты этого разложения дают последовательность A001163 в OEIS (числители) и последовательность A001164 в OEIS (знаменатели).

Во многих случаях для приближенного значения факториала достаточно рассматривать только главный член формулы Стирлинга:

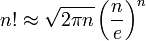
$n! \approx \sqrt{2\pi n}\left(\frac{n}{e}\right)^n$

При этом можно утверждать, что

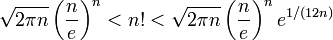
$\sqrt{2\pi n}\left(\frac{n}{e}\right)^n < n! < \sqrt{2\pi n}\left(\frac{n}{e}\right)^n e^{1/(12n)}$

Разложение на простые числа

Каждое простое число p входит в разложение n! на простые в степени

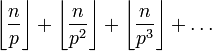
$\left\lfloor \frac{n}{p}\right\rfloor + \left\lfloor \frac{n}{p^2}\right\rfloor + \left\lfloor \frac{n}{p^3}\right\rfloor + \ldots$

Таким образом,

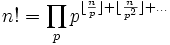$n! = \prod_{p} p^{\lfloor \frac{n}{p}\rfloor + \lfloor \frac{n}{p^2}\rfloor +\ldots}$ ,

где произведение берется по всем простым числам.

Другие свойства

x!2 > x x > x! > = x, при x>1

Обобщения

Двойной факториал

Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1,_n_], имеющих ту же чётность что и n. Таким образом,

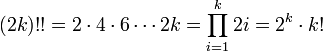
$(2k)!! = 2\cdot 4\cdot 6\cdots 2k =\prod_{i=1}^{k} 2i = 2^k\cdot k!$

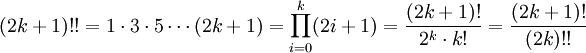
$(2k+1)!! = 1\cdot 3\cdot 5\cdots (2k+1) = \prod_{i=0}^{k} (2i+1) = \frac{(2k+1)!}{2^k\cdot k!} = \frac{(2k+1)!}{(2k)!!}$

По определению полагают 0!! = 1.

Убывающий факториал

Убывающим факториалом (или неполным факториалом) называется выражение

$(n)_k = n^{\underline{k}} = n^{[k]}= n\cdot (n-1)\cdot \ldots\cdot (n-k+1) = \frac{n!}{(n-k)!}$

Убывающий факториал дает число размещений из n по k.

Возрастающий факториал

Возрастающим факториалом называется выражение

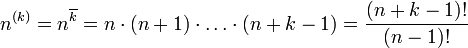
$n^{(k)} = n^{\overline{k}} = n\cdot (n+1)\cdot \ldots\cdot (n+k-1) = \frac{(n+k-1)!}{(n-1)!}$

Праймориал или примориал

Примориал (англ. Primorial) числа n обозначается _n_# и определяется как произведение простых чисел, не превышающих n. Например,

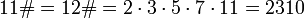
$11\# = 12\# = 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 = 2310$

Последовательность праймориалов начинается так:

2, 6, 30, 210, 2310, 30030, 510510, 9699690, … (последовательность A002110 в OEIS)

Суперфакториалы

Основная статья: Большие числа

Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению суперфакториал четырёх равен (поскольку устоявшегося обозначения нет, используется функциональное)

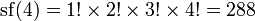
$\operatorname{sf}(4)=1! \times 2! \times 3! \times 4!=288 \,$

В общем

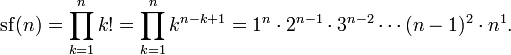
$\operatorname{sf}(n) =\prod_{k=1}^n k! =\prod_{k=1}^n k^{n-k+1} =1^n\cdot2^{n-1}\cdot3^{n-2}\cdots(n-1)^2\cdot n^1.$

Последовательность суперфакториалов начинается (с n = 0) с

1, 1, 2, 12, 288, 34560, 24883200, … (последовательность A000178 в OEIS)

Идея была обобщена в 2000 Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Super-duper-factorial), которые являются произведением первых n суперфакториалов. Первые члены (с n = 0) равны:

1, 1, 2, 24, 6912, 238878720, 5944066965504000, … (последовательность A055462 в OEIS)

Продолжая рекуррентно, можно определить факториал кратного уровня, где _m_-уровневый факториал n — произведение первых n (m − 1)-уровневых факториалов, то есть

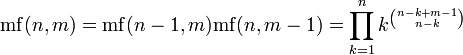
$\operatorname{mf}(n,m) = \operatorname{mf}(n-1,m)\operatorname{mf}(n,m-1) =\prod_{k=1}^n k^{n-k+m-1 \choose n-k}$

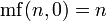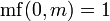где $\operatorname{mf}(n,0)=n$ для n > 0 и $\operatorname{mf}(0,m)=1$ .

Субфакториал

Субфакториал 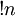$!n\!$ определяется как количество беспорядков порядка 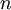$\!n$ , то есть перестановок 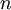$\!n$ -элементного множества без неподвижных точек.

Ссылки

Онлайн Калькулятор Факториалов

См. также

Факторион

Wikimedia Foundation.2010.