Дельта-функция Дирака | это... Что такое Дельта-функция Дирака? (original) (raw)

δ-функция (или дельта-функция, δ-функция Дирака, дираковская дельта, Единичная импульсная функция) позволяет записать пространственную плотность физической величины (масса, заряд, интенсивность источника тепла, сила и т. п.), сосредоточенной или приложенной в одной точке.

Например, плотность точечной массы 1, находящейся в точке a евклидова пространства 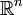$\mathbb R^n$ , записывается с помощью δ-функции в виде δ(x − a). Также применима для описания распределений заряда, массы и т. п. на поверхностях или линиях.

δ-функция есть обобщённая функция, это означает, что формально она определяется как непрерывный линейный функционал на пространстве дифференцируемых функций.

δ-функция не является функцией в классическом смысле, тем не менее нетрудно указать последовательности обычных классических функций, слабо сходящуюся к δ-функции.

Введена английским физиком Дираком.

Можно различать одномерную и многомерные дельта-функции, однако последние могут быть представлены в виде произведения одномерных в количестве, равном размерности пространства, на котором определена многомерная.

Содержание

1 Определение
2 Альтернативное определение
3 Свойства
4 δ-функция как слабый предел
5 Интегральное представление
6 Производная дельта-функции
7 Преобразование Фурье
8 Представление многомерных дельта-функций в различных системах координат
9 Физическая интерпретация
10 Литература
11 Ссылки
12 См. также

Определение

δ-функция с областью определения 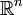$\mathbb R^n$ определяется формальным соотношением

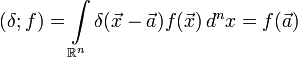
$(\delta;f)=\int\limits_{\mathbb R^n}\delta(\vec{x}-\vec{a})f(\vec{x})\,d^n x = f(\vec{a})$

для любой непрерывной функции $f(\vec{x})$ .

В частности, для одномерной дельта-функции (то есть дельта-функции с областью определения ${\mathbb R}$ )

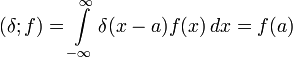$(\delta;f)=\int\limits_{-\infty}^{\infty} \delta(x-a)f(x)\, dx = f(a)$ .

Альтернативное определение

Для дельта-функции одной вещественной переменной верны следующие равенства:

$\delta(x) = 0,\qquad\forall x \not= 0$ ;
$\ \int\limits_{-\infty}^{\infty} \delta(x)\, dx = 1$ .
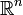
аналогичные свойства верны и для дельта-функций, определённых на $\mathbb{R}^n$

Формально эти равенства не являются определением дельта-функции, однако во многих учебниках по физике она определяется именно так, и этого достаточно для решения физических задач.

Свойства

Первообразной одномерной дельта-функции является функция Хевисайда:

$\eta(x) = \begin{cases} 0, &amp; x \leqslant 0 \\ 1, &amp; x &gt; 0 \end{cases}$

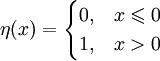
δ-функция как слабый предел

Пусть $\int\limits_{-\infty}^{+\infty} f(x)\,dx = 1.$

Тогда последовательность

~f_n(x) = n f(n x),

в некотором смысле сходится (слабо сходится) к δ-функции.

График функции 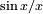$\scriptstyle{\sin x/x}$

Часто, в качестве 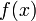~f(x) выбирают

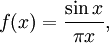
$f(x) = {\sin x \over \pi x},$

дающую последовательность

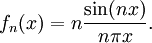
$f_n(x) = {n}{\sin (n x) \over n{\pi} x}.$

Если нужно, чтобы члены последовательности были всюду положительными функциями, можно исходить из Гауссова колокола :

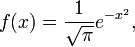
$f(x) = \frac1{\sqrt{\pi}}e^{-x^2},$

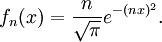
$f_n(x) = \frac{n}{\sqrt{\pi}} e^{-(n x)^2}.$

Интегральное представление

Во многих приложениях оказывается удобным интегральное представление дельта-функции:

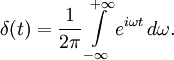
$\delta(t) = \frac{1}{2\pi} \int\limits_{-\infty}^{+\infty} e^{i\omega t}\, d\omega.$

Доказательство

Рассмотрим интеграл

$I(t) = \frac{1}{2\pi} \int\limits_{-\infty}^\infty e^{i\omega t}\, d\omega,$ (1)

который можно интерпретировать как предел

$I(t) = \lim_{N \to \infty} I_N(t),$

где

$I_N(t) = \frac{1}{2\pi} \int\limits_{-N}^N e^{i\omega t}\, d\omega = \frac{1}{\pi} N \frac{\sin{tN}}{tN}.$ (2)

График функции s i n(x) / x

Известно, что

$\int\limits_{-\infty}^ \infty \frac{\sin{t}}{t}\,dt = \pi.$ (3)

В силу (3) для любого N справедливо равенство:

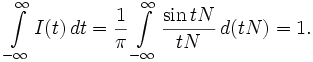$\int\limits_{-\infty}^{\infty} I(t)\, dt = \frac{1}{\pi} \int\limits_{-\infty}^{\infty} \frac{\sin{tN}}{tN}\, d(tN) = 1.$ (4)

Можно показать (см. выше), что при неограниченном росте N для функции (2) оказываются верными все свойства дельта-функции и она в некотором смысле стремится к 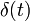$~\delta(t)$ .

Производная дельта-функции

Фундаментальное выражение, описывающее производную дельта-функции δ(x):

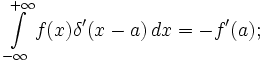
$\int\limits_{-\infty}^{+\infty}f(x)\delta^\prime(x-a)\,dx=-f^\prime(a);$

(распространение на случай подынтегральных выражений, содержащих дельта-функцию, интегрирования по частям).

Аналогично для _n_-ой производной дельта-функции:

$\int\limits_{-\infty}^{+\infty} f(x)\delta^{[n]}(x-a)\,dx = -\int\limits_{-\infty}^{+\infty}\frac{\partial f}{\partial x}\delta^{[n-1]}(x-a)\,dx.$

А проинтегрировав так по частям n раз, получим в конце концов:

$\int\limits_{-\infty}^{+\infty} f(x)\delta^{[n]}(x-a)\,dx = \left.(-1)^{n} \frac{\partial^{n} f(x)}{\partial x^{n}}\right|_{x=a}.$

Подставив же в первую формулу f(x) = x g(x) и a = 0, убедимся, что

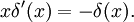
$x\delta^\prime(x)=-\delta(x).$

Для производной дельта-функции также верны следующие тождества:

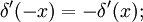
$\delta^\prime(-x)=-\delta^\prime(x);$

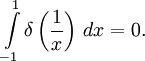
$\int\limits_{-1}^{1}\delta\left(\frac{1}{x}\right)\,dx=0.$

Преобразование Фурье

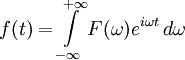В этом параграфе мы будем применять нормировку, соответствующую соглашению о единичном коэффициенте в обратном преобразовании, то есть имея в виду $f(t) =_ _\int\limits{-\infty}^{+\infty} F(\omega) e^{i \omega t}\, d\omega$ .
Формулы этого параграфа имеют соответствующие аналоги для многомерного преобразования Фурье.

К дельта-функции можно применить преобразование Фурье:

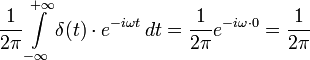$\frac{1}{2 \pi}\int\limits_{-\infty}^{+\infty}\delta(t) \cdot e^{-i \omega t}\,dt = \frac{1}{2 \pi} e^{-i \omega \cdot 0} = \frac{1}{2 \pi}$ ,

в результате получается, что спектр (фурье-образ) δ-функции является просто константой:

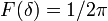$~F(\delta)=1/2\pi$ .

То есть, как и было показано выше,

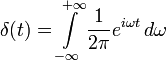$\delta(t) = \int\limits_{-\infty}^{+\infty} \frac{1}{2\pi} e^{i\omega t}\, d\omega$ .

Представление многомерных дельта-функций в различных системах координат

В _n_-мерном пространстве в декартовых координатах (ортонормированном базисе):

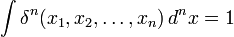$\int \delta^n (x_1, x_2, \ldots , x_n)\, d^n x = 1$ ;

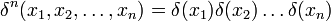$\delta^n (x_1, x_2, \ldots, x_n)=\delta(x_1)\delta(x_2)\ldots\delta(x_n)$ .

В двумерном пространстве:

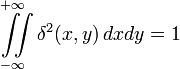$\iint\limits_{-\infty}^{+\infty}\delta^{2}(x,y)\,dxdy=1$ ;

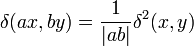$\delta(ax,by)=\frac{1}{\left|ab\right|}\delta^{2}(x,y)$ ;

δ2(x,y) = δ(x)δ(y).

В полярных координатах:

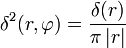$\delta^{2}(r,\varphi)=\frac{\delta(r)}{\pi\left|r\right|}$ — несмещенная относительно начала координат (с особенностью при r = 0),

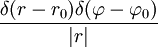$\frac{\delta(r-r_0)\delta(\varphi-\varphi_0)}{|r|}$ — с особенностью в точке общего положения 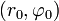$(r_0,\varphi_0)$ ; при r = 0 доопределяется нулем.

В трехмерном пространстве:

$\iiint\limits_{-\infty}^{+\infty}\delta^{3}(x,y,z)\,dxdydz=1$ ;

δ3(x,y,z) = δ(x)δ(y)δ(z);

В цилиндрической системе координат:

$\delta^{3}(r,\theta,z)=\frac{\delta(r)\delta(z)}{\pi r}$ — несмещенная относительно начала координат (с особенностью при r = 0,z = 0),

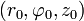$\frac{\delta(r-r_0)\delta(\varphi-\varphi_0)\delta(z-z_0)}{|r|}$ — с особенностью в точке общего положения $(r_0,\varphi_0,z_0)$ ; при r = 0 доопределяется нулем.

В сферической системе координат:

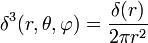$\delta^{3}(r,\theta,\varphi)=\frac{\delta(r)}{2\pi r^2}$ — несмещённая относительно начала координат (с особенностью при r = 0).

Физическая интерпретация

Вблизи заряжённой точки поле бесконечно, ряды Тейлора для поля не сходятся, поэтому вводят специальные функции. Одной из таких функций является дельта-функция. Вопрос о поле точечной заряженной частицы сравнительно сложен, поэтому рассмотрим сначала более простой пример.

Мгновенное ускорение

Пусть частица, движущаяся вдоль прямой, при ударе пренебрежимо малой длительности скачком приобретают какую-то скорость. Зададимся вопросом, как рассчитать ускорение, приобретенное телом? Построим график зависимости изменения скорости от времени. График будет иметь следующий вид:

Данный график почти всюду является графиком функции Хевисайда. Производная функции Хевисайда является единичной дельта-функцией, график которой условно можно изобразить как

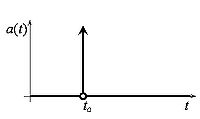
Данный график отображает бесконечное ускорение при мгновенном наборе скорости. В общем случае ускорение при ударе можно записать как

$a(t)=\nu\delta(t-t_a).\$

Масса материальной точки

Если нужно найти суммарную массу (или заряд) некоторого непрерывного распределения плотности (или плотности заряда) 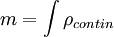$m = \int \rho_{contin}$ , содержащего кроме того точечные массы (заряды), то удобно вместо формулы, учитывающей отдельно дискретные массы и непрерывную конечную плотность:

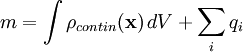
$m = \int \rho_{contin}(\mathbf{x})\, dV + \sum_i q_i$

записывать просто:

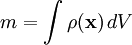
$m = \int \rho(\mathbf{x})\, dV$

имея в виду, что 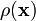$\rho(\mathbf{x})$ имеет как непрерывную, так и дельтообразные (по одной для каждой точечной массы) составляющие:

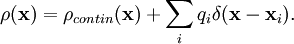
$\rho (\mathbf{x}) = \rho_{contin}(\mathbf{x}) + \sum_i q_i \delta(\mathbf{x}-\mathbf{x}_i).$

Другие примеры

Дельта-функция применяется в математической физике при решении задач, в которые входят сосредоточенные величины. В квазиклассическом пределе ( 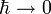$\hbar \rightarrow 0$ ) квантовой механики волновые функции локализуются в волновые пакеты с дельтаобразными (то есть имеющими в пределе форму дельта-функции) огибающими, и области их локализации движутся по классическим траекториям согласно уравнениям Ньютона.
Преобразование Фурье синуса является дельта-функцией. Это позволяет более удобно и математически строго формулировать различные задачи, связанные с преобразованием Фурье, которые очень многочисленны: волновая оптика, акустика, теория колебаний. В квантовой механике преобразования Фурье волновых функций играют первостепенную принципиальную и техническую роль, именно для неё Дирак впервые ввёл дельта-функцию.
Дельта-функции играют роль собственных функций оператора с непрерывным спектром в представленииях, где этот оператор диагонален. Таким образом, они играют роль базиса в диагональном представлении оператора.
Важным применением дельта-функции является их участие в аппарате функций Грина линейных операторов. Для линейного оператора L, действующего на обобщённые функции над многообразием M, уравнение, определяющее функцию Грина g с источником в точке _x_0, имеет вид

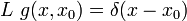$L\ g(x,x_0)= \delta (x-x_0)\$ .

Особенно часто встречается применение этого аппарата к оператору Лапласа (электростатика, теплопроводность, диффузия, механическая теория упругости) и подобным ему операторам, таким как оператор Даламбера (акустика, электродинамика, квантовая теория поля, где функция Грина часто носит специальное название пропагатора).

Для лапласиана в $\Bbb{R}^3$ функцией Грина является функция 1 / r, так что

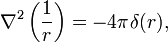
$\nabla^2\left(\frac{1}{r}\right)=-4\pi\delta(r),$

где r — расстояние до начала координат. Этот факт используется для доказательства того, что выражение для скалярного потенциала:

$\Phi(\mathbf{x})= - \int{\varrho(\mathbf{x}^\prime)\over\left|\mathbf{x}-\mathbf{x}^\prime\right|}\, d^3x^\prime$

удовлетворяет уравнению Пуассона:

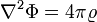
$\nabla^2\Phi=4\pi\varrho$

Литература

Дирак П. А. М. Основы квантовой механики, пер. с англ., — М., 1932 (есть много переизданий).

Ссылки

Кудрявцев Л. Д. Краткий курс математического анализа, том 2, — ISBN 5-9221-0185-4
Weisstein, Eric W. Delta Function на сайте Wolfram MathWorld.(англ.)

См. также

Wikimedia Foundation.2010.