Инварианты | это... Что такое Инварианты? (original) (raw)

Инвариа́нт — термин, используемый в математике и физике, а также в программировании, обозначает нечто неизменяемое. Кроме того, инварианты используются в олимпиадных задачах по математике для школьников. Абстрактная структурная единица языка - фонема, морфема, лексема и т.п. - в отвлечении от её конкретных реализаций (в лингвистике).

Содержание

Инварианты в математике

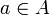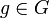Пусть A — множество и G — множество отображений из A в A. Отображение f из A во множество B называется инвариантом для G, если для любых a\in A и g\in G выполняется тождество f(a) = f(g(a)).

Примеры инвариантов:

Концепция инварианта является одной из важнейших в математике, поскольку изучение инварианта непосредственно связано с задачами классификации объектов того или иного типа. По существу, целью всякой математической классификации является построение некоторой полной системы инвариантов (по возможности, наиболее простой), то есть такой системы, которая разделяет любые два неэквивалентных объекта из рассматриваемой совокупности. (В.Л.Попов, Инвариант, Математическая энциклопедия, т.2, М.: Советская энциклопедия, 1979, С. 526.)

Инварианты в олимпиадной математике

Понятие инварианта можно проиллюстрировать на следующей задаче:

Ребёнок овладел всего лишь двумя звуками: "У" и "А", причем два слова в лексиконе этого ребёнка означают одно и то же, если одно получается из другого при помощи следующих преобразований: исключения идущих подряд звуков "УА" или "ААУУ" и добавления в любое место сочетания "АУУА". Докажите, что слова "ААУАААУУА" и "ААУУААА" означают одно и то же.

Нетрудно проверить, что второе слово получается из первого в результате последовательного применения трёх преобразований, указанных выше (назовём их смыслосохраняющими преобразованиями) — надо только найти эту цепочку смыслосохраняющих преобразований. Однако, на вопрос, означают ли слова "АУУ" и "УАА" одно и то же, ответить гораздо сложнее. Перебор последовательностей смыслосохраняющих преобразований не позволит получить второе слово из первого, так как данные слова имеют разный смысл. Для доказательства этого нужен принципиально другой подход, именуемый поиском инварианта.[1][2]

Инварианты в физике

В физических процессах всегда существуют величины, которые не изменяются с течением времени, они и называются инвариантами. Примеры: энергия, компоненты импульса и момента импульса в замкнутых системах.

Также инвариантами называются величины, независимые от условий наблюдения, в особенности - от системы отсчета - например интервал в теории относительности инвариантен в этом смысле. Промежуток времени между двумя событиями, а также расстояние между ними (местами событий) для наблюдателей, движущихся в различных направлениях с разными скоростями, будут разными, однако интервал между этими событиями для всех наблюдателей будет один. К этой же категории относится, например скорость света в вакууме. Такие величины, в зависимости от класса систем отсчета, при переходе между которыми сохраняется инвариантность данной величины, называют лоренц-инвариантными (инвариантами группы Лоренца) или инвариантами группы общекоординатных преобразований (рассматриваемыми в общей теории относительности); для ньютоновской физики может иметь смысл также рассматривать инвариантность относительно преобразований Галилея (инвариантными относительно таких преобразований являются компоненты ускорения и силы).

Понятие инвариантности (инвариантов) в физике лежит в русле принятого в математике понятия "инвариант преобразований (группы преобразований)" (той или иной конкретной группы преобразований - сдвигов времени, преобразований Лоренца итп).

Инварианты в программировании

Инвариантом называется логическое выражение, истинное после каждого прохода тела цикла (после выполнения фиксированного оператора) и перед началом выполнения цикла, зависящее от переменных, изменяющихся в теле цикла. Инварианты используются в теории верификации программ для доказательства правильности выполнения цикла. Порядок доказательства работоспособности цикла с помощью инварианта сводится к следующему:

  1. Доказывается, что выражение инварианта истинно перед началом цикла.
  2. Доказывается, что выражение инварианта сохраняет свою истинность после выполнения тела цикла; таким образом, по индукции, доказывается, что по завершении цикла инвариант будет выполняться.
  3. Доказывается, что при истинности инварианта после завершения цикла переменные примут именно те значения, которые требуется получить (это элементарно определяется из выражения инварианта и известных конечных значениях переменных, на которых основывается условие завершения цикла).
  4. Доказывается (возможно — без применения инварианта), что цикл завершится, то есть условие завершения рано или поздно будет выполнено.
  5. Истинность утверждений, доказанных на предыдущих этапах, однозначно свидетельствует о том, что цикл выполнится за конечное время и даст желаемый результат.

Также инварианты используют при проектировании и оптимизации циклических алгоритмов. Например, чтобы убедиться, что оптимизированный цикл остался корректным, достаточно доказать, что инвариант цикла не нарушен и условие завершения цикла достижимо.

Понятие инварианта также используется в объектно-ориентированном программировании для обозначения непротиворечивого состояния объекта. Подразумевается, что вызов любого метода оставляет объект в состоянии инварианта.

Инвариант в фольклористике

Инвариантом называется неизменяемая часть сюжета фольклорного произведения, которая характерна для всего сюжетного типа. Инварианту противостоит вариант.

Сюжеты, мотивы
По Ж.Польти Мольба • Спасение • Месть, преследующая преступление (глаз за глаз) • Месть, близкому за близкого • Затравленный • Внезапное несчастье • Жертва кого-нибудь • Бунт • Отважная попытка • Похищение • Загадка • Достижение • Ненависть между близкими • Соперничество между близкими • Адъюлтер, сопровождающийся убийством • Безумие • Фатальная неосторожность • Невольное кровосмешение • Невольное убийство близкого • Самопожертвование во имя идеала • Самопожертвование ради близких • Жертва безмерной радости • Жертва близким во имя долга • Соперничество неравных • Адъюлтер • Преступление любви • Бесчестие любимого существа • Любовь, встречающая препятствия (любовь с препятствиями) • Любовь к врагу • Честолюбие • Борьба против бога • Неосновательная ревность • Судебная ошибка • Угрызения совести • Вновь найденный • Потеря близких
Другие Сбивание лишних солнц с неба
Базовыепонятия Сюжет • Мотив (литература) • Мотив (искусство) • Масштабно-тематические структуры • Фабльо • Указатель сюжетов фольклорной сказки • Сказочный сюжет • Тип сказки • Жанровая модель • Сюжетный каркас • Тематический блок • Стилистическое клише • Элементарный сюжет • Бродячий сюжет • Вечные образы • Классификация сюжетов • Образ • Символ • Знак • Концепт • Инвариант • Орнамент • Структура • Каркас • Шаблон • Модель • Систематика
Жанры Литературные жанры • Музыкальные жанры • Жанры киноискусства • Риторические жанры

См. также

Ссылки

Построение цикла с помощью инварианта

Литература

Визгин В. П. Развитие взаимосвязи принципов инвариантности с законами сохранения в классической физике. М.: Наука, 1972. 240 с.

Примечания

  1. ↑ Ионин Ю., Курляндчик Л.Поиск инварианта// Журнал "Квант", 1976 г., №2.
  2. ↑ А. Толпыго Инварианты//Журнал "Квант", 1976 г., №12.

Wikimedia Foundation.2010.