Поиск в глубину | это... Что такое Поиск в глубину? (original) (raw)
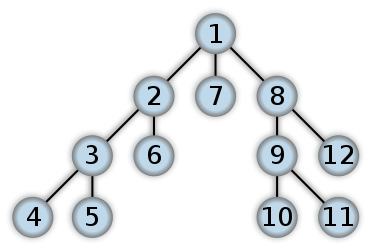
Порядок обхода дерева в глубину
Поиск в глубину (англ. Depth-first search, DFS) — один из методов обхода графа. Алгоритм поиска описывается следующим образом: для каждой непройденной вершины необходимо найти все не пройденные смежные вершины и повторить поиск для них. Используется в качестве подпрограммы в алгоритмах поиска одно- и двусвязных компонент, топологической сортировки.
Содержание
Алгоритм поиска в глубину
Пусть задан граф  , где
, где  — множество вершин графа,
— множество вершин графа,  — множество ребер графа. Предположим, что в начальный момент времени все вершины графа окрашены в белый цвет. Выполним следующие действия:
— множество ребер графа. Предположим, что в начальный момент времени все вершины графа окрашены в белый цвет. Выполним следующие действия:
- Из множества всех белых вершин выберем любую вершину, обозначим её
 .
. - Выполняем для неё процедуру
DFS(). - Повторяем шаги 1-3 до тех пор, пока множество белых вершин не пусто.
Процедура DFS (параметр — вершина  )
)
- Перекрашиваем вершину
 в черный цвет.
в черный цвет. - Для всякой вершины
 , смежной с вершиной u и окрашенной в белый цвет, выполняем процедуру
, смежной с вершиной u и окрашенной в белый цвет, выполняем процедуру DFS(w).
Недостатки
 |
В этом разделе не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена.Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники.Эта отметка установлена 21 октября 2012. |
|---|
- Во-первых, отыскивается не самый короткий путь;
- Во-вторых, если в дереве есть бесконечные ветви и если такая бесконечная ветвь встретится, поиск никогда не закончится, даже если есть конечный путь в целевую вершину.
Поиск в глубину наиболее адекватен рекурсивному стилю программирования, принятому в Прологе. Причина этого состоит в том, что, обрабатывая цели, пролог-система сама просматривает альтернативы именно в глубину.
Примеры реализации
Java
public static void dfs(Node node, Node goal) // Node - вершина графа
{
if (node.equals(goal))
{
System.out.println(node));
}
else
{
for (int i = 0; i < node.getNode().size(); i++) // Вызываем этот же метод для каждой смежной вершины
{
if (stack.add(node.getNode().get(i))) // Проверяем, вызывали ли мы этот метод для вершины node.getNode().get(i)
{
dfs(node.getNode().get(i), goal);
}
}
}
}
С++
vector < vector > graph;
vector used;
void dfs(int node_index) { used[node_index] = true; for (vector::iterator i = graph[node_index].begin(); i != graph[node_index].end(); ++i) { if ( !used[*i] ) dfs(*i); } }
Pascal
const MAX_N = 10; var graph: array [1..MAX_N, 1..MAX_N] of boolean; // массив для определения графа visited: array [1..MAX_N] of boolean;
procedure dfs(v: integer); var i: integer; begin visited[v] := true;
for i := 1 to MAX_N do if graph[v, i] and not visited[i] then dfs(i); end;
| Алгоритмы поиска на графах |
|---|
| A* B* Алгоритм Беллмана — Форда Двунаправленный поиск Алгоритм Дейкстры Алгоритм Джонсона Поиск в ширину Поиск в глубину Поиск с ограничением глубины Поиск по первому наилучшему совпадению Алгоритм Флойда — Уоршелла |
Литература
- Ананий В. Левитин Глава 5. Метод уменьшения размера задачи: Поиск в глубину // Алгоритмы: введение в разработку и анализ = Introduction to The Design and Analysis of Aigorithms. — М.: «Вильямс», 2006. — С. 212-215. — ISBN 0-201-74395-7
- Кормен Т., Лейзерсон Ч., Ривест Р. Глава 22. Элементарные алгоритмы для работы с графами // Алгоритмы: построение и анализ(второе издание). — М.: «Вильямс», 2005. — С. 622-632.