Spintronics (original) (raw)
From Wikipedia, the free encyclopedia
Solid-state electronics based on electron spin
Spintronics (a portmanteau meaning spin transport electronics[1][2][3]), also known as spin electronics, is the study of the intrinsic spin of the electron and its associated magnetic moment, in addition to its fundamental electronic charge, in solid-state devices.[4] The field of spintronics concerns spin-charge coupling in metallic systems; the analogous effects in insulators fall into the field of multiferroics.
Spintronics fundamentally differs from traditional electronics in that, in addition to charge state, electron spins are used as a further degree of freedom, with implications in the efficiency of data storage and transfer. Spintronic systems are most often realised in dilute magnetic semiconductors (DMS) and Heusler alloys and are of particular interest in the field of quantum computing and neuromorphic computing.
Spintronics emerged from discoveries in the 1980s concerning spin-dependent electron transport phenomena in solid-state devices. This includes the observation of spin-polarized electron injection from a ferromagnetic metal to a normal metal by Johnson and Silsbee (1985)[5] and the discovery of giant magnetoresistance independently by Albert Fert et al.[6] and Peter Grünberg et al. (1988).[7] The origin of spintronics can be traced to the ferromagnet/superconductor tunneling experiments pioneered by Meservey and Tedrow and initial experiments on magnetic tunnel junctions by Julliere in the 1970s.[8] The use of semiconductors for spintronics began with the theoretical proposal of a spin field-effect-transistor by Datta and Das in 1990[9] and of the electric dipole spin resonance by Rashba in 1960.[10]
The spin of the electron is an intrinsic angular momentum that is separate from the angular momentum due to its orbital motion. The magnitude of the projection of the electron's spin along an arbitrary axis is 1 2 ℏ {\displaystyle {\tfrac {1}{2}}\hbar } 
μ = 3 2 q m e ℏ {\displaystyle \mu ={\tfrac {\sqrt {3}}{2}}{\frac {q}{m_{e}}}\hbar } 
In a solid, the spins of many electrons can act together to affect the magnetic and electronic properties of a material, for example endowing it with a permanent magnetic moment as in a ferromagnet.
In many materials, electron spins are equally present in both the up and the down state, and no transport properties are dependent on spin. A spintronic device requires generation or manipulation of a spin-polarized population of electrons, resulting in an excess of spin up or spin down electrons. The polarization of any spin dependent property X can be written as
P X = X ↑ − X ↓ X ↑ + X ↓ {\displaystyle P_{X}={\frac {X_{\uparrow }-X_{\downarrow }}{X_{\uparrow }+X_{\downarrow }}}} 
A net spin polarization can be achieved either through creating an equilibrium energy split between spin up and spin down. Methods include putting a material in a large magnetic field (Zeeman effect), the exchange energy present in a ferromagnet or forcing the system out of equilibrium. The period of time that such a non-equilibrium population can be maintained is known as the spin lifetime, τ {\displaystyle \tau } 
In a diffusive conductor, a spin diffusion length λ {\displaystyle \lambda } 
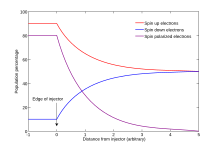
A plot showing a spin up, spin down, and the resulting spin polarized population of electrons. Inside a spin injector, the polarization is constant, while outside the injector, the polarization decays exponentially to zero as the spin up and down populations go to equilibrium.
The mechanisms of decay for a spin polarized population can be broadly classified as spin-flip scattering and spin dephasing. Spin-flip scattering is a process inside a solid that does not conserve spin, and can therefore switch an incoming spin up state into an outgoing spin down state. Spin dephasing is the process wherein a population of electrons with a common spin state becomes less polarized over time due to different rates of electron spin precession. In confined structures, spin dephasing can be suppressed, leading to spin lifetimes of milliseconds in semiconductor quantum dots at low temperatures.
Superconductors can enhance central effects in spintronics such as magnetoresistance effects, spin lifetimes and dissipationless spin-currents.[11][12]
The simplest method of generating a spin-polarised current in a metal is to pass the current through a ferromagnetic material. The most common applications of this effect involve giant magnetoresistance (GMR) devices. A typical GMR device consists of at least two layers of ferromagnetic materials separated by a spacer layer. When the two magnetization vectors of the ferromagnetic layers are aligned, the electrical resistance will be lower (so a higher current flows at constant voltage) than if the ferromagnetic layers are anti-aligned. This constitutes a magnetic field sensor.
Two variants of GMR have been applied in devices: (1) current-in-plane (CIP), where the electric current flows parallel to the layers and (2) current-perpendicular-to-plane (CPP), where the electric current flows in a direction perpendicular to the layers.
Other metal-based spintronics devices:
- Tunnel magnetoresistance (TMR), where CPP transport is achieved by using quantum-mechanical tunneling of electrons through a thin insulator separating ferromagnetic layers.
- Spin-transfer torque, where a current of spin-polarized electrons is used to control the magnetization direction of ferromagnetic electrodes in the device.
- Spin-wave logic devices carry information in the phase. Interference and spin-wave scattering can perform logic operations.
Spintronic-logic devices
[edit]
Non-volatile spin-logic devices to enable scaling are being extensively studied.[13] Spin-transfer, torque-based logic devices that use spins and magnets for information processing have been proposed.[14][15] These devices are part of the ITRS exploratory road map. Logic-in memory applications are already in the development stage.[16][17] A 2017 review article can be found in Materials Today.[4]
A generalized circuit theory for spintronic integrated circuits has been proposed [18] so that the physics of spin transport can be utilized by SPICE developers and subsequently by circuit and system designers for the exploration of spintronics for “beyond CMOS computing.”
Read heads of magnetic hard drives are based on the GMR or TMR effect.
Motorola developed a first-generation 256 kb magnetoresistive random-access memory (MRAM) based on a single magnetic tunnel junction and a single transistor that has a read/write cycle of under 50 nanoseconds.[19] Everspin has since developed a 4 Mb version.[20] Two second-generation MRAM techniques are in development: thermal-assisted switching (TAS)[21] and spin-transfer torque (STT).[22]
Another design, racetrack memory, a novel memory architecture proposed by Dr. Stuart S. P. Parkin, encodes information in the direction of magnetization between domain walls of a ferromagnetic wire.
In 2012, persistent spin helices of synchronized electrons were made to persist for more than a nanosecond, a 30-fold increase over earlier efforts, and longer than the duration of a modern processor clock cycle.[23]
Semiconductor-based spintronic devices
[edit]
Doped semiconductor materials display dilute ferromagnetism. In recent years, dilute magnetic oxides (DMOs) including ZnO based DMOs and TiO2-based DMOs have been the subject of numerous experimental and computational investigations.[24][25] Non-oxide ferromagnetic semiconductor sources (like manganese-doped gallium arsenide (Ga,Mn)As),[26] increase the interface resistance with a tunnel barrier,[27] or using hot-electron injection.[28]
Spin detection in semiconductors has been addressed with multiple techniques:
- Faraday/Kerr rotation of transmitted/reflected photons[29]
- Circular polarization analysis of electroluminescence[30]
- Nonlocal spin valve (adapted from Johnson and Silsbee's work with metals)[31]
- Ballistic spin filtering[32]
The latter technique was used to overcome the lack of spin-orbit interaction and materials issues to achieve spin transport in silicon.[33]
Because external magnetic fields (and stray fields from magnetic contacts) can cause large Hall effects and magnetoresistance in semiconductors (which mimic spin-valve effects), the only conclusive evidence of spin transport in semiconductors is demonstration of spin precession and dephasing in a magnetic field non-collinear to the injected spin orientation, called the Hanle effect.
Applications using spin-polarized electrical injection have shown threshold current reduction and controllable circularly polarized coherent light output.[34] Examples include semiconductor lasers. Future applications may include a spin-based transistor having advantages over MOSFET devices such as steeper sub-threshold slope.
Magnetic-tunnel transistor: The magnetic-tunnel transistor with a single base layer[35] has the following terminals:
- Emitter (FM1): Injects spin-polarized hot electrons into the base.
- Base (FM2): Spin-dependent scattering takes place in the base. It also serves as a spin filter.
- Collector (GaAs): A Schottky barrier is formed at the interface. It only collects electrons that have enough energy to overcome the Schottky barrier, and when states are available in the semiconductor.
The magnetocurrent (MC) is given as:
M C = I c , p − I c , a p I c , a p {\displaystyle MC={\frac {I_{c,p}-I_{c,ap}}{I_{c,ap}}}}
And the transfer ratio (TR) is
T R = I C I E {\displaystyle TR={\frac {I_{C}}{I_{E}}}}
MTT promises a highly spin-polarized electron source at room temperature.
Antiferromagnetic storage media have been studied as an alternative to ferromagnetism,[36] especially since with antiferromagnetic material the bits can be stored as well as with ferromagnetic material. Instead of the usual definition 0 ↔ 'magnetisation upwards', 1 ↔ 'magnetisation downwards', the states can be, e.g., 0 ↔ 'vertically-alternating spin configuration' and 1 ↔ 'horizontally-alternating spin configuration'.[37]).
The main advantages of antiferromagnetic material are:
- insensitivity to data-damaging perturbations by stray fields due to zero net external magnetization;[38]
- no effect on near particles, implying that antiferromagnetic device elements would not magnetically disturb its neighboring elements;[38]
- far shorter switching times (antiferromagnetic resonance frequency is in the THz range compared to GHz ferromagnetic resonance frequency);[39]
- broad range of commonly available antiferromagnetic materials including insulators, semiconductors, semimetals, metals, and superconductors.[39]
Research is being done into how to read and write information to antiferromagnetic spintronics as their net zero magnetization makes this difficult compared to conventional ferromagnetic spintronics. In modern MRAM, detection and manipulation of ferromagnetic order by magnetic fields has largely been abandoned in favor of more efficient and scalable reading and writing by electrical current. Methods of reading and writing information by current rather than fields are also being investigated in antiferromagnets as fields are ineffective anyway. Writing methods currently being investigated in antiferromagnets are through spin-transfer torque and spin-orbit torque from the spin Hall effect and the Rashba effect. Reading information in antiferromagnets via magnetoresistance effects such as tunnel magnetoresistance is also being explored.[40]
- Stuart S. P. Parkin
- Electric dipole spin resonance
- Josephson effect
- Magnetoresistive random-access memory (MRAM)
- Magnonics
- Potential applications of graphene#Spintronics
- Rashba effect
- Spin pumping
- Spin-transfer torque
- Spinhenge@Home
- Spinmechatronics
- Spinplasmonics
- Unconventional computing
- Valleytronics
- List of emerging technologies
- Multiferroics
- ^ Wolf, S. A.; Chtchelkanova, A. Y.; Treger, D. M. (2006). "Spintronics—A retrospective and perspective". IBM Journal of Research and Development. 50: 101–110. doi:10.1147/rd.501.0101.
- ^ "Physics Profile: "Stu Wolf: True D! Hollywood Story"". Archived from the original on 18 April 2011. Retrieved 11 July 2008.
- ^ Spintronics: A Spin-Based Electronics Vision for the Future. Sciencemag.org (16 November 2001). Retrieved on 21 October 2013.
- ^ a b Bhatti, S.; et al. (2017). "Spintronics based random access memory: a review". Materials Today. 20 (9): 530–548. doi:10.1016/j.mattod.2017.07.007. hdl:10356/146755.
- ^ Johnson, M.; Silsbee, R. H. (1985). "Interfacial charge-spin coupling: Injection and detection of spin magnetization in metals". Physical Review Letters. 55 (17): 1790–1793. Bibcode:1985PhRvL..55.1790J. doi:10.1103/PhysRevLett.55.1790. PMID 10031924.
- ^ Baibich, M. N.; Broto, J. M.; Fert, A.; Nguyen Van Dau, F. N.; Petroff, F.; Etienne, P.; Creuzet, G.; Friederich, A.; Chazelas, J. (1988). "Giant Magnetoresistance of (001)Fe/(001)Cr Magnetic Superlattices" (PDF). Physical Review Letters. 61 (21): 2472–2475. Bibcode:1988PhRvL..61.2472B. doi:10.1103/PhysRevLett.61.2472. PMID 10039127.
- ^ Binasch, G.; Grünberg, P.; Saurenbach, F.; Zinn, W. (1989). "Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange". Physical Review B. 39 (7): 4828–4830. Bibcode:1989PhRvB..39.4828B. doi:10.1103/PhysRevB.39.4828. PMID 9948867.
- ^ Julliere, M. (1975). "Tunneling between ferromagnetic films". Physics Letters A. 54 (3): 225–226. Bibcode:1975PhLA...54..225J. doi:10.1016/0375-9601(75)90174-7.
- ^ Datta, S. & Das, B. (1990). "Electronic analog of the electrooptic modulator". Applied Physics Letters. 56 (7): 665–667. Bibcode:1990ApPhL..56..665D. doi:10.1063/1.102730.
- ^ E. I. Rashba, Cyclotron and combined resonances in a perpendicular field, Sov. Phys. Solid State 2, 1109 -1122 (1960)
- ^ Linder, Jacob; Robinson, Jason W. A. (2 April 2015). "Superconducting spintronics". Nature Physics. 11 (4): 307–315. arXiv:1510.00713. Bibcode:2015NatPh..11..307L. doi:10.1038/nphys3242. ISSN 1745-2473. S2CID 31028550.
- ^ Eschrig, Matthias (2011). "Spin-polarized supercurrents for spintronics". Physics Today. 64 (1): 43–49. Bibcode:2011PhT....64a..43E. doi:10.1063/1.3541944.
- ^ International Technology Roadmap for Semiconductors
- ^ Behin-Aein, B.; Datta, D.; Salahuddin, S.; Datta, S. (2010). "Proposal for an all-spin logic device with built-in memory". Nature Nanotechnology. 5 (4): 266–270. Bibcode:2010NatNa...5..266B. doi:10.1038/nnano.2010.31. PMID 20190748.
- ^ Manipatruni, Sasikanth; Nikonov, Dmitri E. and Young, Ian A. (2011) [1112.2746] Circuit Theory for SPICE of Spintronic Integrated Circuits. Arxiv.org. Retrieved on 21 October 2013.
- ^ Crocus Partners With Starchip To Develop System-On-Chip Solutions Based on Magnetic-Logic-Unit (MLU) Technology. crocus-technology.com. 8 December 2011
- ^ Groundbreaking New Technology for Improving the Reliability of Spintronics Logic Integrated Circuits. Nec.com. 11 June 2012.
- ^ S. Manipatruni, D. E. Nikonov and I. A. Young, "Modeling and Design of Spintronic Integrated Circuits," in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 59, no. 12, pp. 2801-2814, Dec. 2012, doi: 10.1109/TCSI.2012.2206465. https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=6359950&isnumber=6359940
- ^ Spintronics. Sigma-Aldrich. Retrieved on 21 October 2013.
- ^ Everspin Archived 30 June 2012 at the Wayback Machine. Everspin. Retrieved on 21 October 2013.
- ^ Hoberman, Barry. The Emergence of Practical MRAM Archived 21 October 2013 at the Wayback Machine. crocustechnology.com
- ^ LaPedus, Mark (18 June 2009) Tower invests in Crocus, tips MRAM foundry deal. eetimes.com
- ^ Walser, M.; Reichl, C.; Wegscheider, W. & Salis, G. (2012). "Direct mapping of the formation of a persistent spin helix". Nature Physics. 8 (10): 757. arXiv:1209.4857. Bibcode:2012NatPh...8..757W. doi:10.1038/nphys2383. S2CID 119209785.
- ^ Assadi, M.H.N; Hanaor, D.A.H (2013). "Theoretical study on copper's energetics and magnetism in TiO2 polymorphs". Journal of Applied Physics. 113 (23): 233913–233913–5. arXiv:1304.1854. Bibcode:2013JAP...113w3913A. doi:10.1063/1.4811539. S2CID 94599250.
- ^ Ogale, S.B (2010). "Dilute doping, defects, and ferromagnetism in metal oxide systems". Advanced Materials. 22 (29): 3125–3155. Bibcode:2010AdM....22.3125O. doi:10.1002/adma.200903891. PMID 20535732. S2CID 25307693.
- ^ Jonker, B.; Park, Y.; Bennett, B.; Cheong, H.; Kioseoglou, G.; Petrou, A. (2000). "Robust electrical spin injection into a semiconductor heterostructure". Physical Review B. 62 (12): 8180. Bibcode:2000PhRvB..62.8180J. doi:10.1103/PhysRevB.62.8180.
- ^ Hanbicki, A. T.; Jonker, B. T.; Itskos, G.; Kioseoglou, G.; Petrou, A. (2002). "Efficient electrical spin injection from a magnetic metal/tunnel barrier contact into a semiconductor". Applied Physics Letters. 80 (7): 1240. arXiv:cond-mat/0110059. Bibcode:2002ApPhL..80.1240H. doi:10.1063/1.1449530. S2CID 119098659.
- ^ Jiang, X.; Wang, R.; Van Dijken, S.; Shelby, R.; MacFarlane, R.; Solomon, G.; Harris, J.; Parkin, S. (2003). "Optical Detection of Hot-Electron Spin Injection into GaAs from a Magnetic Tunnel Transistor Source". Physical Review Letters. 90 (25): 256603. Bibcode:2003PhRvL..90y6603J. doi:10.1103/PhysRevLett.90.256603. PMID 12857153.
- ^ Kikkawa, J.; Awschalom, D. (1998). "Resonant Spin Amplification in n-Type GaAs". Physical Review Letters. 80 (19): 4313. Bibcode:1998PhRvL..80.4313K. doi:10.1103/PhysRevLett.80.4313.
- ^ Jonker, Berend T. Polarized optical emission due to decay or recombination of spin-polarized injected carriers – US Patent 5874749 Archived 12 December 2009 at the Wayback Machine. Issued on 23 February 1999.
- ^ Lou, X.; Adelmann, C.; Crooker, S. A.; Garlid, E. S.; Zhang, J.; Reddy, K. S. M.; Flexner, S. D.; Palmstrøm, C. J.; Crowell, P. A. (2007). "Electrical detection of spin transport in lateral ferromagnet–semiconductor devices". Nature Physics. 3 (3): 197. arXiv:cond-mat/0701021. Bibcode:2007NatPh...3..197L. doi:10.1038/nphys543. S2CID 51390849.
- ^ Appelbaum, I.; Huang, B.; Monsma, D. J. (2007). "Electronic measurement and control of spin transport in silicon". Nature. 447 (7142): 295–298. arXiv:cond-mat/0703025. Bibcode:2007Natur.447..295A. doi:10.1038/nature05803. PMID 17507978. S2CID 4340632.
- ^ Žutić, I.; Fabian, J. (2007). "Spintronics: Silicon twists". Nature. 447 (7142): 268–269. Bibcode:2007Natur.447..268Z. doi:10.1038/447269a. PMID 17507969. S2CID 32830840.
- ^ Holub, M.; Shin, J.; Saha, D.; Bhattacharya, P. (2007). "Electrical Spin Injection and Threshold Reduction in a Semiconductor Laser". Physical Review Letters. 98 (14): 146603. Bibcode:2007PhRvL..98n6603H. doi:10.1103/PhysRevLett.98.146603. PMID 17501298.
- ^ Van Dijken, S.; Jiang, X.; Parkin, S. S. P. (2002). "Room temperature operation of a high output current magnetic tunnel transistor". Applied Physics Letters. 80 (18): 3364. Bibcode:2002ApPhL..80.3364V. doi:10.1063/1.1474610.
- ^ Jungwirth, T. (28 April 2014). "Relativistic Approaches to Spintronics with Antiferromagnets" (PDF) (announcement of a physics colloquium at a Bavarian university). Archived from the original (PDF) on 29 April 2014. Retrieved 29 April 2014.
- ^ This corresponds mathematically to the transition from the rotation group SO(3) to its relativistic covering, the "double group" SU(2)
- ^ a b Jungwirth, T.; Marti, X.; Wadley, P.; Wunderlich, J. (2016). "Antiferromagnetic spintronics". Nature Nanotechnology. 11 (3). Springer Nature: 231–241. arXiv:1509.05296. Bibcode:2016NatNa..11..231J. doi:10.1038/nnano.2016.18. ISSN 1748-3387. PMID 26936817. S2CID 5058124.
- ^ a b Gomonay, O.; Jungwirth, T.; Sinova, J. (21 February 2017). "Concepts of antiferromagnetic spintronics". Physica Status Solidi RRL. 11 (4). Wiley: 1700022. arXiv:1701.06556. Bibcode:2017PSSRR..1100022G. doi:10.1002/pssr.201700022. ISSN 1862-6254. S2CID 73575617.
- ^ Chappert, Claude; Fert, Albert; van Dau, Frédéric Nguyen (2007). "The emergence of spin electronics in data storage". Nature Materials. 6 (11). Springer Science and Business Media LLC: 813–823. Bibcode:2007NatMa...6..813C. doi:10.1038/nmat2024. ISSN 1476-1122. PMID 17972936. S2CID 21075877.
- "Introduction to Spintronics". Marc Cahay, Supriyo Bandyopadhyay, CRC Press, ISBN 0-8493-3133-1
- J. A. Gupta; R. Knobel; N. Samarth; D. D. Awschalom (29 June 2001). "Ultrafast Manipulation of Electron Spin Coherence". Science. 292 (5526): 2458–2461. Bibcode:2001Sci...292.2458G. doi:10.1126/science.1061169. PMID 11431559. S2CID 22898874.
- Wolf, S. A.; Awschalom, DD; Buhrman, RA; Daughton, JM; von Molnár, S; Roukes, ML; Chtchelkanova, AY; Treger, DM (16 November 2001). "Spintronics: A Spin-Based Electronics Vision for the Future". Science. 294 (5546): 1488–1495. Bibcode:2001Sci...294.1488W. doi:10.1126/science.1065389. PMID 11711666. S2CID 14010432.
- Sharma, P. (28 January 2005). "How to Create a Spin Current". Science. 307 (5709): 531–533. doi:10.1126/science.1099388. PMID 15681374. S2CID 118636399.
- Tomasz Dietl; David D. Awschalom; Maria Kaminska; et al., eds. (2009). Spintronics. Academic Press. ISBN 9780080914213.
- Žutić, I.; Das Sarma, S. (2004). "Spintronics: Fundamentals and applications". Reviews of Modern Physics. 76 (2): 323–410. arXiv:cond-mat/0405528. Bibcode:2004RvMP...76..323Z. doi:10.1103/RevModPhys.76.323. S2CID 119398474.
- Parkin, Stuart; Ching-Ray, Chang; Chantrell, Roy, eds. (2011). "SPIN". World Scientific. ISSN 2010-3247.
- "Spintronics Steps Forward.", University of South Florida News
- Bader, S. D.; Parkin, S. S. P. (2010). "Spintronics". Annual Review of Condensed Matter Physics. 1: 71–88. Bibcode:2010ARCMP...1...71B. doi:10.1146/annurev-conmatphys-070909-104123.
- 23 milestones in the history of spin compiled by Nature
- Milestone 18: A Giant Leap for Electronics: Giant Magneto-resistance, compiled by Nature
- Milestone 20: Information in a Spin: Datta-Das, compiled by Nature
- Awschalom, David D.; Flatté, Michael E.; Samarth, Nitin (June 2002). "Spintronics". Scientific American. 286 (6): 66–73. Bibcode:2002SciAm.286f..66A. doi:10.1038/scientificamerican0602-66. PMID 12030093.
- Spintronics portal with news and resources
- RaceTrack:InformationWeek (April 11, 2008) Archived 14 April 2008 at the Wayback Machine
- Spintronics research targets GaAs.
- Spintronics Tutorial
- Lecture on Spin transport by S. Datta (from Datta Das transistor)—Part 1 and Part 2