Structure-Encoded Global Motions and Their Role in Mediating Protein-Substrate Interactions (original) (raw)

Abstract

Recent structure-based computational studies suggest that, in contrast to the classical description of equilibrium fluctuations as wigglings and jigglings, proteins have access to well-defined spectra of collective motions, called intrinsic dynamics, encoded by their structure under native state conditions. In particular, the global modes of motions (at the low frequency end of the spectrum) are shown by multiple studies to be highly robust to minor differences in the structure or to detailed interactions at the atomic level. These modes, encoded by the overall fold, usually define the mechanisms of interactions with substrates. They can be estimated by low-resolution models such as the elastic network models (ENMs) exclusively based on interresidue contact topology. The ability of ENMs to efficiently assess the global motions intrinsically favored by the overall fold as well as the relevance of these predictions to the dominant changes in structure experimentally observed for a given protein in the presence of different substrates suggest that the intrinsic dynamics plays a role in mediating protein-substrate interactions. These observations underscore the functional significance of structure-encoded dynamics, or the importance of the predisposition to favor functional global modes in the evolutionary selection of structures.

Main Text

Proteins perform their function via chemical and physical changes. Chemical changes include catalysis, posttranslational modification, cross-link formation, and covalent binding/unbinding of ligands. Physical changes involve domain rearrangements, allosteric changes in conformations (intramolecular), and protein-ligand interactions, multimerization, and formation of complexes and assemblies (intermolecular). The combination of chemical and physical (or mechanical) properties leads to unique mechanochemical behavior essential to biological activity (1). Some activities require high precision (e.g., positioning of catalytic residues in enzymes), whereas others rely on modular structures (or substructures) that are adaptable to different functionalities, e.g., binding different substrates by ubiquitin, or different antigens by antibodies. Conformational flexibility accompanied by sequence variations ensures in the latter case the adaptation to binding different substrates, and to mediate substrate specificity (2,3). Conformational flexibility that is highly specific in its directionality is essential for allosteric responses, too. It is, usually, via a conformational switch triggered by a first ligand binding (to an allosteric site) that another (recruitment) site reconfigures to facilitate its recognition by another ligand (4,5). How does the protein strike the right balance between rigidity and flexibility? How does it elicit the specific type of conformational switch that leads the way to its biological function? How does it ensure that those functional responses are robustly maintained?

Studies attempting to bridge between structure and function have led to the prominent view that the link between structure and function is through dynamics (6). Dynamics refers to changes in the chemical or physical state (reaction dynamics or interaction dynamics, respectively). The perspective of our study focuses on physical changes. We consider the changes in conformation because of substrate binding or allosteric interactions under physiological conditions—the conditions under which biomolecules accomplish their biological functions. We will submit the views that 1) each protein fold has a unique dynamics, called intrinsic dynamics, encoded by its structure under equilibrium conditions; 2) current structure-based computational approaches can provide a good first glimpse of proteins’ intrinsic dynamics at the microscopic scale, broadly consistent with experimental data, despite inherent limitations and simplifications in the models and methods; and 3) predicted dynamics has functional significance, and could be exploited for design, engineering, and therapy purposes (e.g., for exploring the druggability of target proteins). We conclude by inviting attention to the significance of intrinsic dynamic propensities in protein design and evolution; and we discuss recent studies suggesting that structure-encoded dynamics is evolutionary optimized and regulated by robust mechanisms.

Each protein has a unique intrinsic dynamics, which may be quantitatively explored by structure-based computational models and methods

In principle, the dynamics of each protein is governed by the forces experienced by its atoms as a result of intramolecular and intermolecular interactions; and to the extent that the force field provides an adequate description of these interaction potentials, the way the protein samples the conformational space in molecular simulations is a deterministic process (assuming Newtonian dynamics): it is fully determined by the atomic positions, or the instantaneous structure of the protein in the examined force field. Although the highly nonlinear interactions and in particular the aqueous environment introduce an apparent stochasticity, a given protein in a given environment has in principle its own dynamic character uniquely defined by the spatial distribution of its atoms.

One method that found wide applications in characterizing the unique dynamics of each protein near its native state conditions is normal mode analysis (NMA) (7). NMA applies to the close neighborhood of the native state (energy minimum). It yields the spectrum of modes intrinsically accessible under equilibrium conditions. These vary over a broad range, from global (modes that cooperatively involve significant portions of the structure, if not the entire structure, usually at the low-frequency end of the spectrum) to local (at the high-frequency end). Each structure has a unique spectrum of modes, also called collective motions. Note that in a strict sense, the normal modes hold in the infinitesimal proximity of the global energy minimum, and as such, they provide insights into the intrinsic tendency or predisposition of the protein to undergo particular changes in structure near its native state.

An important feature of collective motions extracted by NMA is the robustness of the computed global modes. It has been widely established and confirmed by many studies that global modes are insensitive to precise atomic coordinates or detailed force field parameters, but they are robustly defined by the overall fold/architecture of the biomolecular system, or by the topology of interresidue contacts. This fundamental concept, first shown in the pioneering coarse-grained NMA of Tirion (8), prompted the introduction of elastic network models (ENMs) for delineating the equilibrium dynamics of biomolecular systems, starting from the Gaussian Network Model (GNM) (9,10), followed by coarse-grained NMA with ENM variants by Hinsen, Perahia, and coworkers (11–13). A natural extension broadly used has been the anisotropic network model (ANM) (14). The main advantage of ANM analysis, like other ENM-NMA, is the ability to efficiently yield a unique solution for the collective motions of the examined structure without the need to perform any simulations or energy minimization. This is achieved by eigenvalue decomposition of a simple, closed-form expression for the Hessian—a 3N × 3N matrix composed of N × N submatrices of the following form (14):

Hij=−γijRij2[xij2xijyijxijzijxijyijyij2yijzijxijzijyijzijzij2],

for i ≠ j, where x ij,y ij,z ij are the _x_-, y_-, and z_-components of the distance vector Rij between nodes i and j, directly taken from the known (e.g., crystal) structure; the spring constant γ_ij = γ, if the distance R ij between nodes i and j is shorter than a cutoff distance r c, and zero otherwise; and H ii = Σ_j H ij, where the summation is over off diagonal elements. There have been various formalisms in the literature for choosing the spring constants, ranging from this simplest formulation to detailed approaches customized per protein (15). In particular, the use of a distance-dependent expression for γ that helps eliminate the parameter r c has been broadly adopted (11,16). Most of these approaches usually emphasize the need to use stiffer springs for covalently bonded pairs of residues. However, the results from ENMs, and in particular the predicted global modes, have been consistently shown to be robust to changes in spring function and parameters (see, for example, (17)).

As a corollary to the deterministic nature of molecular motions and interactions, molecular dynamics (MD) simulations would, in principle, provide us with an accurate description of biomolecular systems dynamics near their equilibrium (native) coordinates—if the generated trajectories are long enough to thoroughly sample the conformational space. Unfortunately, this is not the case, even with the most advanced simulation hardware and software. Remarkable successes have been made in developing MD methodologies applicable to systems of the order of 108 atoms (18,19), or conducting millisecond-range simulations (20). Yet, the former is restricted to the timescale of nanoseconds, and the latter, to small proteins only. However, MD convergence studies clearly show that it is impossible to obtain statistically significant data from full atomic MD simulations on the time evolution of many biological processes of interest (21,22). In contrast, ENM offers significant advantage for its computational efficiency and easy usage with orders of magnitude less computational expensive.

ENMs have their own limitations. They are coarse-grained—they usually describe the protein at the level of one-node-per-residue, each residue being identified by the position of its Cα-atom. They do not take account of specific interactions: all interresidue interactions are represented by a uniform harmonic potential between residue pairs connected in the network (which are within a cutoff separation). The network connectivity, or the spatial distribution of the nodes and springs, fully defines the dynamics of the structure represented as an ENM. Third, ENMs do not (usually) take account of the solvent or lipid environment. Finally, by definition, they do not incorporate nonlinear effects nor couplings between modes. The ENM formalism assumes fluctuations about a single well. As such, it may not be suitable for modeling the conformational dynamics of flexible objects such as loops that have multiple populated states.

Despite all limitations and simplifications, structure-based computations can provide a mechanistic description of the unique dynamics, often consistent with experiments

Despite all these limitations, computational models and methods are useful. The question often reduces to deciding which particular properties, or processes, are of interest, and choosing the proper model and methods depending on the specific time and length windows that are being examined. For example, if the goal is to have a detailed atomic understanding of the mechanism of extracellular (EC) gate opening by a given neurotransmitter transporter, one essentially examines by MD simulations the interactions near the binding site, or near the extracellular (EC) vestibule (Fig. 1, A_–_C) in the presence of the whole structure. Simulations up to 100s of nanoseconds are sufficient to consistently view substrate binding and EC gate closure or opening events in transporters, for example, in the presence of explicit membrane, water molecules, ions, and substrate molecules. In addition to elucidating the behavior of individual proteins, MD data permit us to make inferences on the common mechanisms of function selected by family members that share similar folds despite sequence dissimilarities, or the distinctive mechanisms for binding different ligands. The comparison of the behavior of dopamine transporter (DAT) and leucine transporter (LeuT), both sharing the LeuT fold, clearly elucidates the equivalent role of particular residues in EC (or intracellular, IC) gating (Fig. 1, A_–_C).

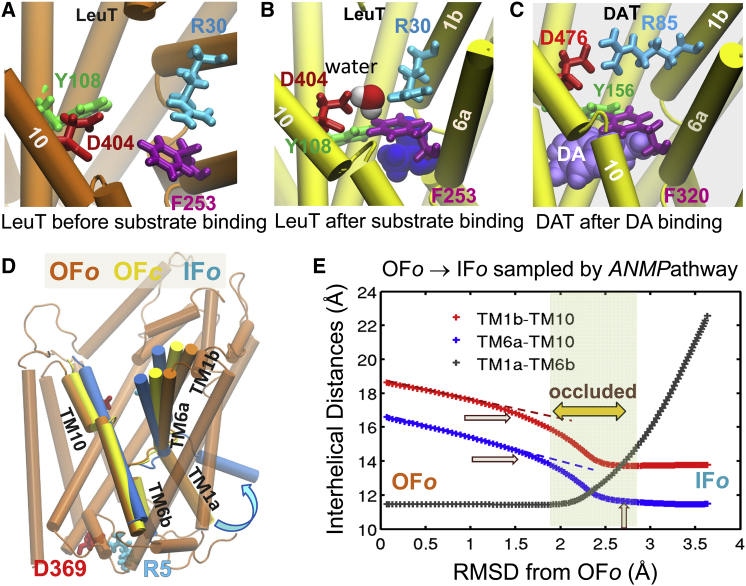
Figure 1.

Figure 1

Local and global structural changes captured by full-atomic and coarse-grained structure-based computations. (A and B) Closure of the extracellular (EC) gate after substrate binding, observed in MD simulations of leucine transporter (LeuT) (23). LeuT is known to transport alanine (most efficiently), leucine, and other amino acids. Panel A displays its substrate binding site in the outward-facing, open (OF_o_) crystal structure (24), before substrate binding. The oppositely charged residues R30 and D404, originally far apart (A), closely interact in upon substrate binding (leucine, blue space filling) (B), as illustrated for the LeuT in substrate-bound outward-facing closed (OF_c_) state (25). Likewise, the two aromatic residues, Y108-F253 closely associate to form another layer further consolidating the EC gate (23). (C) MD simulations of a LeuT structural homolog, human dopamine transporter (hDAT, modeled after the OF_o_ dDAT structure (26)) show local changes in conformation upon dopamine (DA) (light violet space filling) binding (27), which closely resemble those stabilized in substrate-bound LeuT. R85-D476 and Y156-F320 serve as the EC gates in this case. Transmembrane (TM) helical segments TM1a-b, TM6a-b, and TM10 that line the binding cavity, exhibit significant structural rearrangements. (D) Global structural differences between LeuT in OF_o_ state before substrate binding (dark orange), OF_c_ state after substrate binding (yellow), and inward-facing open (IF_o_) state (blue) after substrate release to the intracellular (IC) medium (24) (E) Global structural changes observed in ENM-based simulations of OF_o_ ↔ IF_o_ transition (28). TM1b-TM10, TM6a-TM10, and TM1a-TM6b center-of-mass (COM) distances serve as metrics for probing the extent of reconfiguration. The passage over an occluded state where the transporter is closed to both EC and IC media, consistent with experimental data (25), is highlighted.

On the other hand, if one seeks to gain insights into the conformational space accessible on a global scale, ENM-based analyses turn out to be exceptionally powerful. For example, ENM-based computations help visualize the transition between the outward-facing (OF) and inward-facing (IF) states of neurotransmitter transporters (23,28) (Fig. 1, D and E), consistent with the alternating access mechanism (25,29–31). Other examples (from the past 5 years) are the transition between the open or closed conformers of enzymes in the respective ligand-free and ligand-bound forms (32), the reconfiguration between the alternative (e.g., R and T) functional forms of allosteric proteins such as hemoglobin or GroEL (33–35) (Fig. 2), the ATP-coupled conformational mechanics of motor proteins such as myosin (34,36,37), kinesin, G-actin (38), or F1-ATPase (34), the functional mechanisms of transporters (39–41) including the above illustrated OF ↔ IF transition (Figs. 1, C and D, and 3), pore opening or allosteric gating of ion channels (42–47), or the global structural changes or concerted domain rearrangements that are stabilized upon ligand/inhibitor binding by certain proteins (6,32,48–50) (Fig. 4).

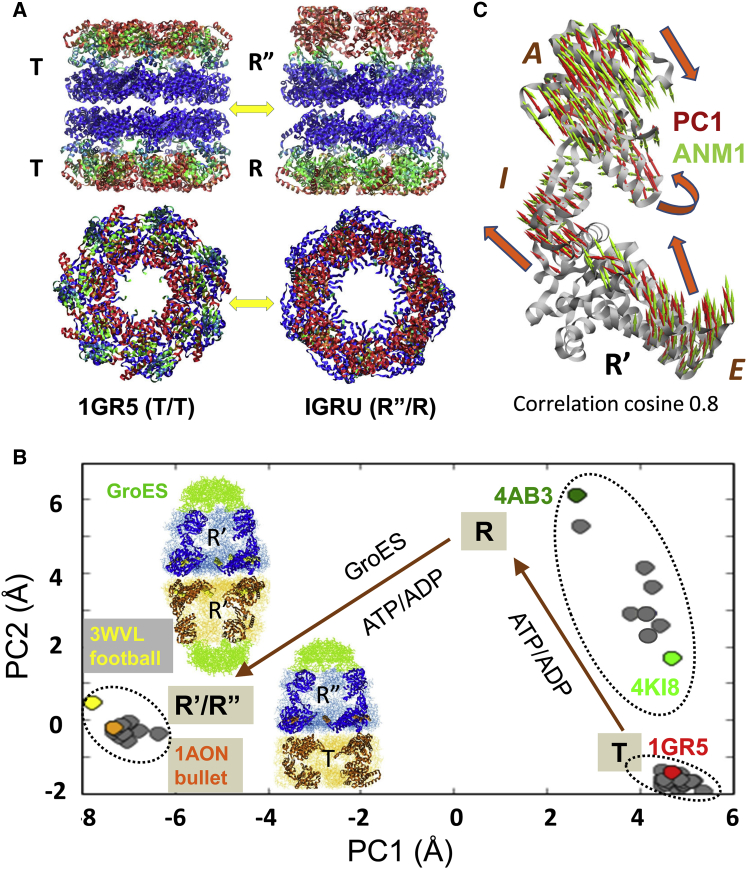
Figure 2.

Figure 2

Allosteric changes in the bacterial chaperonin complex GroEL/GroES structure are facilitated by intrinsically accessible ANM modes. GroEL consists of two heptameric rings, which assume the states (33,51): T: ATP-free; R: ATP-bound before substrate protein (SP) and co-chaperonin (GroES) binding; R′: ATP-, SP-, and GroES-bound; R″: ADP-, SP-, and GroES-bound. (A) Crystal structures of GroEL in T/T (PDB: 1GR5) and R”/R (PDB: 1GRU) states, side view (top) and top view (bottom). Residues are color-coded by experimental B-factor, as low (blue), intermediate (green), and high (red). (B) Projection of GroEL monomers on the conformational subspace spanned by the principal modes PC1 and PC2 derived from the principal component analysis (PCA) of an ensemble of 39 GroEL and GroEL/GroES structures deposited to date in the PDB. Computations are performed using ProDy (52). Examples of resolved structures, including the symmetric football-like GroEL:GroES2:ATP14 (53), are shown in inset. (C) Comparison of the directions of PC1 (red arrows) deduced from the PCA of the experimental dataset and the first ANM mode (ANM1) (green arrows) calculated using a single monomeric structure (in the R′ state). ANM1 and PC1 yield a correlation cosine of 0.8.

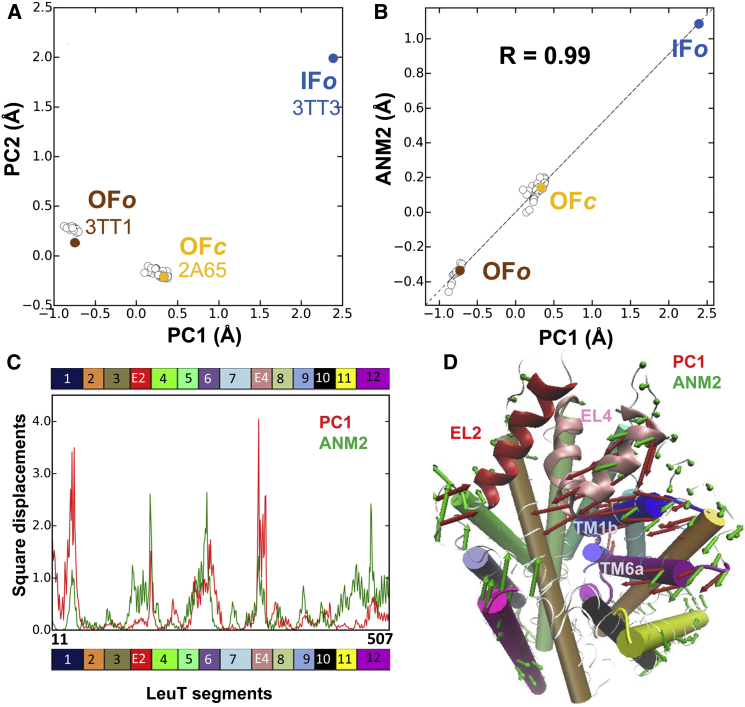
Figure 3.

Figure 3

Correlation between collective motions predicted by ANM and experimentally observed structural changes in LeuT. (A) Projection of the 50 crystal structures of LeuT monomer onto the space of conformations spanned by the principal components PC1 and PC2 shows three clusters, which broadly correspond to the crystallographically resolved LeuT structures in the OF_o_, OF_c_, and IF_o_ states. (B) Close correspondence between the structural variations along PC1 and the structural changes along ANM2. The close agreement between PC1 and ANM2 is further illustrated in (C). Here the distribution of square displacements of residues along the dominant structural difference (PC1; red) is compared with the predicted soft mode (ANM2; green). (D) Comparison of residue displacements along PC1 (red arrows) and ANM2 (green arrows). We used ProDy (52) for analysis and visualization.

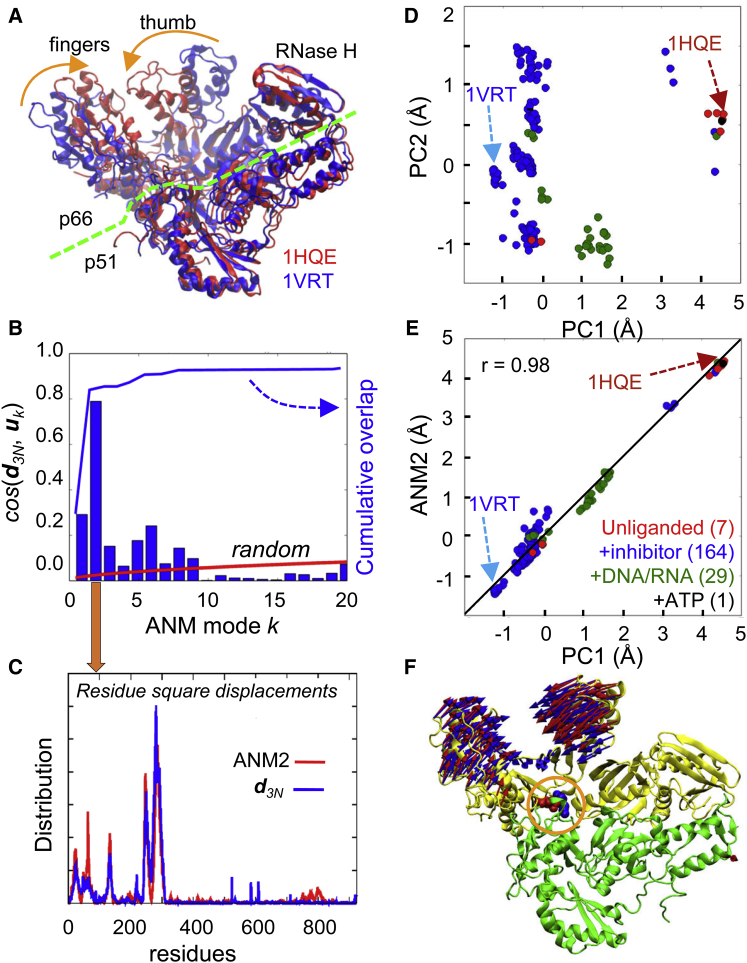
Figure 4.

Figure 4

Comparison of theoretical predictions and experimental observations for HIV-1 RT heterodimer. (A) Difference d 3N between an unliganded (1HQE) (54) and NNRTI-bound (1VRT) (56) structures. Major structural difference occurs at the fingers and thumb subdomains of the subunit p66. The green dashed line indicates the approximate boundary between p66 and p51 subunits. (B) Correlation cosines (blue bars) between d 3N and soft ANM modes (u k, for k ≤ 20) computed for 1VRT. The cumulative overlap is shown by the blue line. The red line shows the cumulative overlap expected in the absence of any orientational correlation between d 3N and ANM modes. (C) Comparison of the residue square-displacement profiles based on experiments (d 3N, blue line) and computations (ANM2, red line). (D) Projection of the ensemble of 7 unliganded (red), 164 inhibitor bound (blue), 29 DNA/RNA bound (green), and 1 ATP-bound (black) RT structures in the PDB onto the subspace of conformations spanned by the two principal components of structural differences, PC1 and PC2. (E) Close agreement between the structural changes along PC1 (experiments) and ANM2 (theory; predicted for the unliganded RT (1RTJ) (55)). (F) Comparison of the displacements along PC1 (blue arrows) and ANM2 (red arrows). The p66 and p51 subunits are colored yellow and green, respectively. Hinge residues, E138 (p51; red space filling) and K101 (p66, blue space filling), at the intersubunit interface are highlighted by the orange circle.

Are computationally predicted changes in structure meaningful? Are they functional?

Many studies in the past decade, including those cited above, have drawn attention to the physical and biological significance of computational approaches that utilize ENMs or their variants, either in NMA per se, or in hybrid methods in combination with simulation methods such as MD or Monte Carlo (MC). Structural data on proteins resolved in more than one functional state clearly support the hypothesis that computationally predicted modes of motions strongly resemble to the differences between experimentally resolved structures, and they furthermore support the view that computations based on a single structure may provide an accurate, albeit low-resolution, first description of the conformational space accessible to that structure under native state conditions.

One might argue, however, that ENMs (or NMA) predict a multitude of modes, and it may be hard to assess which ones are functionally relevant; and furthermore, given the fact that the modes represent a complete orthonormal basis set of _3N_-dimensional directional vectors, there may always be among them one or more that are relevant to the structural difference d3N = {RS1 – RS2}3N between the selected substates S1 and S2 of the same protein stabilized under different conditions. We present two major observations that refute this argument.

First, the collective modes that usually exhibit good agreement with experiments are consistently among the lowest frequency modes (6). They are the softest or the most probable modes from energetic point of view (note that the mode eigenvalue represents the curvature of the quadratic energy change along that mode coordinate, and provides a metric for the particular mode’s previous probability). The experimentally observed structural change d3N is usually observed to yield a correlation cosine of ∼0.6 or higher with one of the soft modes uk computed for S1 or S2 (e.g., 1 ≤ k ≤ 10, with mode index k = 1 referring to the softest mode) (6). Furthermore, a small subset (m ∼ tens) of softest modes usually generates a cumulative overlap Co(m) = [Σ_k_ _cos_2(d3N, uk)]1/2 (1 ≤ k ≤ m) of 0.9 or higher. For example, the change d3N between the unbound and inhibitor-bound structures of HIV-1 reverse transcriptase (RT) (Fig. 4A), yields a correlation of 0.79 with the second-softest mode (ANM2; see Movie S1 in the Supporting Material) predicted for the RT complexed with nevirapine (56), and a Co(m) = 0.9 for m = 6 (Fig. 4, B and C).

To assess the significance of these numbers, we consider the relationship Σ_k_ _cos_2(d3N, uk) = 1, where the summation is over all modes uk, 1 ≤ k ≤ 3N-6. This equality implies that the average contribution of a random mode ui would be <_cos_2(**_d_**_3N_, **_u_**_i_)> = (3N-6)-1. The correlation of 0.79 between u 2 and d3N for HIV-1 RT, for example, indicates an enhancement by a factor of f > 0.79/(3N-6)-1/2 = 42 (using N ≈ 950 for RT). Therefore, the observed correlation in RT or many other applications (6) between the easy modes of motion that are intrinsically accessible and the structural changes relevant to function (or dysfunction), is far from random: it shows the predisposition of the protein to selectively undergo those conformational changes. This also signals the evolution of the structure to favor these changes, as will be discussed below.

Secondly, we consider an even more stringent test using the complete ensemble of structures resolved (for the same protein) under different conditions/states. The PDB contains several such examples, i.e., proteins for which hundreds of structures have been resolved. Typical examples are thoroughly studied drug targets resolved in the presence of different agonists/antagonists. The idea is to analyze the space of conformations experimentally detected for each of these proteins and compare the dominant changes in structure observed in this dataset with those predicted by the ANM. This is accomplished by the following three-step analysis (32,57,58).

The benchmarking against large sets of structures provides solid, unambiguous evidence for the relevance of the ENM-predicted motions, based on a single resolved structure, to cooperative changes in conformations that proteins and their complexes and assemblies potentially undergo, while maintaining their native fold under physiological conditions. These motions are enabled by hinge sites, or key interactions at the hinge regions, usually at the interface between domains. Not surprisingly, drug-binding sites coincide with the global hinge sites in many proteins.

Future directions: bridging structural dynamics and sequence evolution

Computational studies illustrated above highlight the ability of proteins to sample a continuum of structures, rather than discrete substates, while maintaining their native fold. Clearly, different extents of deformations (usually along one of the principal modes of reconfiguration) are stabilized depending on the identity of the substrate. The ability to adapt to different extents of deformations is indeed a requirement for optimizing the interactions with substrates, endogenous or exogenous as they accomplish their activities. These observations bring us to the significance of intrinsic dynamics in evolution.

The question is: Does the sequence evolve to favor the structural dynamics that lends itself to function? A large body of studies is directed at interpreting evolutionary properties in the light of molecular structure and stability. For example, core residues tend to be conserved as they play a key role in stabilizing the fold; local packing density appears to be a major determinant of protein sequence evolution rate (59). Amino acid positions at secondary structures are usually maintained during evolution, whereas disordered regions are less conserved per amino acid position—although the composition of amino acids at disordered regions, as well as the length and position of those regions tend to be conserved (60). In addition, a multitude of methods have been developed for deriving information on coevolving pairs (or correlated mutations), and making inferences on structure based on the hypothesis that those pairs of amino acids that exhibit strong coevolutionary signals are likely to make contacts in the three-dimensional structure (61–65). A recent study (66) provides an extensive comparison of the predictive ability of several such methods for detecting coevolutionary patterns, which also confirms the utility of such methods for inferring structural contacts.

Although the relationship of structure and evolution is widely recognized, there are now increasing numbers of studies drawing attention to the functional significance of dynamics and exploring the role of structural dynamics, or structural flexibility in enabling functional events and in evolution (2,3,67–70). The reasoning behind these studies is simple: if a major incentive for sequence selection (or mutation) is to enable (or restore) function, and if the intrinsic dynamics is key to accomplishing functional changes in structure, evolutionary selection is shaped by not only the stability of the structure, but also by its inherent flexibility. The mechanical properties of the structure are indeed as important as their chemical properties—hence the term mechanochemical entities for biomolecular systems. It is widely established that chemically active sites (e.g., catalytic sites) are conserved. Why would it not be the same for the mechanically key sites, e.g., for residues enabling hinge-bending movements between cooperative domain rearrangements? Several studies now show that it is not sufficient, nor adequate, to design extremely stable structures if the goal is to mimic/capture biological functions; on the contrary, marginal stability, or intrinsic flexibility, or elasticity, is key to functionality.

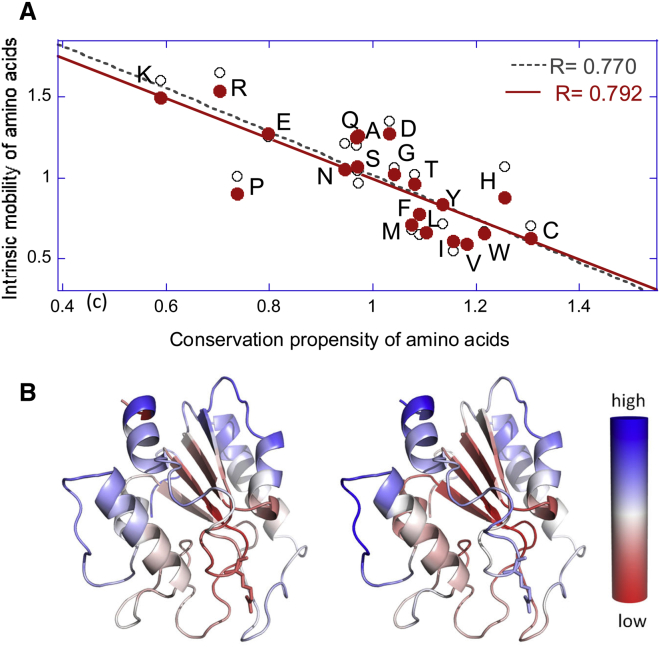
A simple comparison of the mobility scale of amino acids with their evolutionary conservation propensities yields a correlation coefficient of 0.77 (Fig. 5A). Residues that exhibit large fluctuations in their coordinates, or those enjoying high mobility under native state conditions, are sequentially variable, whereas those highly constrained (low mobility) are conserved. Note that mobility here refers to the displacements of residues, rather than their flexibility. Not all flexible residues are highly mobile. For example, glycine is very flexible and it is often located at hinge regions; the hinge regions are usually fixed in space. So, an average over all glycines (in a set of proteins) yields an intermediate mobility. Likewise, residues that tend to be buried in the core exhibit low mobilities, whereas charged residues appear to have high mobilities. The color-coded ribbon diagrams in Fig. 5B illustrate the close similarity between the conservation (left) and mobility (right) profiles of residues in an enzyme. Although the relation between sequence conservation and structural mobility may contain other effects (e.g., surface residues tend to be more mobile, in contrast to those buried in the hydrophobic core), the existence of an (anti)correlation between conservation and intrinsic flexibility cannot be overlooked. Our systematic study of 34 families of enzymes showed that the correlations become even more pronounced when focusing on the mobilities in the global modes (3). In a series of studies, the dynamic flexibility index determined from ENMs as a measure of mobility is used to understand the sequence evolution and functional enhancement (52,71–73).

Figure 5.

Figure 5

Correlation between residue conservation and conformational mobility. (A) Results from statistical analysis of the conservation propensities and intrinsic mobilities of amino acids. Both properties are expressed as enrichments relative to average behavior of all residues over a representative set of proteins (see Liu and Bahar (3) for details). Conservation is based on Shannon entropy, lower entropy indicating higher conservation; and mobility refers to ANM-predicted root-mean-square fluctuations in residue position. (B) Color-coded ribbon diagrams for human uracil-DNA glycosylase, illustrating the close similarity between Shannon entropy (left) and mobility (right) profiles of residues.

Further analysis of coevolving residues shows that many such pairs do indeed make contacts in the three-dimensional structure. A systematic analysis of coevolving pairs showed that a large fraction of coevolved residues are located close to each other (74). In particular, 80% of charge compensatory substitutions are within very close proximity (74), if not making direct contacts. However, calculations indicate other correlated pairs, which occupy distant positions in the structure. It remains to be systematically examined whether those correlated mutations originate from allosteric effects, whether they could be rationalized on the basis of long-range couplings characteristic of ENM global modes of motions. Systematic studies of allosteric proteins may shed light to the possible functional origin of those coevolving distal sites.

Author Contributions

I.B. designed the research. M.H.C., J.Y.L, C.K., and S.Z. performed the research. I.B. wrote the manuscript with input from all authors.

Acknowledgments

Support from NIH (grants R01 GM099738, P41 GM103712, and P30 DA035778) is gratefully acknowledged by I.B.

Editor: H. Jane Dyson

Footnotes

Supporting Material

Movie S1. Global motions of HIV-1 RT along ANM mode 2

This mode obtained for unliganded RT shows a close agreement (correlation coefficient of 0.82) with the principal variation in structure (PC1) deduced from the PCA of 201 HIV-1 RT structures deposited in the PDB (see also Fig. 4, E and F).

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Movie S1. Global motions of HIV-1 RT along ANM mode 2

This mode obtained for unliganded RT shows a close agreement (correlation coefficient of 0.82) with the principal variation in structure (PC1) deduced from the PCA of 201 HIV-1 RT structures deposited in the PDB (see also Fig. 4, E and F).