§25.12 Polylogarithms ‣ Related Functions ‣ Chapter 25 Zeta and Related Functions (original) (raw)
Contents
- §25.12(i) Dilogarithms
- §25.12(ii) Polylogarithms
- §25.12(iii) Fermi–Dirac and Bose–Einstein Integrals
§25.12(i) Dilogarithms
The notation Li2(z) was introduced in Lewin (1981) for a function discussed in Euler (1768) and called the _dilogarithm_in Hill (1828):
| 25.12.1 | Li2(z)≡∑n=1∞znn2, |
|---|---|
| |z | ≤1. |
| ⓘ Defines: Li2(z): dilogarithm Symbols: ≡: equals by definition,n: nonnegative integer,x: real variable andz: complex variable Keywords: definition Source: Maximon (2003, (3.1), p. 2808) A&S Ref: 27.7.2 (with z=1−x) Referenced by: §25.12(i),§25.12(i) Permalink: http://dlmf.nist.gov/25.12.E1 Encodings: TeX, pMML, png See also: Annotations for §25.12(i),§25.12 andCh.25 |
| 25.12.2 | Li2(z)=−∫0zt−1ln(1−t)dt, |
|---|---|
| z∈ℂ∖(1,∞). | |
| ⓘ Symbols: ℂ: complex plane,dx: differential of x,Li2(z): dilogarithm,∈: element of,∫: integral,lnz: principal branch of logarithm function,(a,b): open interval,∖: set subtraction,x: real variable andz: complex variable Keywords: definite integral, integral representation Source: Maximon (2003, (2.1), p. 2807) A&S Ref: 27.7.1 (is a modified form with z=1−x) Referenced by: §25.12(i) Permalink: http://dlmf.nist.gov/25.12.E2 Encodings: TeX, pMML, png See also: Annotations for §25.12(i),§25.12 andCh.25 |
Other notations and names for Li2(z) include S2(z)(Kölbig et al. (1970)), Spence function Sp(z)(’t Hooft and Veltman (1979)), and L2(z) (Maximon (2003)).
In the complex plane Li2(z) has a branch point at z=1. The principal branch has a cut along the interval [1,∞) and agrees with (25.12.1) when |z|≤1; see also §4.2(i). The remainder of the equations in this subsection apply to principal branches.
| 25.12.3 | Li2(z)+Li2(zz−1)=−12(ln(1−z))2, |
|---|---|
| z∈ℂ∖[1,∞). | |
| ⓘ Symbols: [a,b): half-closed interval,ℂ: complex plane,Li2(z): dilogarithm,∈: element of,lnz: principal branch of logarithm function,∖: set subtraction,x: real variable andz: complex variable Keywords: connection formula Source: Maximon (2003, (3.4), p. 2808) A&S Ref: 27.7.5 (is a modified form with z=1−x) Permalink: http://dlmf.nist.gov/25.12.E3 Encodings: TeX, pMML, png See also: Annotations for §25.12(i),§25.12 andCh.25 |
| 25.12.4 | Li2(z)+Li2(1z)=−16π2−12(ln(−z))2, |
|---|---|
| z∈ℂ∖[0,∞). | |
| ⓘ Symbols: π: the ratio of the circumference of a circle to its diameter,[a,b): half-closed interval,ℂ: complex plane,Li2(z): dilogarithm,∈: element of,lnz: principal branch of logarithm function,∖: set subtraction andz: complex variable Keywords: connection formula Source: Maximon (2003, (3.2), p. 2808) Referenced by: §25.12(ii) Permalink: http://dlmf.nist.gov/25.12.E4 Encodings: TeX, pMML, png See also: Annotations for §25.12(i),§25.12 andCh.25 |
| 25.12.5 | Li2(zm)=m∑k=0m−1Li2(ze2πik/m), |
|---|---|
| m=1,2,3,…, |z | <1. |
| ⓘ Symbols: π: the ratio of the circumference of a circle to its diameter,Li2(z): dilogarithm,e: base of natural logarithm,i: imaginary unit,k: nonnegative integer,m: nonnegative integer andz: complex variable Source: Maximon (2003, (3.12), p. 2809) Permalink: http://dlmf.nist.gov/25.12.E5 Encodings: TeX, pMML, png See also: Annotations for §25.12(i),§25.12 andCh.25 |
| 25.12.6 | Li2(x)+Li2(1−x)=16π2−(lnx)ln(1−x), |
|---|---|
| 0<x<1. | |
| ⓘ Symbols: π: the ratio of the circumference of a circle to its diameter,Li2(z): dilogarithm,lnz: principal branch of logarithm function andx: real variable Keywords: connection formula Source: Maximon (2003, (3.3), p. 2808) Permalink: http://dlmf.nist.gov/25.12.E6 Encodings: TeX, pMML, png See also: Annotations for §25.12(i),§25.12 andCh.25 |
When z=eiθ, 0≤θ≤2π, (25.12.1) becomes
| 25.12.7 | Li2(eiθ)=∑n=1∞cos(nθ)n2+i∑n=1∞sin(nθ)n2. |
|---|---|
The cosine series in (25.12.7) has the elementary sum
By (25.12.2)
| 25.12.9 | ∑n=1∞sin(nθ)n2=−∫0θln(2sin(12x))dx. |
|---|---|
The right-hand side is called Clausen’s integral.
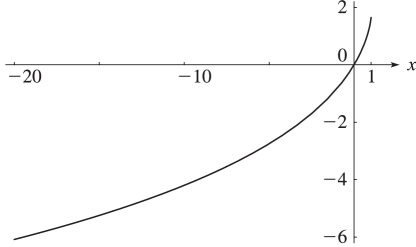
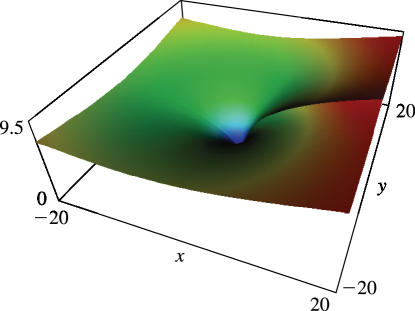
For graphics see Figures 25.12.1 and 25.12.2, and for further properties see Maximon (2003), Kirillov (1995),Lewin (1981), Nielsen (1909), and Zagier (1989).
Figure 25.12.1: Dilogarithm function Li2(x),−20≤x<1. Magnify 3D Help
Figure 25.12.2: Absolute value of the dilogarithm function |Li2(x+iy)|,−20≤x≤20,−20≤y≤20. Principal value. There is a cut along the real axis from 1 to ∞.Magnify 3D Help
§25.12(ii) Polylogarithms
For real or complex s and z the polylogarithm Lis(z) is defined by
For each fixed complex s the series defines an analytic function of z for|z|<1. The series also converges when |z|=1, provided thatℜs>1. For other values of z, Lis(z) is defined by analytic continuation.
The notation ϕ(z,s) was used for Lis(z) inTruesdell (1945) for a series treated in Jonquière (1889), hence the alternative name Jonquière’s function. The special casez=1 is the Riemann zeta function: ζ(s)=Lis(1).
Integral Representation
| 25.12.11 | Lis(z)≡zΓ(s)∫0∞xs−1ex−zdx, |
|---|---|
valid when ℜs>0 and |ph(1−z)|<π, orℜs>1 and z=1. (In the latter case (25.12.11) becomes (25.5.1)).
Further properties include
| 25.12.12 | Lis(z)=Γ(1−s)(ln1z)s−1+∑n=0∞ζ(s−n)(lnz)nn!, |
|---|---|
| s≠1,2,3,…, |lnz | <2π, |
| ⓘ Symbols: Γ(z): gamma function,ζ(s): Riemann zeta function,π: the ratio of the circumference of a circle to its diameter,!: factorial (as in n!),lnz: principal branch of logarithm function,Lis(z): polylogarithm,n: nonnegative integer,s: complex variable andz: complex variable Keywords: infinite series, series representation Source: Erdélyi et al. (1953a, (1.11.8), p. 29); take v=1 and use (25.14.3), (25.11.2) Permalink: http://dlmf.nist.gov/25.12.E12 Encodings: TeX, pMML, png See also: Annotations for §25.12(ii),§25.12(ii),§25.12 andCh.25 |
and
| 25.12.13 | Lis(z)+eπisLis(1z)=(2π)seπis/2Γ(s)ζ(1−s,lnz2πi), |
|---|---|
| z∈ℂ∖[0,∞). | |
| ⓘ Symbols: Γ(z): gamma function,ζ(s,a): Hurwitz zeta function,π: the ratio of the circumference of a circle to its diameter,[a,b): half-closed interval,ℂ: complex plane,∈: element of,e: base of natural logarithm,i: imaginary unit,lnz: principal branch of logarithm function,Lis(z): polylogarithm,∖: set subtraction,a: real or complex parameter,s: complex variable andz: complex variable Source: Erdélyi et al. (1953a, (1.11.16), p. 31); with Lis(z)=F(z,s) Referenced by: §25.12(ii),Erratum (V1.2.3) for Equation (25.12.13) Permalink: http://dlmf.nist.gov/25.12.E13 Encodings: TeX, pMML, png Modification (effective with 1.2.3): In this update we replaced e2πia by z. In this way we can remove the constraints on a and s. See also: Annotations for §25.12(ii),§25.12(ii),§25.12 andCh.25 |
When s=2 (25.12.13) becomes (25.12.4).
See also Lewin (1981), Kölbig (1986),Maximon (2003), Prudnikov et al. (1990, §§1.2 and 2.5),Prudnikov et al. (1992a, §3.3), and Prudnikov et al. (1992b, §3.3).
§25.12(iii) Fermi–Dirac and Bose–Einstein Integrals
The Fermi–Dirac and Bose–Einstein integrals are defined by
respectively. Sometimes the factor 1/Γ(s+1) is omitted. SeeCloutman (1989) and Gautschi (1993).
In terms of polylogarithms
| 25.12.16 | Fs(x) | =−Lis+1(−ex), |
|---|---|---|
| Gs(x) | =Lis+1(ex). | |
| ⓘ Symbols: e: base of natural logarithm,Lis(z): polylogarithm,x: real variable,s: complex variable,Fs(x): Fermi–Dirac integral andGs(x): Bose–Einstein integral Proof sketch: Derivable from (25.12.11), (25.12.14), (25.12.15). Permalink: http://dlmf.nist.gov/25.12.E16 Encodings: TeX, TeX, pMML, pMML, png, png See also: Annotations for §25.12(iii),§25.12 andCh.25 |
For a uniform asymptotic approximation for Fs(x) seeTemme and Olde Daalhuis (1990).