Многочлен Тейлора | это... Что такое Многочлен Тейлора? (original) (raw)

Многочлен Тейлора

Ряд Тейлора — разложение функции в бесконечную сумму степенных функций.

Ряд назван в честь английского математика Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора — его использовали ещё в XVII веке Грегори, а также Ньютон.

Ряды Тейлора применяются при аппроксимации функции многочленами. В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.

Содержание

1 Определение
2 Связанные определения
3 Свойства
- 3.1 Формула Тейлора
- 3.2 Различные формы остаточного члена
4 Ряды Маклорена некоторых функций
5 Литература
6 См. также
7 Примечания

Определение

Пусть функция f(x) бесконечно дифференцируема в некоторой окрестности точки a. Формальный ряд

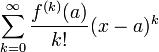
$\sum_{k=0}^\infty {f^{(k)} (a) \over k!} (x - a)^k$

называется рядом Тейлора функции f в точке a.

Связанные определения

В случае, если a = 0, этот ряд также называется рядом Макло́рена.

Свойства

Если f есть аналитическая функция, то её ряд Тейлора в любой точке a области определения f сходится к f в некоторой окрестности a.
Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности a. Например:
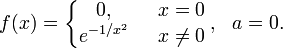
$f(x)= \left\{ \begin{matrix} 0,&\ \ x=0\\ e^{-1/x^2} &\ \ x\not=0 \end{matrix} \right.,\ \ a=0.$

Формула Тейлора

Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.

Теорема:

Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).

Различные формы остаточного члена

В форме Лагранжа:

$R_{n+1}(x) = {(x - a)^{n+1} \over (n+1)!}f^{(n+1)} [a + \theta(x - a)] \qquad p = n+1$

В форме Коши:

$R_{n+1}(x) = {(x - a)^{n+1} (1 - \theta)^n \over n!}f^{(n+1)} [a + \theta(x - a)] \qquad p = 1$

Ослабим предположения:

Пусть функция f(x) имеет n − 1 производную в некоторой окрестности точки a
И n производную в самой точке a, тогда:

$R_{n+1}(x) = o[(x - a)^n ]~$ — остаточный член в асимптотической форме (в форме Пеано)

Ряды Маклорена некоторых функций

Экспонента:

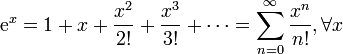
$\mathrm{e}^{x} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots = \sum^{\infin}_{n=0} \frac{x^n}{n!},\forall x$

Натуральный логарифм:

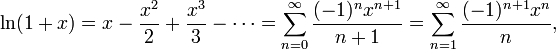$\ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \cdots = \sum^{\infin}_{n=0} \frac{(-1)^n x^{n+1}}{n+1} = \sum^{\infin}_{n=1} \frac{(- 1)^{n+1}x^n}{n},$ для всех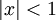 $\left| x \right| < 1$

Биномиальное разложение:

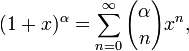$(1+x)^\alpha = \sum^{\infin}_{n=0} {\alpha \choose n} x^n,$ для всех 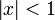$\left| x \right| < 1\quad$ и всех комплексных 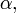$~\alpha,$ где

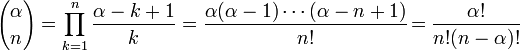
${\alpha\choose n} = \prod_{k=1}^n \frac{\alpha-k+1}k = \frac{\alpha(\alpha-1)\cdots(\alpha-n+1)}{n!}\! = \frac{\alpha!}{n!(n-\alpha)!}\!$

В частности:

Kвадратный корень:

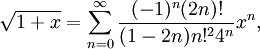$\sqrt{1+x} = \sum_{n=0}^\infty \frac{(-1)^n(2n)!}{(1-2n)n!^24^n}x^n,$ для всех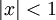 $|x|<1\!$

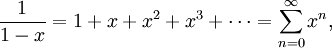$\frac{1}{1-x} = 1 + x + x^2 + x^3 + \cdots = \sum^{\infin}_{n=0} x^n,$ для всех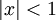 $\left| x \right| < 1$

Конечный геометрический ряд:

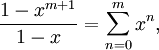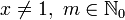
$\frac{1-x^{m + 1}}{1-x} = \sum^{m}_{n=0} x^n,$ для всех $x \not = 1,\ m\in\mathbb{N}_0\!$

Тригонометрические функции:

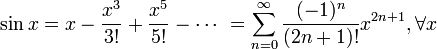
$\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots\ = \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n+1)!} x^{2n+1},\forall x$

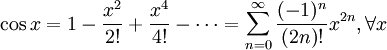
$\cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots = \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n)!} x^{2n},\forall x$

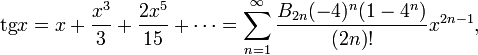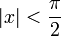
$\operatorname{tg} x = x + \frac{x^3}{3} + \frac{2 x^5}{15} + \cdots = \sum^{\infin}_{n=1} \frac{B_{2n} (-4)^n (1-4^n)}{(2n)!} x^{2n-1},$ для всех $\left| x \right| < \frac{\pi}{2}$

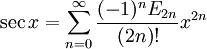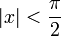
$\sec x = \sum^{\infin}_{n=0} \frac{(-1)^n E_{2n}}{(2n)!} x^{2n}$ для всех $\left| x \right| < \frac{\pi}{2}$

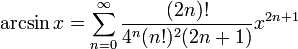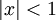
$\arcsin x = \sum^{\infin}_{n=0} \frac{(2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1}$ для всех $\left| x \right| < 1$

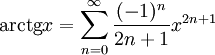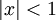
$\operatorname{arctg} x = \sum^{\infin}_{n=0} \frac{(-1)^n}{2n+1} x^{2n+1}$ для всех $\left| x \right| < 1$

Гиперболические функции:

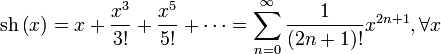
$\operatorname{sh} \left(x\right) = x + \frac{x^3}{3!} + \frac{x^5}{5!} + \cdots = \sum^{\infin}_{n=0} \frac{1}{(2n+1)!} x^{2n+1},\forall x$

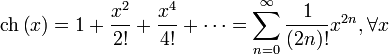
$\operatorname{ch} \left(x\right) = 1 + \frac{x^2}{2!} + \frac{x^4}{4!} + \cdots = \sum^{\infin}_{n=0} \frac{1}{(2n)!} x^{2n},\forall x$

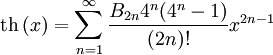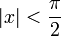
$\operatorname{th}\left(x\right) = \sum^{\infin}_{n=1} \frac{B_{2n} 4^n (4^n-1)}{(2n)!} x^{2n-1}$ для всех $\left|x\right| < \frac{\pi}{2}$

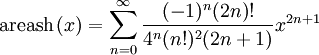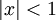
$\operatorname{areash} \left(x\right) = \sum^{\infin}_{n=0} \frac{(-1)^n (2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1}$ для всех $\left| x \right| < 1$

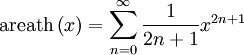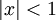
$\operatorname{areath} \left(x\right) = \sum^{\infin}_{n=0} \frac{1}{2n+1} x^{2n+1}$ для всех $\left| x \right| < 1$

Литература

В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов «Математический анализ» ч. 1, изд. 3, ред. А. Н. Тихонов, изд.: Проспект 2004.
В. Ю. Киселёв, А. С. Пяртли, Т. Ф. Калугина, Высшая математика. Первый семестр, Интерактивный компьютерный учебник.
Д. Т. Письменный «Конспект лекций по высшей математике», изд.: АЙРИС-пресс, 2002.

См. также

Ряд Фурье
Дельсарт, Жан Фридерик
Визуализация ряда Тейлора на сайте Сообщества свободного математического моделирования

Примечания

Wikimedia Foundation.2010.

Полезное

Смотреть что такое "Многочлен Тейлора" в других словарях:

Многочлен — Запрос «Полином» перенаправляется сюда; см. также другие значения. Многочлен (или полином) от n переменных это конечная формальная сумма вида , где есть набор из целых неотрицательных чисел (называется мультииндекс), число… … Википедия
Многочлен Лорана — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия
ТЕЙЛОРА МНОГОЧЛЕН — степени пдля функции f. праз дифференцируемой при х=х0 многочлен вида Значения Т. м. и его производных до порядка n включительно в точке х=х0 совпадают со значениями функции и ее соответствующих производных в той же точке: Т. м. является… … Математическая энциклопедия
ТЕЙЛОРА ФОРМУЛА — представление функции в виде суммы еи многочлена Тейлора степени п(n=0, 1, 2, . . .) и остаточного члена. Если действительная функция / одного переменного имеет ппроизводных в точке х 0, то ее Т. ф. имеет вид f(x) = Pn(x) + rn(x), где Тейлора… … Математическая энциклопедия
Теорема Тейлора — Экспоненциальная функция y = ex (сплошная красная линия) и соответствующий многочлен Тейлора четвёртого порядка (штрих пунктирная зелёная линия) вблизи начала координат … Википедия
Струя (математика) — У этого термина существуют и другие значения, см. Струя. Струя отображения на многообразии это операция, сопоставляющая каждой точке из некоторый многочлен (урезанный многочлен Тейлора в точке ). С точки зрения теории струй эти … Википедия
Расслоение струй — Струя отображения f на многообразии M это операция, сопоставляющая каждой точке x из M некоторый многочлен (урезанный многочлен Тейлора f в точке x). С точки зрения теории струй эти многочлены рассматриваются не как полиномиальные функции, а как … Википедия
Двучлен — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия
Моном — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия
Полином — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия