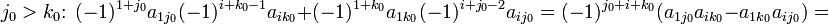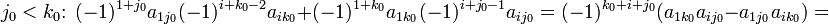Определитель матрицы | это... Что такое Определитель матрицы? (original) (raw)
Определитель матрицы
Определитель матрицы
Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (т.е. такой, у которой количество строк и столбцов равны). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.
Определитель матрицы А обозначается как: det(A), |А|, ||A|| или Δ(A).
Содержание
- 1 Определение через разложение по первой строке
- 2 Определение через перестановки
- 3 Свойства определителей
- 4 Специальные виды определителей
- 5 См. также
- 6 Литература
- 7 Ссылки
Определение через разложение по первой строке
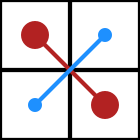
Схема расчета определителя матрицы 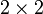 .
.
Для матрицы порядка 1 детерминантом является сам единственный элемент этой матрицы:
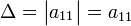
Для матрицы 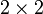 детерминант определяется как
детерминант определяется как

Для матрицы  определитель задаётся рекурсивно:
определитель задаётся рекурсивно:
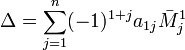 , где
, где 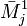 — дополнительный минор к элементу a_1_j. Эта формула называется разложением по строке.
— дополнительный минор к элементу a_1_j. Эта формула называется разложением по строке.
В частности, формула вычисления определителя матрицы 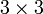 такова:
такова:
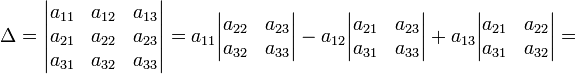
= _a_11_a_22_a_33 − _a_11_a_23_a_32 − _a_12_a_21_a_33 + _a_12_a_23_a_31 + _a_13_a_21_a_32 − _a_13_a_22_a_31
Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):
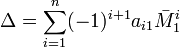
Доказательство
Пусть  .
.
Докажем, что  по индукции. Видно, что для матрицы
по индукции. Видно, что для матрицы 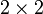 это верно:
это верно:

Предполжим, что для матрицы порядка n−1 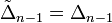 — верно.
— верно.
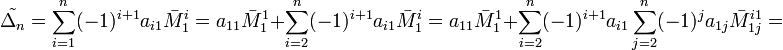

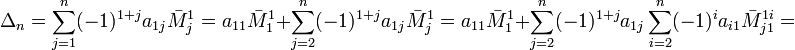
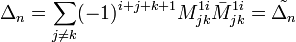 Обобщением вышеуказанных формул является разложение детерминанта по Лапласу (Теорема Лапласа), дающее возможность вычислять определитель по любым k строкам (столбцам):
Обобщением вышеуказанных формул является разложение детерминанта по Лапласу (Теорема Лапласа), дающее возможность вычислять определитель по любым k строкам (столбцам):
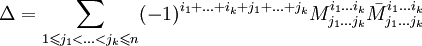
Определение через перестановки
Для матрицы  справедлива форумула:
справедлива форумула:
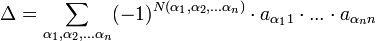 ,
,
где α1,α2,...α_n_ — перестановка порядка n, N(α1,α2...α_n_) — число инверсий в перестановке, суммирование идёт по всем возможным перестановкам порядка n. Таким образом, в определитель войдёт n! слагаемых, которые также называют "членами определителя". Важно заметить, что во многих курсах линейной алгебры это определение даётся как основное.
Свойства определителей
- Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.
- Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
- Определитель произведения матриц равен произведению их определителей.
Специальные виды определителей
- Определитель Вронского (Вронскиан)
- Определитель Вандермонда
- Определитель Грама
- Определитель Якоби (Якобиан)
См. также
Литература
- В. А. Ильин, Э. Г. Позняк Линейная алгебра, М.: Наука — Физматлит, 1999.
- Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. М.: Физматлит, 2000.
Ссылки
- Расчет определителя матрицы онлайн
Wikimedia Foundation.2010.
Полезное
Смотреть что такое "Определитель матрицы" в других словарях:
- определитель матрицы — детерминант Число, соответствующее квадратной матрице и полученное путем ее преобразования по определенному правилу. Обычное обозначение (для матрицы A) detA. Например, определитель (второго порядка) матрицы обозначается и вычисляется следующим… … Справочник технического переводчика
- Определитель матрицы, детерминант — [determinant] число, соответствующее квадратной матрице и полученное путем ее преобразования по определенному правилу. Обычное обозначение (для матрицы A) detA. Например, определитель (второго порядка) матрицы обозначается и вычисляется следующим … Экономико-математический словарь
- Определитель — У этого термина существуют и другие значения, см. Определитель (значения). Определитель (или детерминант) одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у … Википедия
- Определитель Вандермонда — Определителем Вандермонда называется определитель названный в честь французского математика Александра Теофила Вандермонда. [1] Доказательство Индукция по размеру матрицы … Википедия
- ОПРЕДЕЛИТЕЛЬ — или детерминант, в математике запись чисел в виде квадратной таблицы, в соответствие которой ставится другое число ( значение определителя). Очень часто под понятием определитель имеют в виду как значение определителя, так и форму его записи.… … Энциклопедия Кольера
- Определитель Грама — Определителем Грама (англ.) (грамианом) системы векторов в евклидовом пространстве называется определитель матрицы Грама этой системы … Википедия
- ОПРЕДЕЛИТЕЛЬ — (детерминант) квадратнойматрицы А = ||aij|| порядка n, detA многочлен … Физическая энциклопедия
- ОПРЕДЕЛИТЕЛЬ — детерминант, квадратной матрицы А=||aij|| порядка пнад ассоциативно коммутативным кольцом K с единицей 1 элемент кольца K, равный сумме всех членов вида где i1, . . ., in перестановка чисел 1, . . ., п,a t число инверсий перестановки i1,..., in.… … Математическая энциклопедия
- Определитель — детерминант, особого рода математическое выражение, встречающееся в различных областях математики. Пусть дана Матрица порядка n, т. е. квадратная таблица, составленная из п2 элементов (чисел, функций и т. п.): (каждый… … Большая советская энциклопедия
- Определитель Гессе — Гессиан функции симметрическая квадратичная форма описывающая поведение функции во втором порядке. Для функции f дважды дифференцируемой в точке или где (или … Википедия
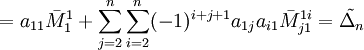
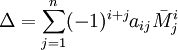
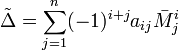 . Докажем, что
. Докажем, что 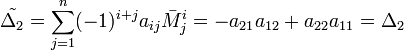 Предположим, что для матрицы порядка n−1
Предположим, что для матрицы порядка n−1  Соберём коэффициенты при
Соберём коэффициенты при 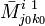 :
: 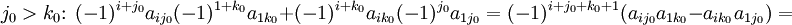

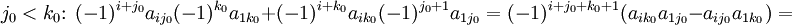
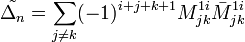
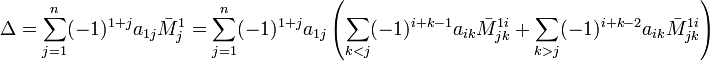 Соберём коэффициенты при
Соберём коэффициенты при