Поле Галуа | это... Что такое Поле Галуа? (original) (raw)

Поле Галуа

Поле Галуа

Конечное поле или поле Галуа — поле, состоящее из конечного числа элементов.

Конечное поле обычно обозначается 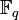\mathbb{F}_q или GF(q), где q — число элементов поля.

Простейшим примером конечного поля является 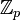\mathbb{Z}_p — кольцо вычетов по модулю простого числа.

Содержание

Свойства конечных полей

Примеры конечных полей

Построение конечных полей

Существует два варианта построения, в зависимости от количества элементов поля, которое необходимо построить:

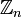Кольцо \mathbb{Z}_n вычетов по модулю n в случае простого n = p не имеет делителей нуля и является полем.

Элементы 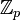\mathbb{Z}_p — числа 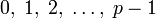0,\;1,\;2,\;\ldots,\;p-1. Операции проводятся как с обычными целыми числами с приведением по модулю p.

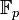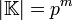Кольцо \mathbb{K}=\mathbb{F}_p[x]/\langle f(x)\rangle является полем тогда и только тогда, когда многочлен f(x) неприводим над полем \mathbb{F}_p. При этом |\mathbb{K}|=p^m, где m = deg(f). Таким образом, для построения поля из q = p n элементов достаточно отыскать многочлен степени n, неприводимый над полем 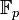\mathbb{F}_p, и определить \mathbb{K} как указано выше.

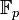Элементами поля \mathbb{K} являются все многочлены степени меньшей n с коэффициентами из \mathbb{F}_p. Операции (сложение и умножение) проводятся по модулю многочлена f(x), то есть результат соответствующей операции — это остаток от деления на f(x) с приведением коэффициентов по модулю p.

Пример построения поля GF(9)

Пусть надо построить поле GF(9) = GF(32). Для этого необходимо найти многочлен степени 2, неприводимый в 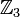\mathbb{Z}_3. Такими многочленами являются

_x_2 + 1
_x_2 + x + 2
x_2 + 2_x + 2
2_x_2 + 2
2_x_2 + x + 1
2_x_2 + 2_x_ + 1

Возьмём, например, _x_2 + 1, тогда искомое поле есть \mathrm{GF}(9)=\mathbb{Z}_3[x]/\langle x^2+1\rangle. Если вместо _x_2 + 1 взять другой многочлен, то получится новое поле, изоморфное старому.

Таблица сложения в GF(9)

\mathrm{GF}(9)=\mathbb{Z}_3[x]/\langle x^2+1\rangle

+ 0 1 2 x x + 1 x + 2 2_x_ 2_x_ + 1 2_x_ + 2
0 0 1 2 x x + 1 x + 2 2_x_ 2_x_ + 1 2_x_ + 2
1 1 2 0 x + 1 x + 2 x 2_x_ + 1 2_x_ + 2 2_x_
2 2 0 1 x + 2 x x + 1 2_x_ + 2 2_x_ 2_x_ + 1
x x x + 1 x + 2 2_x_ 2_x_ + 1 2_x_ + 2 0 1 2
x + 1 x + 1 x + 2 x 2_x_ + 1 2_x_ + 2 2_x_ 1 2 0
x + 2 x + 2 x x + 1 2_x_ + 2 2_x_ 2_x_ + 1 2 0 1
2_x_ 2_x_ 2_x_ + 1 2_x_ + 2 0 1 2 x x + 1 x + 2
2_x_ + 1 2_x_ + 1 2_x_ + 2 2_x_ 1 2 0 x + 1 x + 2 x
2_x_ + 2 2_x_ + 2 2_x_ 2_x_ + 1 2 0 1 x + 2 x x + 1

Таблица умножения в GF(9)

\mathrm{GF}(9)=\mathbb{Z}_3[x]/\langle x^2+1\rangle

× 0 1 2 x x + 1 x + 2 2_x_ 2_x_ + 1 2_x_ + 2
0 0 0 0 0 0 0 0 0 0
1 0 1 2 x x + 1 x + 2 2_x_ 2_x_ + 1 2_x_ + 2
2 0 2 1 2_x_ 2_x_ + 2 2_x_ + 1 x x + 2 x + 1
x 0 x 2_x_ 2 x + 2 2_x_ + 2 1 x + 1 2_x_ + 1
x + 1 0 x + 1 2_x_ + 2 x + 2 2_x_ 1 2_x_ + 1 2 x
x + 2 0 x + 2 2_x_ + 1 2_x_ + 2 1 x x + 1 2_x_ 2
2_x_ 0 2_x_ x 1 2_x_ + 1 x + 1 2 2_x_ + 2 x + 2
2_x_ + 1 0 2_x_ + 1 x + 2 x + 1 2 2_x_ 2_x_ + 2 x 1
2_x_ + 2 0 2_x_ + 2 x + 1 2_x_ + 1 x 2 x + 2 1 2_x_

Литература

См. также

Wikimedia Foundation.2010.

Полезное

Смотреть что такое "Поле Галуа" в других словарях: