E (число) | это... Что такое E (число)? (original) (raw)
e (число)
Область под графиком y = 1/x на интервале 1 ≤ x ≤ e равна 1 .
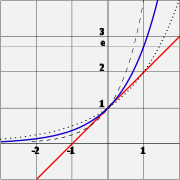
e — это некоторое число a, такое, что значение производной (наклон линии тангенса) показательной функции f (x) = ax (синяя кривая) в точке x = 0 равно 1 (красная линия). Для сравнения показаны функция 2_x_ (точечная кривая) и 4_x_ (пунктирная кривая); тангенс линии наклона которых не равен 1
e — математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e». Численное значение[1]:
e = 2,718 281 828 459 045 235 360 287 471 352 662 497 757… (последовательность A001113 в OEIS)
Число e играет важную роль в дифференциальном и интегральном исчислении, а также многих других разделах математики.
Содержание
- 1 Способы определения
- 2 Свойства
- 3 История
- 4 Мнемоника
- 5 Доказательство иррациональности
- 6 Интересные факты
- 7 См. также
- 8 Примечания
- 9 Ссылки
Способы определения
Число e может быть определено несколькими способами.
Свойства
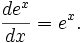
Данное свойство играет важную роль в решении дифференциальных уравнений. Так, например, единственным решением дифференциального уравнения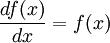 является функция
является функция 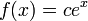 , где c — произвольная константа.
, где c — произвольная константа.- Число e иррационально и даже трансцендентно. Это первое число, которое не было выведено как трансцендентное специально, его трансцендентность была доказана только в 1873 году Шарлем Эрмитом. Предполагается, что e — нормальное число, то есть вероятность появления разных цифр в его записи одинакова.
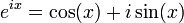 , см. формула Эйлера, в частности
, см. формула Эйлера, в частности - Ещё одна формула, связывающая числа е и π, т. н. «интеграл Пуассона» или «интеграл Гаусса»
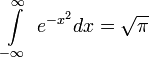
- Для любого комплексного числа z верны следующие равенства:
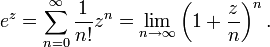
- Число e разлагается в бесконечную цепную дробь следующим образом:
![e = [2; \;1, 2, 1, \;1, 4, 1, \;1, 6, 1, \;1, 8, 1, \;1, 10, 1, \ldots] \,](http://dic.academic.ru/pictures/wiki/files/49/1571979fe5689176306c95848b75a781.png) , то есть
, то есть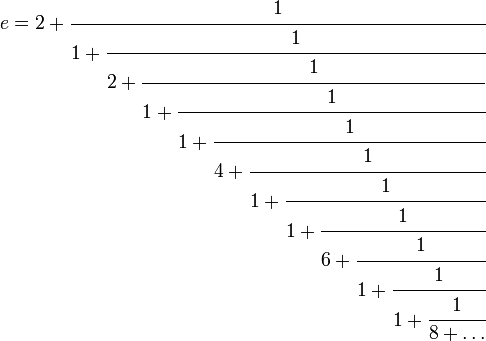
![e = \lim_{n\to\infty} \frac{n}{\sqrt[n]{n!}}.](http://dic.academic.ru/pictures/wiki/files/57/9c678d256067a90ef02d482bac3daa8f.png)
- Представление Каталана:
![e=2\cdot\sqrt{\frac{4}{3}}\cdot\sqrt[4]{\frac{6\cdot 8}{5\cdot 7}}\cdot\sqrt[8]{\frac{10\cdot 12\cdot 14\cdot 16}{9\cdot 11\cdot 13\cdot 15}}\cdots](http://dic.academic.ru/pictures/wiki/files/48/0801eaa1ae197d9777b780ea6902e619.png)
История
Данное число иногда называют неперовым в честь шотландского учёного Непера, автора работы «Описание удивительной таблицы логарифмов» (1614 год). Однако это название не совсем корректно, так как у него логарифм числа x был равен 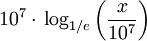 .
.
Впервые константа негласно присутствует в приложении к переводу на английский язык вышеупомянутой работы Непера, опубликованному в 1618 году. Негласно, потому что там содержится только таблица натуральных логарифмов, определённых из кинематических соображений, сама же константа не присутствует (см.: Непер).
Предполагается, что автором таблицы был английский математик Отред.
Саму же константу впервые вычислил швейцарский математик Бернулли при анализе следующего предела:
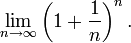
Первое известное использование этой константы, где она обозначалась буквой b, встречается в письмах Лейбница Гюйгенсу, 1690—1691 годы.
Букву e начал использовать Эйлер в 1727 году, а первой публикацией с этой буквой была его работа «Механика, или Наука о движении, изложенная аналитически» 1736 год. Соответственно, e обычно называют числом Эйлера. Хотя впоследствии некоторые учёные использовали букву c, буква e применялась чаще и в наши дни является стандартным обозначением.
Почему была выбрана именно буква e, точно неизвестно. Возможно, это связано с тем, что с неё начинается слово exponential («показательный», «экспоненциальный»). Другое предположение заключается в том, что буквы a, b, c и d уже довольно широко использовались в иных целях, и e была первой «свободной» буквой. Неправдоподобно предположение, что Эйлер выбрал e как первую букву в своей фамилии (нем. Euler).
Мнемоника
- Приблизительное значение зашифровано в: «Мы порхали и блистали, но застряли в перевале; не признали наши крали авторалли» (нужно выписать подряд цифры, выражающие число букв в словах следующего стишка, и поставить запятую после первого знака)
- Запомнить как 2,7 и повторяющиеся 18, 28, 18, 28.
- Мнемоническое правило: два и семь, далее два раза год рождения Льва Толстого (1828), затем углы равнобедренного прямоугольного треугольника (45, 90 и 45 градусов). Стихотворная мнемофраза, иллюстрирующая часть этого правила: «Экспоненту помнить способ есть простой: две и семь десятых, дважды Лев Толстой»
- Цифры 45, 90 и 45 можно запоминать как «год победы над фашистской Германией, затем дважды этот год и снова он»
- Правила e связывается с президентом США Эндрю Джексоном: 2 — столько раз избирался, 7 — он был седьмым президентом США, 1828 — год его избрания, повторяется дважды, поскольку Джексон дважды избирался. Затем — опять-таки равнобедренный прямоугольный треугольник.
- С точностью до трёх знаков после запятой через «число дьявола»: нужно разделить 666 на число, составленное из цифр 6 − 4, 6 − 2, 6 − 1 (три шестёрки, из которых в обратном порядке удаляются три первые степени двойки):
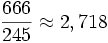 .
. - Запоминание e как
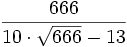 .
. - Грубое (с точностью до 0,001), но красивое приближение полагает e равным
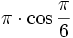 . Совсем грубое (с точностью 0,01) приближение даётся выражением
. Совсем грубое (с точностью 0,01) приближение даётся выражением 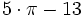 .
. - «Правило Боинга»:
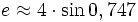 даёт неплохую точность 0,0005.
даёт неплохую точность 0,0005. - Стишки:
Два и семь, восемнадцать,
Двадцать восемь, восемнадцать,
Двадцать восемь, сорок пять,
Девяносто, сорок пять.
Доказательство иррациональности
Предположим, что  рационально. Тогда
рационально. Тогда 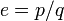 , где
, где 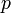 — целое, а
— целое, а 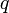 — натуральное и больше 1, т.к.
— натуральное и больше 1, т.к.  — не целое. Следовательно
— не целое. Следовательно
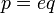
Умножая обе части уравнения на 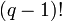 , получаем
, получаем
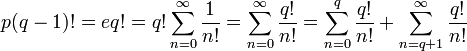
Переносим 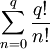 в левую часть:
в левую часть:
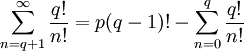
Все слагаемые правой части целые, следовательно:
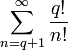 — целое
— целое
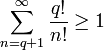
Но с другой стороны
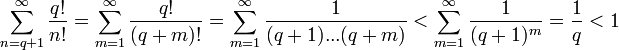
Получаем противоречие.
Интересные факты
- В IPO компании Google в 2004 году было объявлено о намерении компании увеличить свою прибыль на 2 718 281 828 долларов. Заявленное число представляет собой первые 10 цифр известной математической константы.
- В языках программирования символу e в экспоненциальной записи чисел соответствует число 10, а не Эйлерово число. Это связано с историей создания и использования языка FORTRAN для математических вычислений[2]:
Я начал программировать в 1960 году на FORTRAN II, используя компьютер IBM 1620. В то время, в 60-е и 70-е годы, FORTRAN использовал только заглавные буквы. Возможно, это произошло потому, что большинство старых устройств ввода были телетайпами, работавшими с 5-битовым кодом Бодо, который не поддерживал строчные буквы. Буква E в экспоненциальной записи тоже была заглавной и не смешивалась с основанием натурального логарифма e, которое всегда записывается маленькой буквой. Символ E просто выражал экспоненциальный характер, то есть обозначал основание системы — обычно таким было 10. В те годы программисты широко использовали восьмеричную систему. И хотя я не замечал такого, но если бы я увидел восьмеричное число в экспоненциальной форме, я бы предположил, что имеется в виду основание 8. Первый раз я встретился с использованием маленькой e в экспоненциальной записи в конце 70-х годов, и это было очень неудобно. Проблемы появились потом, когда строчные буквы по инерции перешли в FORTRAN. У нас существовали все нужные функции для действий с натуральными логарифмами, но все они записывались прописными буквами.
Например, записи 7.38e-43 соответствует число 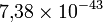 , а не
, а не 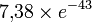 .
.
См. также
Примечания
- ↑ 2 миллиона цифр после запятой
- ↑ Эккель Б. Философия Java = Thinking in Java. — 4-е изд. — СПб.: Питер, 2009. — С. 84. — (Библиотека программиста). — ISBN 978-5-388-00003-3
Ссылки
- История числа e(англ.)
- e for 2.71828…(англ.) (история и правило Джексона)
- Горобец, Борис Соломонович. Мировые константы в основных законах физики и физиологии // Наука и жизнь. — 2004. — № 2. — статья с примерами физического смысла констант π и e
| Числа с собственными именами | |
|---|---|
| Вещественные | Пи • Золотое сечение • Серебряное сечение • Число Скьюза • e (число Эйлера) |
| Натуральные | Чёртова дюжина • Число зверя • Число Рамануджана — Харди |
| Степени десяти | Мириада • Гугол • Асанкхейя • Гуголплекс |
| Степени тысячи | Тысяча • Миллион • Миллиард • Биллион • Триллион … • … Центиллион • Зиллион |
| Степени двенадцати | Дюжина • Гросс • Масса |
Wikimedia Foundation.2010.