Математическое программирование | это... Что такое Математическое программирование? (original) (raw)

Математическое программирование

Математическое программирование — математическая дисциплина, изучающая теорию и методы решения задач о нахождении экстремумов функций на множествах конечномерного векторного пространства, определяемых линейными и нелинейными ограничениями (равенствами и неравенствами).

Формально, задача математического программирования формулируется так:

Найти 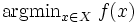\operatorname{argmin}_{x\in X}\; f(x)

В зависимости от природы множества X задачи математического программирования классифицируются как:

Кроме того, разделами математического программирования являются параметрическое программирование, динамическое программирование и стохастическое программирование. Математическое программирование используется при решении оптимизационных задач исследования операций.

Способ нахождения экстремума полностью определяется классом задачи. Но перед тем, как получить математическую модель, нужно выполнить 4 этапа моделирования:

История

Задачи линейного программирования были первыми, подробно изученными задачами поиска экстремума функций при наличии ограничений типа неравенств. В 1820 г. Ж. Фурье и затем в 1947 г. Дж. Данциг предложил метод направленного перебора смежных вершин в направлении возрастания целевой функции — симплекс-метод, ставший основным при решении задач линейного программирования.

Присутствие в названии дисциплины термина «программирование» объясняется тем, что первые исследования и первые приложения линейных оптимизационных задач были в сфере экономики, так как в английском языке слово «programming» означает планирование, составление планов или программ. Вполне естественно, что терминология отражает тесную связь, существующую между математической постановкой задачи и её экономической интерпретацией (изучение оптимальной экономической программы). Термин «линейное программирование» был предложен Дж. Данцигом в 1949 г. для изучения теоретических и алгоритмических задач, связанных с оптимизацией линейных функций при линейных ограничениях. Поэтому наименование «Математическое программирование» связано с тем, что целью решения задач является выбор оптимальной программы действий.

Выделение класса экстремальных задач, определяемых линейным функционалом на множестве, задаваемом линейными ограничениями, следует отнести к 30-м годам ХХ столетия. Одними из первых, исследовавшими в общей форме задачи линейного программирования, были: Джон фон Нейман, знаменитый математик и физик, доказавший основную теорему о матричных играх и изучивший экономическую модель, носящую его имя; советский академик, лауреат Нобелевской премии (1975 г.) Л. В. Канторович, сформулировавший ряд задач линейного программирования и предложивший (1939 г.) метод их решения (метод разрешающих множителей), незначительно отличающийся от симплекс-метода.

В 1931 г. венгерский математик Б. Эгервари рассмотрел математическую постановку и решил задачу линейного программирования, имеющую название «проблема выбора», метод решения получил название «венгерского метода».

Л. В. Канторовичем совместно с М. К. Гавуриным в 1949 г разработан метод потенциалов, который применяется при решении транспортных задач. В последующих работах Л. В. Канторовича, В. С. Немчинова, В. В. Новожилова, А. Л. Лурье, А. Брудно, А. Г. Аганбегяна, Д. Б. Юдина, Е. Г. Гольштейна и других математиков и экономистов получили дальнейшее развитие как математическая теория линейного и нелинейного программирования, так и приложение её методов к исследованию различных экономических проблем. Методам линейного программирования посвящено много работ зарубежных ученых. В 1941 г. Ф. Л. Хитчкок поставил транспортную задачу. Основной метод решения задач линейного программирования — симплекс-метод — был опубликован в 1949 г Дж. Данцигом. Дальнейшее развитие методы линейного и нелинейного программирования получили в работах Г. Куна (англ.), А. Таккера (англ.), Гасса (Gass S. I.), Чарнеса (Charnes A.), Била (Beale E. M.) и др.

Одновременно с развитием линейного программирования большое внимание уделялось задачам нелинейного программирования, в которых либо целевая функция, либо ограничения, либо то и другое нелинейны. В 1951 г была опубликована работа Куна и Таккера, в которой приведены необходимые и достаточные условия оптимальности для решения задач нелинейного программирования. Эта работа послужила основой для последующих исследований в этой области.

Начиная с 1955 г опубликовано много работ, посвященных квадратическому программированию (работы Била, Э. Баранкина (Barankin E.) и Дорфмана (Dorfman R.), Франка (Frank M.) и Вольфа (Wolfe P.), Г. Марковица и др.). В работах Денниса (Dennis J. B.), Розена (Rosen J. B.) и Зонтендейка (Zontendijk G.) разработаны градиентные методы решения задач нелинейного программирования.

В настоящее время для эффективного применения методов математического программирования и решения задач на компьютерах разработаны алгебраические языки моделирования, представителями которыми являются AMPL и LINGO.

Литература

Методы оптимизации
Одномерные Метод золотого сечения • Метод деления пополам • Метод дихотомии • Метод парабол • Метод равномерного поиска (перебора) • Метод равномерного блочного поиска • Метод троичного поиска
Прямые методы Метод Гаусса • Метод Нелдера — Мида • Метод конфигураций • Метод Розенброка • Метод сопряжённых направлений • Метод Хука — Дживса
Первого порядка Градиентный спуск • Метод покоординатного спуска • Метод сопряжённых градиентов
Второго порядка Метод Ньютона • Метод Ньютона-Рафсона
Стохастические Дифференциальная эволюция • Имитация отжига
Методы линейного программирования Метод эллипсоидов • Симплекс-метод • Метод потенциалов

Wikimedia Foundation.2010.