Правильные многомерные многогранники | это... Что такое Правильные многомерные многогранники? (original) (raw)

Правильный _n_-мерный многогранник — многогранники _n_-мерного евклидова пространства, которые являются наиболее симметричными в некотором смысле. Правильные трёхмерные многогранники называются также платоновыми телами.

Содержание

Определение

Флагом _n_-мерного многогранника P называется набор его граней F=(F_0,F_1,\dots,F_{n-1}), где F_i есть i-мерная грань многогранника Р, причем F_i \subseteq F_{n-1} для i= 1, 2,\dots,n-1.

Правильный _n_-мерный многогранник — это выпуклый _n_-мерный многогранник P, у которого для любых двух его флагов F и F' найдётся движение P, переводящее F в F'.

Классификация

n = 4

Существует 6 правильных четырёхмерных многогранников:

Ниже приведены изображения стереографических проекций правильных четырёхмерных многогранников в трёхмерное пространство:

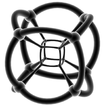Stereographic polytope 5cell.png Stereographic polytope 8cell.png Stereographic polytope 16cell.png Stereographic polytope 24cell.png Stereographic polytope 120cell.png Stereographic polytope 600cell.png

n ≥ 5

В каждой размерности n ≥ 5 существует по 3 многогранника:

Геометрические свойства

Углы

Двугранный угол между смежными гранями правильного многомерного многогранника задаётся формулой:

\sin\ {\frac{T_N}{2}}=\frac{\cos\ \frac{180^0}{W_{N-1}}}{\cos\ \frac{T_{N-1}}{2}} ;

W_{N-1}T_{N-1}\leqslant 360^0;W_{N-1}\geqslant 3 ;

Где T_N — угол между смежными гранями правильного N-мерного многогранника,T_{N-1} -угол грани, W_{N-1}-натуральное число, параметр, от которого зависит конструкция многогранника (Символ Шлефли).

Радиусы, объёмы

Радиус вписанной N-мерной сферы r_N=r_{N-1}tg\ {\frac{T_N}{2}}, где r_{N-1}радиус вписанной (N-1)-мерной сферы грани.

Объем N-мерного многогранника V_N=\frac{1}{N}V_{N-1}A_{N-1}r_N, гдеV_{N-1}объем (N-1)-мерной грани,A_{N-1}количество (N-1)-мерных граней.

Cоставление мозаики, мощение

n = 4

n ≥ 5

См. также

Ссылки

Просмотр этого шаблона Многогранники
Правильные (Платоновы тела) Трёхмерные Правильный тетраэдр • Куб • Октаэдр • Додекаэдр • Икосаэдр Четырёхмерные 6 правильных многогранников Большей размерности N-мерный куб • N-мерный октаэдр • N-мерный тетраэдр
Звёздчатый додекаэдр • Звёздчатый икосододекаэдр • Звёздчатый икосаэдр • Звёздчатый многогранник • Звёздчатый октаэдр
Выпуклые Архимедовы тела Кубооктаэдр • Икосододекаэдр • Усечённый тетраэдр • Усечённый октаэдр • Усечённый икосаэдр • Усечённый куб • Усечённый додекаэдр • Ромбокубоктаэдр • Ромбоикосододекаэдр • Ромбоусечённый кубоктаэдр • Ромбоусечённый икосододекаэдр • Курносый куб • Курносый додекаэдр • Усечённый кубооктаэдр • Усечённый икосододекаэдр • Правильная призма • Антипризма Каталановы тела Ромбододекаэдр • Ромботриаконтаэдр • Триакистетраэдр • Тетракисгексаэдр • Пентакисдодекаэдр • Триакисоктаэдр • Триакисикосаэдр • Дельтоидальный икоситетраэдр • Дельтоидальный гексеконтаэдр •Пентагональный икоситетраэдр • Пентагональный гексеконтаэдр • Дисдакисдодекаэдр • Дисдакистриаконтаэдр Без полной пространственной симметрии Пирамида • Призма • Бипирамида • Антипризма • Зоноэдр • Параллелепипед • Ромбоэдр •Призматоид• Усечённая пирамида• Пентагондодекаэдр • Параллелоэдр
Формулы, теоремы, теории Теорема Александрова о выпуклых многогранниках • Теорема Бликера • Теорема Коши о многогранниках • Теорема Линделёфа о многограннике • Теорема Минковского о многогранниках • Теорема Сабитова • Теорема Эйлера для многогранников • Теория перекатывания многогранников • Формула Шлефли
Прочее Ортоцентрический тетраэдр • Равногранный тетраэдр • Прямоугольный параллелепипед • Группа многогранника • Двенадцатигранники • Телесный угол • Единичный куб • Изгибаемый многогранник • Развёртка • Символ Шлефли • Многомерные (N-мерный тетраэдр • Тессеракт • Пентеракт • Хексеракт • Хептеракт • Октеракт • Энтенеракт • Декеракт • Гиперкуб)